图论笔记
图的概念
图:点--边
度->有向图(入度,出度)|| 无向图(度)
自环:若一条边的两个顶点为同一顶点,则此边称作自环。
路径:从任何一个点出发,随意在图上走,走出来的序列叫路径。| 简单路径(一条路径,每个点最多只能走一次)
特殊的图
1)没有环的无向图:树-->无向,连通,无环 || n个点 n-1条边
只有无向无环:很多个树-->森林
只有连通无环(有向):(连通的DAG)/有向树
只有无向连通:。。。
2)有向图的树:外向树,内向树
外向:所有边的方向都是从根向外指
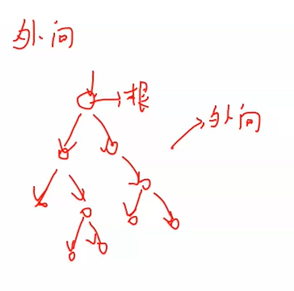
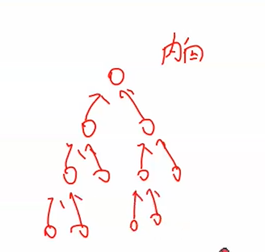
内向:所有边的方向都是从外向根的方向指
3)树的扩展:章鱼图/基环树:环上每个点连出去的部分为一棵树 || n个点的章鱼图n条边
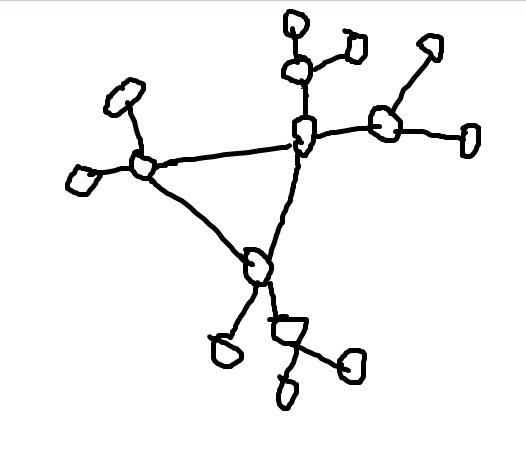
树变成章鱼图加一条边 || 章鱼图删掉环上一条边变成树
4)仙人掌图:边仙人掌,点仙人掌
边仙人掌:每条边最多在一个环上
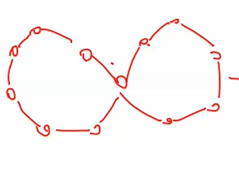
点仙人掌:每个点最多在一个环上
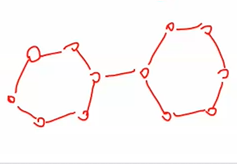
点仙人掌一定是边仙人掌
5)DAG(Directed Acyclic Graph):有向无环图
6)二分图
无向图
所有的点划为左边一部分,右边一部分,保证图当中所有的边都是从左边的一个点连到右边的一个点
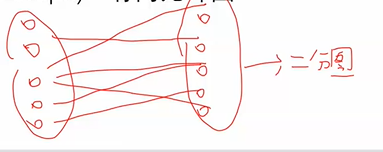
树一定是二分图
图的储存方法
邻接矩阵 ---------- 边表
优点:O(1)检查 || O(m)的内存
缺点:内存大,重边只能记一条 || 检查
最短路
单源最短路问题:求一点到所有点的最短路
多源最短路问题:求多点到所有点的最短路
最短路中的三角不等式:
dis[i][k]+dis[k][j]>=dis[i][j]
松弛操作
求最短路过程中
if dis[i][k]+k->j(k到j的长度)<dis[i][j] dis[i][j]==dis[i][k]+k->j
通过一条边来更新最短路的操作叫做松弛操作
最短路问题
1)Floyd
多源最短路算法
求任意连点之间的最短路
时间复杂度O(n3) || 空间复杂度O(n2)
处理范围n<=200~500
2)Dijkstra
单元最短路算法(前提:边权>=0)
求一个点到其他点的最短路
| dis | 1 | 2 | 3 | 4 |
| 初始化 | 0 | ∞ |
∞ |
∞ |
(1-->1的最短路是0)
3)Dijkstra+Heap

1 //By:Komorebi_03 2 #include<bits/stdc++.h> 3 using namespace std; 4 const int N = 1e6+5; 5 const int INF = 0x7fffffff; 6 int n,m,s,a,b,c,cnt,head[N]; 7 long long ans[N]; 8 bool vis[N]; 9 struct Edge{ 10 int nxt; 11 int v; 12 int w; 13 }e[N]; 14 priority_queue<pair<int,int>> q; 15 inline int read() 16 { 17 int x=0,f=1;char ch=getchar(); 18 while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();} 19 while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();} 20 return x*f; 21 } 22 23 void add(int u,int v,int w) 24 { 25 e[++cnt].v=v; 26 e[cnt].w=w; 27 e[cnt].nxt=head[u]; 28 head[u]=cnt; 29 } 30 31 void DJ(int u) 32 { 33 fill(ans,ans+N,INF); 34 q.push(make_pair(0,u)); 35 ans[u]=0; 36 while (!q.empty()) 37 { 38 int tmp=q.top().second; 39 q.pop(); 40 if(vis[tmp]) 41 continue; 42 vis[tmp]=1; 43 for (int i=head[tmp];i;i=e[i].nxt) 44 { 45 if(ans[e[i].v]>ans[tmp]+e[i].w) 46 { 47 ans[e[i].v]=ans[tmp]+e[i].w; 48 q.push(make_pair(-ans[e[i].v],e[i].v)); 49 } 50 } 51 } 52 } 53 54 int main() 55 { 56 n=read(); 57 m=read(); 58 s=read(); 59 for (int i=1;i<=m;i++) 60 { 61 a=read(); 62 b=read(); 63 c=read(); 64 add(a,b,c); 65 } 66 DJ(s); 67 for (int i=1;i<=n;i++) 68 cout<<ans[i]<<' '; 69 return 0; 70 }
4)Bellman-Ford
5)SPFA(4的一种优化
维护一个队列(?,队列里面的元素:可能改变其他点最短路的点
最坏情况下是O(nm),随机情况是O(km) k非常小的常数
负边权的题目,SPFA是你的唯一选择——zhx(((

1 //By:Komorebi_03 2 #include<bits/stdc++.h> 3 using namespace std; 4 #define int long long 5 const int INF = 2147483647; 6 const int N = 1e6+5; 7 int n,m,s,e_cnt,dis[N],vis[N],head[N]; 8 struct node{ 9 int v; 10 int w; 11 int nxt; 12 }e[N]; 13 inline int read() 14 { 15 int x=0,f=1;char ch=getchar(); 16 while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();} 17 while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();} 18 return x*f; 19 } 20 21 void add(int u,int v,int w) 22 { 23 e[++e_cnt].v=v; 24 e[e_cnt].w=w; 25 e[e_cnt].nxt=head[u]; 26 head[u]=e_cnt; 27 } 28 29 void SPFA() 30 { 31 queue<int> q; 32 for (int i=1;i<=n;i++) 33 { 34 dis[i]=INF; 35 vis[i]=0; 36 } 37 q.push(s); 38 dis[s]=0; 39 vis[s]=1; 40 while(!q.empty()) 41 { 42 int u=q.front(); 43 q.pop(); 44 vis[u]=0; 45 for (int i=head[u];i;i=e[i].nxt) 46 { 47 int v=e[i].v; 48 if(dis[v]>dis[u]+e[i].w) 49 { 50 dis[v]=dis[u]+e[i].w; 51 if(vis[v]==0) 52 { 53 vis[v]=1; 54 q.push(v); 55 } 56 } 57 } 58 } 59 } 60 61 signed main() 62 { 63 n=read(); 64 m=read(); 65 s=read(); 66 for (int i=1;i<=m;i++) 67 { 68 int u=read(); 69 int v=read(); 70 int w=read(); 71 add(u,v,w); 72 } 73 SPFA(); 74 for (int i=1;i<=n;i++) 75 { 76 if(s==i) 77 cout<<0<<" "; 78 else 79 cout<<dis[i]<<" "; 80 } 81 return 0; 82 }
例题:【APIO2013】TASKSAUTHOR - 题目 - Universal Online Judge (uoj.ac)
负环判定
1)最短路经过边数不能大于n-1
2)SPFA任何一个点入队次数不能超过n次
差分约束///
给定n个变量和m个不等式,xi-xj<=ak,求xn-x1的最大值
生成树
最小生成树,选出的n-1条边边权之和最小
1)Prim
2)Kruskal

1 #include<bits/stdc++.h> 2 using namespace std; 3 const int N = 1e6+5; 4 int n,m,x,y,z,cnt,sum,ans,fa[N]; 5 bool f=false; 6 struct node{ 7 int u; 8 int v; 9 int w; 10 }edge[N]; 11 12 bool cmp(node a,node b) 13 { 14 return a.w<b.w; 15 } 16 17 void add(int u,int v,int w) 18 { 19 edge[++cnt].u=u; 20 edge[cnt].v=v; 21 edge[cnt].w=w; 22 } 23 24 int Find(int x) 25 { 26 if(fa[x]==x) 27 return x; 28 return fa[x]=Find(fa[x]); 29 } 30 31 void Kru() 32 { 33 sort(edge+1,edge+1+cnt,cmp); 34 for (int i=1;i<=cnt;i++) 35 { 36 int u=edge[i].u; 37 int v=edge[i].v; 38 int w=edge[i].w; 39 int r1=Find(u); 40 int r2=Find(v); 41 if(r1!=r2) 42 { 43 fa[r2]=r1; 44 sum++; 45 ans+=w; 46 } 47 if(sum==n-1) 48 { 49 f=true; 50 break; 51 } 52 } 53 } 54 55 int main() 56 { 57 scanf("%d%d",&n,&m); 58 for (int i=1;i<=n;i++) 59 fa[i]=i; 60 for (int i=1;i<=m;i++) 61 { 62 scanf("%d%d%d",&x,&y,&z); 63 add(x,y,z); 64 } 65 Kru(); 66 if(f) 67 cout<<ans<<'\n'; 68 else 69 cout<<"orz"<<'\n'; 70 return 0; 71 }
强连通分量
有向图 G 强连通是指,G 中任意两个结点连通。
1)Tarjan
2)Kosaraju
3)Garbow
2-SAT
n个变量,每个变量只有两种取值(true || false)
m个表达式:xa op xb == c
问是否存一组解x1,x2,x3 . . .xn使得所有表达式成立
常用方法:Tarjan SCC 缩点

 ***********************************************************************************************************************************************************************************************************************************************************************************************************************************************************************************************************
***********************************************************************************************************************************************************************************************************************************************************************************************************************************************************************************************************


 浙公网安备 33010602011771号
浙公网安备 33010602011771号