y式dp

闫式DP分析法：

 

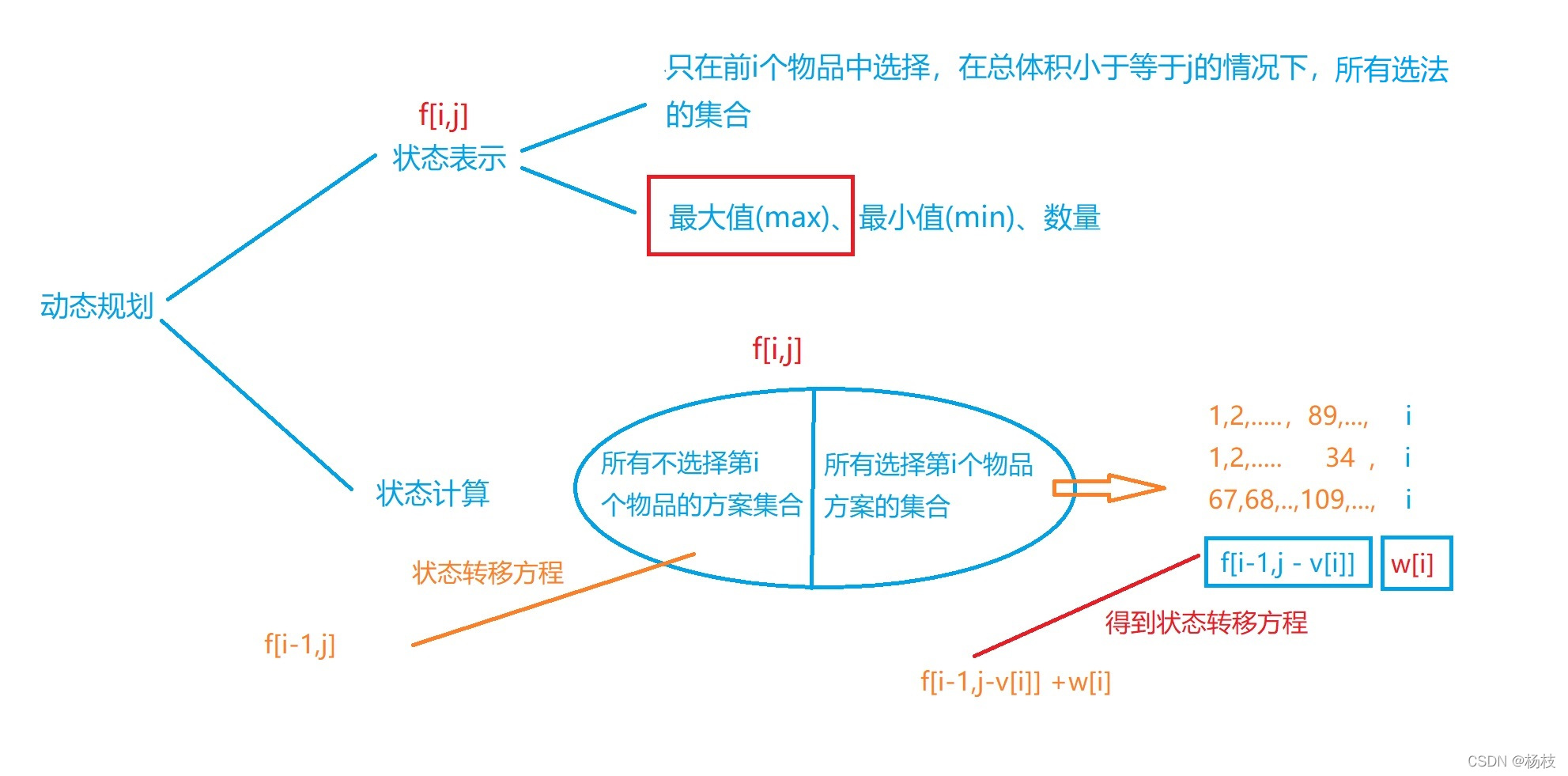
01背包
二维朴素写法
#include<iostream>
using namespace std
const int N = 1010;
int n, m;
int v[N], w[N];

int f[N][N];//在主函数外定义内存大

int main(){

cin >> n >> m;

for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];
for (int i = 1; i <= n; i ++)
for (int j = 0; j <= m; j ++ ){ // 01背包 二维 正序/逆序 更新 都可以，完全背包 二维 只能 正序更新
// for (int j = m; j >= 0; j -- ){ // 01背包 逆序 更新 也可以
f[i][j] = f[i - 1][j];
if(j>=v[i]) f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);
// 完全背包：f[i][j] = max(f[i - 1][j], f[i][j - v[i]] + w[i]);
}

cout << f[n][m] << endl;
return 0;
}
// 01背包：一维空间优化写法，进一步优化：int v[N], w[N]; ---> int v, w;
// v[i] w[i]在当层用完后就用不到了，所以用一个int型变量存储即可
优化：
#include<iostream>
using namespace std;
const int N = 1010;
int n, m;
int v, w;
int f[N]；
int main(){
cin >> n >> m;
for (int i = 1; i <= n; i ++){
for (int j = m; j >= v; j -- ) // 01背包 一维写法 只能 逆序更新
// 完全背包 一维写法 只能 正序更新：for (int j = v[i]; j <= m; j ++ )
f[j] = max(f[j], f[j - v] + w);//因j从m开始往前遍历到v[i]，所以不用if条件。
}
cout << f[m] << endl;
return 0;
}
完全背包：

 

 

#include<iostream>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];
int main(){
cin >> n >> m;
for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];
for (int i = 1; i <= n; i ++ )
for (int j = 0; j <= m; j ++ ){ // 完全背包 二维 只能 正序更新, 01背包 二维 正序/逆序 更新 都可以
if (j >= v[i]) f[i][j] = f[i - 1][j];
f[i][j] = max(f[i - 1][j], f[i][j - v[i]] + w[i]);//此状态转移方程后面可以理解选第i件物品时还可以在原包含i；
}
cout << f[n][m] << endl;
return 0;
}
优化：
#include<iostream>
using namespace std;
const int N = 1010;
int n, m;
int v, w;
int f[N];
int main(){
cin >> n >> m;
for (int i = 1; i <= n; i ++ ){ // 注意加了cin >> v >> w; 之后, 这里有个 大括号
cin >> v >> w;
for (int j = v; j <= m; j ++ ) // 完全背包 一维 只能 正序更新
// 01背包 一维 只能 逆序更新: for (int j = m; j >= v[i]; j -- )
f[j] = max(f[j], f[j - v] + w);
}
cout << f[m] << endl;
return 0;
}
区间dp：
设有 N 堆石子排成一排，其编号为 1，2，3，…，N。
每堆石子有一定的质量，可以用一个整数来描述，现在要将这 N 堆石子合并成为一堆。
每次只能合并相邻的两堆，合并的代价为这两堆石子的质量之和，合并后与这两堆石子相邻的石子将和新堆相邻，合并时由于选择的顺序不同，合并的总代价也不相同。
例如有 4 堆石子分别为 1 3 5 2， 我们可以先合并 1、2 堆，代价为 4，得到 4 5 2， 又合并 1，2 堆，代价为 9，得到 9 2 ，再合并得到 11，总代价为 4+9+11=24；
如果第二步是先合并 2，3 堆，则代价为 7，得到 4 7，最后一次合并代价为 11，总代价为 4+7+11=22。
问题是：找出一种合理的方法，使总的代价最小，输出最小代价。
输入格式
第一行一个数 N 表示石子的堆数 N。
第二行 N 个数，表示每堆石子的质量(均不超过 1000)。
输出格式
输出一个整数，表示最小代价。
数据范围
1≤N≤300
输入样例：
4
1 3 5 2
输出样例：
22

 

 

 

代码：
// 所有将[i,j]合并成一堆代价最小的方案的集合
#include<iostream>
using namespace std;
const int N=1010;
int n;
int s[N];//前缀和,前n个堆的质量和
int f[N][N];
int main()
{
int i,j;
cin>>n;
for(i=1;i<=n;i++) {cin>>s[i];s[i]+=s[i-1];}
for( int len=2;len<=n;len++)//枚举区间长度
for(int i=1;i+len-1<=n;i++)//枚举区间长度为len的方案
{
int j=i+len-1;//右端点表示
f[i][j]=1e8;
for(int k=i;k<j;k++)
f[i][j]=min(f[i][j],f[i][k]+f[k+1][j]+s[j]-s[i-1]);//状态转移方程
}
cout<<f[1][n]<<endl;
return 0;
}
4、最长子序列(集合序列问题）

给定两个长度分别为N和M的字符串A和B，求既是A的子序列又是B的子序列的字符串长度最长是多少。
输入格式
第一行包含两个整数N和M。
第二行包含一个长度为N的字符串，表示字符串A。
第三行包含一个长度为M的字符串，表示字符串B。
字符串均由小写字母构成。
输出格式
输出一个整数，表示最大长度。
数据范围
1≤N≤1000,
输入样例：
4 5
acbd
abedc
输出样例：
3

 

 

 

 

 

 

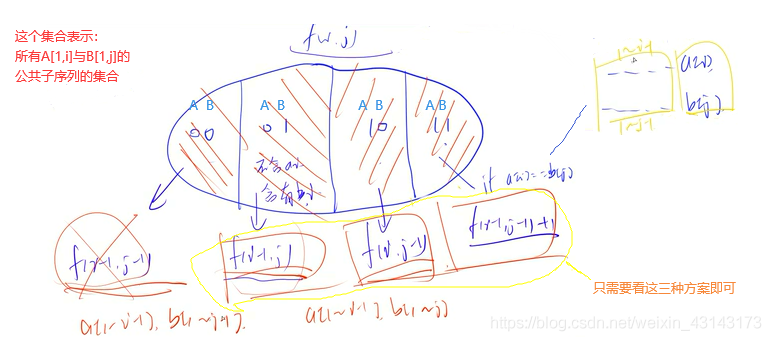
集合：所有满足a[1~i]与b[1~j]的公共子序列的集合
属性：max;#include<iostream>
using namespace std;
const int N=10000;
int n,m;
char a[N],b[N];
int f[N][N];
int main()
{ int i,j;
cin>>n>>m>>a+1>>b+1;
for(i=1;i<=n;i++)
for(j=1;j<=m;j++)
{//最后的不同点四种情况
f[i][j]=max(f[i-1][j],f[i][j-1]);//01，10，00情况对于f[i-1][j]和f[i][j-1]包含了不包含二者的情况
if(a[i]==b[j]) f[i][j]=max(f[i][j],f[i-1][j-1]+1);//11情况（包含a[i]和b[j]）
}
cout<<f[n][m]<<endl;
return 0;
}