Link-Cut-Tree入门

Link Cut Tree的主要作用是维护一个动态森林中点与点间的路径动态信息。
相比于树链剖分，Link Cut Tree能支持动态删连边，这是因为树剖用线段树来维护区间，而LCT用Splay的旋转与区间翻转的特性来维护点与点间的相对关系。
那么首先，我们需要像树剖那样，把一棵树分成若干条树链（专业术语叫“实链剖分”），以保证每一次操作的均摊复杂度为O(log n)。
剖分要满足： 一条链中不能出现两个深度相同的点，可以理解为一条链是从一个点出发向整棵树的根走若干步的路径。
注意：一个点也可以被认为是一条链。
也就是说，对于一棵树，把每一个点都认为是一条链是合法的，也是最简单的。所以对于一颗还没有进行任何操作的树，我们不妨将每个点划分成单独的链。

下面来一个具体的例子：

这里不妨假设这棵树之前进行了若干操作以至于有了这样的剖分

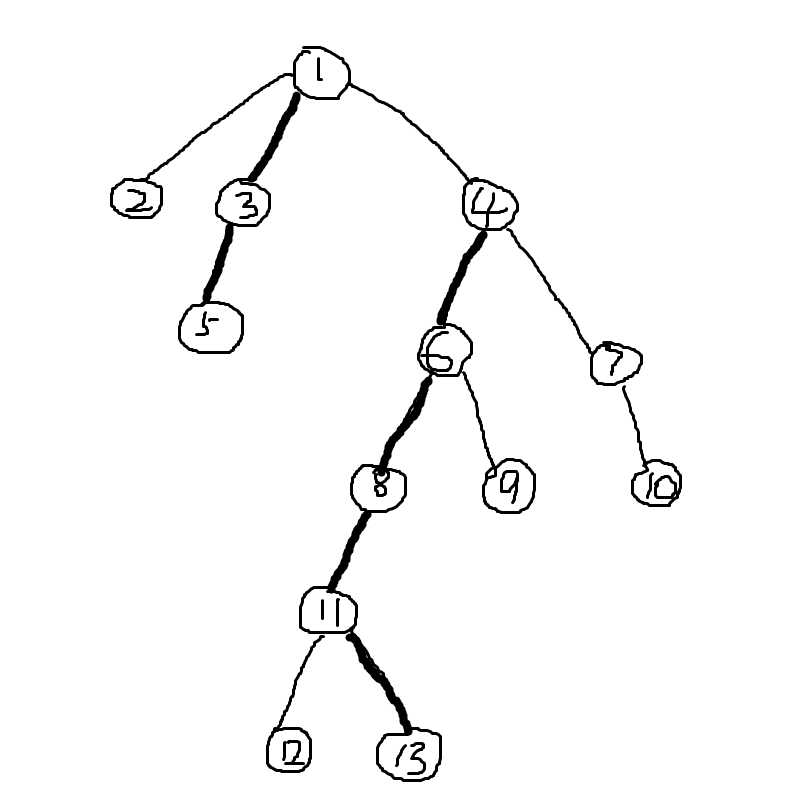
首先来考虑存一棵树的方法：对于一条链上的，把所有节点存到一个Splay当中。
比如这个例子，其中的一个Splay就长这样：

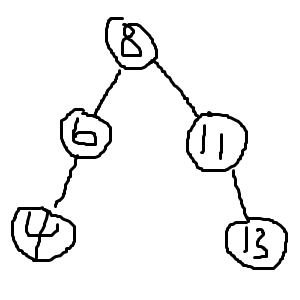
需要注意的是，这里平衡的关键字是点的深度，也就是说在左子树的都是实际树中该点的祖先，右子树的都是该点的儿子。

然后发现：在实际树中除了根节点所在的链之外，每条链的顶端都连着一个不属于自己这条链的点（也就是说一个Splay会“指向”一个点）。
那就简单了，存图的时候直接让Splay根节点的父亲指向那个点不就可以了~
下图中红线代表父亲，蓝线代表在Splay中的左右儿子：

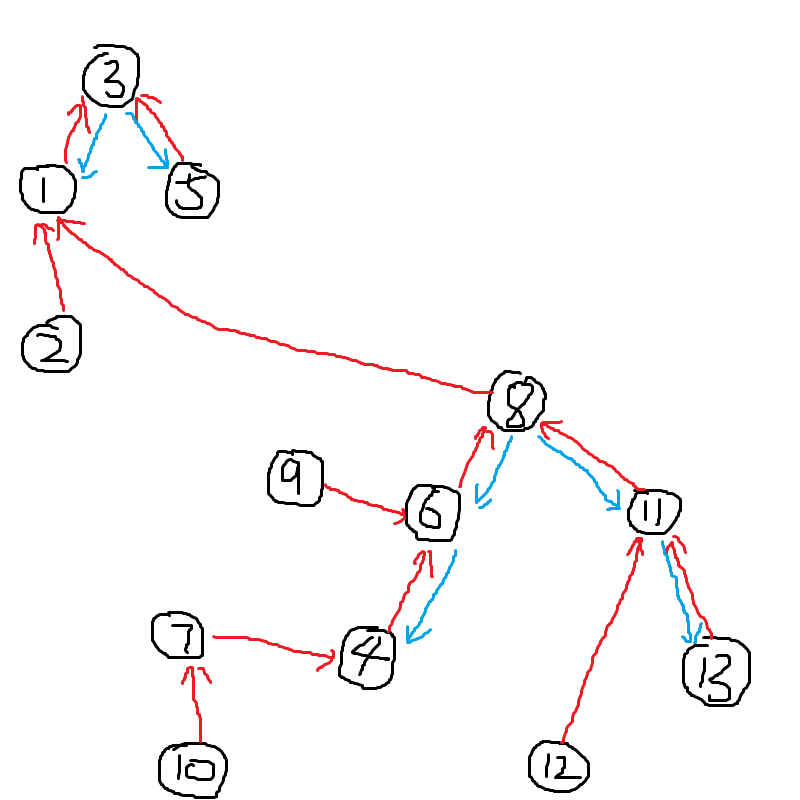
总结：

1. 一个节点所连的子节点只是该点所在Splay中的左右儿子
2. 一个节点所连的父亲有两种情况：若该点是所在Splay的根，那么指向的是原树中该链的顶端节点的父亲；若该点不是所在Splay的根，那么指向的就是它在Splay中的父亲

LCT的一个基本操作是access(x)，作用是让且仅让x到实际树根的路径上所有点在一个Splay上
就比如遇到了某个点（作为自己所在Splay的根）和父亲（也作为自己所在Splay的根）不在一个Splay上，然后要access。注意是“让且仅让”，所以必须断开父节点之前连向儿子的重边。仔细想一想，父亲在Splay中的所有右节点不都是的嘛！所以直接断开与右儿子的父子关系即可（子父关系不能断）。这是删除之前的，那么连上现在的，就是把自己直接作为父亲的右节点（刚刚空出来的）。代码就一行：

void access(int x){for(int y=0;x;y=x,x=fa[x])splay(x),son[x][1]=y,pushup(x);}

好吧还是解释一下(｡･ω･｡)：

void access(int x){
	for(int y=0;x;y=x,x=fa[x]){//y是暂时存上一次处理的Splay的根，方便直接作为父亲的右节点 
		splay(x);//先得把x旋到自己所在Splay的根，好与所有原来的重边断开父子关系 
		son[x][1]=y;//再让y成为右儿子 
		update(x);//在本题中要维护的是异或，所以update就是
		//v[x]=v[son[x][0]]^v[son[x][1]]^val[x];
		//这样x所在的整个链都异或进v[x]了（x是根节点）
	}
}

下一个操作makeroot(x)，作用是让x成为整棵树的根（也就是空出其父节点），这样做的意义会在之后的Link和Cut中体现。也只有一行：

void makeroot(int x){access(x);splay(x);rev[x]^=1;}

这个时候只access(x)和splay(x)没有意义，因为一个Splay真正连向另一个点的不是这个Splay的根，而是这个Splay中深度（关键字）最小的点，也就是从根一直往左走到头。
要想真正让x成为根还需要加个翻转左右子树的操作（别忘了在splay的时候加pushdown！），于是x没有了左儿子，成为了真正的根。

接下来终于到了关键操作Link和Cut：

inline void link(int x,int y){makeroot(x);fa[x]=y;}

刚才讲到，makeroot(x)的作用在于让x没有父节点，这样就可以添加新的父节点，也就是要合并的y。

void cut(int x,int y){
	makeroot(x);
	access(y);
	splay(y);
	//上面三句话作用是让x,y在一个Splay里，并且x是y往左走到头的点
	//可以把上面三句话封装成一个split(x,y) 
	if(son[y][0]==x&&son[x][1]==0){//如果x与y相连 
		son[y][0]=0;fa[x]=0;//断开x与y的关系 
	}
}

来一个find，用来找一个点所在树的根，这样就好判断两个点是否在一棵树里

int find(int x){
	access(x);//先让x与树根联系起来 
	splay(x);//让x成为Splay的根 
	while(son[x][0])x=son[x][0];//一直往左走，找到深度最小的点 
	return x;
}

好了，LCT的大致思想已经写的很详细了，来个板子。

【模板】Link Cut Tree

#include<bits/stdc++.h>
#define ri register int 
using namespace std;
inline int read(){
    ri f=1,x=0;register char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
    return f*x;
}
const int maxn=300010;
int n,m,val[maxn],top,son[maxn][2],fa[maxn],v[maxn],q[maxn],rev[maxn];
inline void update(int x){v[x]=v[son[x][0]]^v[son[x][1]]^val[x];}
inline void pushdown(int x){rev[son[x][0]]^=1;rev[son[x][1]]^=1;rev[x]^=1;swap(son[x][0],son[x][1]);}
inline bool isroot(int x){return son[fa[x]][0]!=x&&son[fa[x]][1]!=x;}
inline void rotate(int x){
    ri y=fa[x],z=fa[y],d=son[y][1]==x;
    if(!isroot(y))son[z][son[z][1]==y]=x;fa[x]=z;
    fa[son[y][d]=son[x][d^1]]=y;
    fa[son[x][d^1]=y]=x;
    update(y);update(x);
}
inline void splay(int x){
    top=1;q[top]=x;
    for(ri i=x;!isroot(i);i=fa[i])q[++top]=fa[i];
    for(ri i=top;i;i--)if(rev[q[i]])pushdown(q[i]);
    for(ri y=fa[x];!isroot(x);rotate(x),y=fa[x])
        if(!isroot(y))rotate((son[y][0]==x)^(son[fa[y]][0]==y)?x:y);
}
inline void access(int x){for(ri y=0;x;y=x,x=fa[x])splay(x),son[x][1]=y,update(x);}
inline void makeroot(int x){access(x);splay(x);rev[x]^=1;}
inline int find(int x){access(x);splay(x);while(son[x][0])x=son[x][0];return x;}
inline void split(int x,int y){makeroot(x);access(y);splay(y);}
inline void cut(int x,int y){split(x,y);if(son[y][0]==x&&son[x][1]==0)son[y][0]=0,fa[x]=0;}
inline void link(int x,int y){makeroot(x);fa[x]=y;}
int main(){
    n=read();m=read();for(ri i=1;i<=n;i++)v[i]=val[i]=read();
    while(m--){
        ri opt=read(),x=read(),y=read();
        if(opt==0){split(x,y);printf("%d\n",v[y]);}
        if(opt==1){if(find(x)!=find(y))link(x,y);}
        if(opt==2){if(find(x)==find(y))cut(x,y);}
        if(opt==3){access(x);splay(x);val[x]=y;update(x);}
    }
    return 0;
}