FFT入门

问题引入

对于两个多项式\(f(x)=\sum_{i=0}^{n}a_ix^i\)和\(g(x)=\sum_{j=0}^{m}b_jx^j\)，\(f(x)\cdot g(x)\)被称为\(f(x)\)和\(g(x)\) 的卷积。
很明显，设\(f(x)\cdot g(x)=\sum_{i=0}^{n+m}c_ix^i\)，那么\(c_k=\sum_{i+j=k}a_ib_j\)。如果暴力地求所有的\(c_k\)显然是\(O(n^2)\)的。所以我们需要一种更高效的方法来求卷积。

多项式的两种表示方法

1. 系数表示法：在每一个x前加上系数即可，对于一个n-1次多项式可以表示为\(A(x)=\sum_{i=0}^{n-1}a_ix^i\)。
2. 点值表示法：我们知道由n个点可以确定一个唯一的n-1次函数，可以用\((x_1,A(x_1)),\dots,(x_n,A(x_n))\)这n个点来表示一个多项式。在这种表示方法下，两个所有点横坐标取值相等的多项式相乘，只需把对应点的纵坐标相乘即可。

进入正题

FFT的多项式乘法由三部分构成：

1. 系数表示->点值表示   \(O(nlogn)\)
2. 点值相乘   \(O(n)\)
3. 点值表示->系数表示   \(O(nlogn)\)

但其实上1，3的代码是共用的，2的代码就一行，所以FFT模板代码其实很短。

开始思考

FFT的优化在哪里呢？其实在带入\(n\)个\(x\)值的过程中，让\(x_i\)与\(x_{i+\frac{n}{2}}\)产生一定联系，只用计算其中一个另一个就可以立刻知道，这样就可以节约一半的时间。然后再一层一层分治，最终就有\(O(nlogn)\)的复杂度。
当然了，代入的x可不是随便取的，傅里叶说：要取这个圆上的数

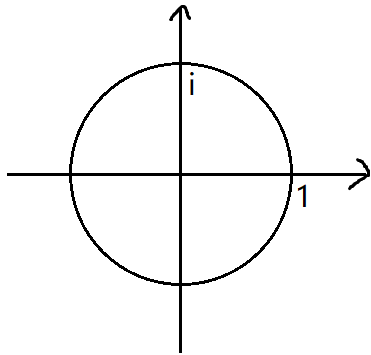
我们把形如\(z=a+bi\)（\(a,b\)均为实数）的数称为复数，其中\(a\)称为实部，\(b\)称为虚部，\(i\)称为虚数单位。可以把复数看做平面上的一个点，横坐标为实部，纵坐标为虚部。
模长：点到原点的距离，即\(\sqrt{a^2+b^2}\)
幅角：从正半轴开始以逆时针为正方向的旋转的角度
复数也可以做四则运算：

• \((a+bi)\pm(c+di)=(a\pm c)+(b\pm d)i\)
• \((a+bi)(c+di)=(ac-bd)+(bc+ad)i\)

上式经过几何推导（此处省略）后可得出，两复数相乘的几何意义是：模长相乘，幅角相加。（可以自己试验一下）
好了，那么你现在应该明白为什么傅里叶要选这个单位圆上的点了，在这个圆上的复数无论怎么相乘都逃离不了这个圆！如果均匀的选点的话，也就是说把这个圆分成n份（这里和接下来的所有n都认为是2的若干次方），第\(i\)个点与第\(i+\frac{n}{2}\)个点刚好是相对的！
这里的点有一个专业术语，叫单位根，用\(\omega_n^k\)来表示把单位圆分成n份后的第i个点所代表的复数。显然，有：

• \(\omega_n^0=\omega_n^n=1\)
• \(\omega_n^k=\omega_n^{k+an}\ (a\in Z)\)
• \(\omega_n^k=\omega_{an}^{ak}\ (a\in N^* )\)
• \(\omega_n^k+\omega_n^{k+\frac{n}{2}}=0\)

开始推式子

设待代入\(\omega_n^k\ (0\leq k<n)\)的多项式为\(A(x)=\sum_{i=0}^{n-1}a_ix^i\)
再设\(A_0(x)=\sum_{i=0}^{\frac{n}{2}-1}a_{2i}x^i\)，\(A_1(x)=\sum_{i=0}^{\frac{n}{2}-1}a_{2i+1}x^i\)
则有\(A(x)=A_0(x^2)+xA_1(x^2)\)（即按奇偶分开）
再代入\(\omega_n^k\)和\(\omega_n^{k+\frac{n}{2}}\)两个单位根，

\[\begin{aligned} A(\omega_n^k)&=A_0(\omega_n^{2k})+\omega_n^kA_1(\omega_n^{2k})&=A_0(\omega_{\frac{n}{2}}^{k})+\omega_n^kA_1(\omega_{\frac{n}{2}}^{k})\\ A(\omega_n^{k+\frac{n}{2}})&=A_0(\omega_n^{2k+n})+\omega_n^{k+\frac{n}{2}}A_1(\omega_n^{2k+n})&=A_0(\omega_{\frac{n}{2}}^{k})-\omega_n^kA_1(\omega_{\frac{n}{2}}^{k}) \end{aligned} \]

只有一个正负号的区别！于是我们再递归求出\(A_0(\omega_{\frac{n}{2}}^{k})\)和\(A_1(\omega_{\frac{n}{2}}^{k})\)，就可以\(O(nlogn)\)的系数转点值了！
如果直接把\(A(x)\)的各项系数分成两半，在递归的过程中不断转移会影响效率，所以干脆提前处理好位置，这样之后就可以像线段树一样区间合并。

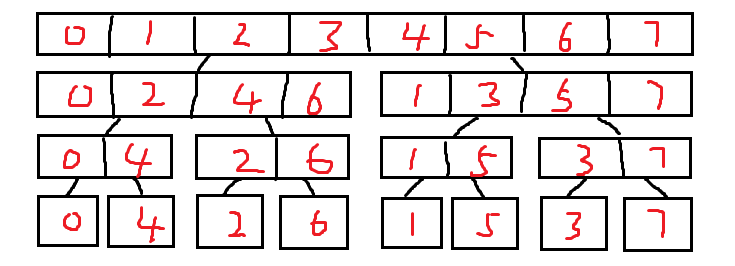
图中的数字代表原多项式的第几次项系数，不难发现，第i项系数的最终实际的位置其实在i的二进制反转位（比如1的二进制是001，反转后是100，也就是第4个）。这个预处理叫蝴蝶变换。

点值转系数

刚才的一波操作成功的在\(O(nlogn)\)的时间内将系数转为了在n个单位根处的点值。那么再用\(O(n)\)将两个点值表示的多项式相乘后，如何将新的点值表示转化成系数表示呢？这里就需要用到FFT的逆变换——IFFT。
我们设待转换的多项式为\(A(x)\)，已经知道了\(A(\omega_n^k)\)在\(k\)取\(0\)到\(n-1\)的值\(c_k\)，想要求\(A(x)\)的各项系数。
根据\(c_k\)的定义，对所有\(k\)有\(c_k=\sum_{i=0}^{n-1}a_i\omega_n^{ki}\)。我们发现对于每个\(i\)，\(a_i\)在\(A(\omega_n^k)\)中的系数是\(\omega_n^{ki}\)，那么如何从\(c_k\)中“提取出”单个的\(a_i\)呢？怎么利用单位根的对称性呢？
构造多项式\(B(x)=\sum_{i=0}^{n-1}c_ix^i\)，那么\(B(\omega_n^k)=\sum_{i=0}^{n-1}c_i\omega_n^{ki}=\sum_{i=0}^{n-1}(\sum_{j=0}^{n-1}a_j\omega_n^{ij})\omega_n^{ki}\)
括号展开后\(=\sum_{i=0}^{n-1}\sum_{j=0}^{n-1}a_j\omega_n^{(k+j)i}\)
调整顺序后\(=\sum_{j=0}^{n-1}a_j\sum_{i=0}^{n-1}\omega_n^{(k+j)i}\)
当\(k+j=0\)时，\(\omega_n^{(k+j)i}\)始终为1，所以\(a_j\)的系数为\(n\)；
当\(k+j\neq0\)时，因为\(i\)取遍了0到n-1的所有值，n又是2的次幂，所以\(a_j\)在\(B(\omega_n^k)\)中的系数为\(0\)。
所以IFFT只需把单位根反向，然后直接把\(c_k\)看做新的多项式的系数，再来一次系数转点值，求出\(B(x)\)在\(\omega_n^{-k}\)处的点值再除以n即可。

模板代码

#include <bits/stdc++.h>
#define ri register int
using namespace std;
inline int read(){
	register int f=1,x=0;register char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
	return f*x;
}
const int maxn=4000010;const double pi=acos(-1.0);
struct CP{
	double x,y;
	CP(double a=0,double b=0){x=a;y=b;}
	CP operator+(const CP &t)const{return CP(x+t.x,y+t.y);}
	CP operator-(const CP &t)const{return CP(x-t.x,y-t.y);}
	CP operator*(const CP &t)const{return CP(x*t.x-y*t.y,x*t.y+y*t.x);}
}a1[maxn],a2[maxn],ans[maxn];
int n,rev[maxn];
void fft(CP *a,int tp){
	for(ri i=0;i<n;i++)if(i<rev[i])swap(a[i],a[rev[i]]);
	for(ri mid=1;mid<n;mid<<=1){//mid:递归的两个子区间的长度
		CP n1(cos(pi/mid),tp*sin(pi/mid));//单位根
		for(ri j=0;j<n;j+=mid<<1){
			CP nk(1,0);
			for(ri k=0;k<mid;k++,nk=nk*n1){
				CP x=a[j+k],y=nk*a[j+mid+k];
				a[j+k]=x+y;a[j+mid+k]=x-y;
			}
		}
	}
}
int main(){
	ri n1=read(),n2=read(),n12=n1+n2,logn;
	for(n=1,logn=0;n<=n12;n<<=1,++logn);
	for(ri i=0;i<=n1;i++)a1[i].x=read();
	for(ri i=0;i<=n2;i++)a2[i].x=read();
	for(ri i=0;i<n;i++)rev[i]=(rev[i>>1]>>1)|((i&1)<<(logn-1));
	fft(a1,1);fft(a2,1);
	for(ri i=0;i<=n;i++)ans[i]=a1[i]*a2[i];
	fft(ans,-1);
	for(ri i=0;i<=n12;i++)printf("%d ",(int)(ans[i].x/n+0.5));
	return 0;
}