[Luogu && Codeforces] CF1030B 题解

###### # CF1030B 题解

纯数学题。
题意够清楚了，不用解释了吧。

先求出此图形四条边的函数解析式。
因为四边都是直线，所以解析式都是一次函数，按照求一次函数解析式的方法做就行了。
如图，设四边形的四个顶点分别为 \(A\)、\(B\)、\(C\)、\(D\)，四条边的解析式分别为 \(AD=f(x)\)、\(DC=g(x)\)、\(CB=h(x)\)、\(AB=i(x)\)。

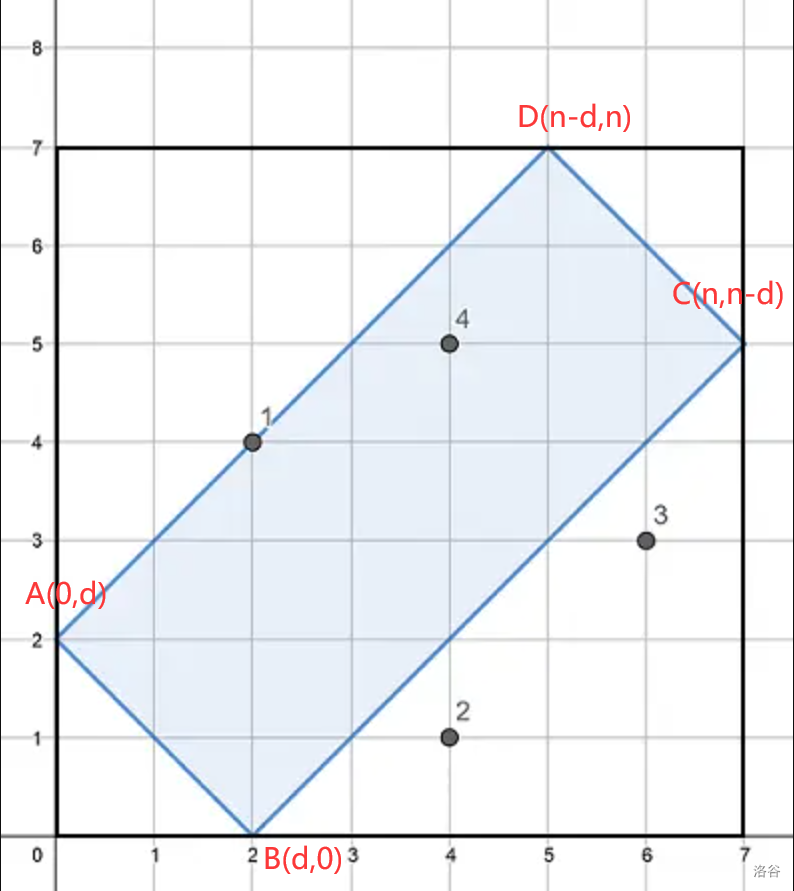
根据公式，斜率 \(k=\dfrac{y_{1}-y_{2}}{x_{1}-x_{2}}\)，截距 \(b=y-kx\) 可得：
\(f(x)=x+d\)；
\(g(x)=-x+2n-d\)；
\(h(x)=x-d\)；
\(i(x)=-x+d\)；
如果一个点 \(P(x_{0},y_{0})\) 要在这个四边形内部，那么 \(x_{0}\in[0,n]\)，\(y_{0}\in[h(x_{0}),f(x_{0})]\cap[i(x_{0}),g(x_{0})]\)。

用不等式表达就是：
\(x_{0}+y_{0}\geqslant d\)；
\(x_{0}+y_{0}\leqslant 2n-d\)；
\(x_{0}-y_{0}\geqslant -d\)；
\(x_{0}-y_{0}\leqslant -d\)。

总之，只要这个点的坐标满足上述四个不等式，那么这个点就在四边形里。

Code

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n,d,x,y,k;
int main(){
	ios::sync_with_stdio(false);
	cin.tie(0),cout.tie(0);//加速cin和cout，可删
	cin>>n>>d>>k;
	for(ll i=0;i<k;++i){
		cin>>x>>y;
		if(x+y>=d && x+y<=2*n-d && x-y>=-d && x-y<=d) cout<<"YES"<<endl;
		else cout<<"NO"<<endl;
    }
	return 0;
}

好水