2025/6/4

分段函数图形绘制

代码
`import numpy as np
import matplotlib.pyplot as plt

定义区间：[-2, 2]，取1000个点使曲线平滑

x = np.linspace(-2, 2, 1000)

计算函数值

注意：函数分为两部分，但根据公式来看，表达式可能是一个整体而非分段函数

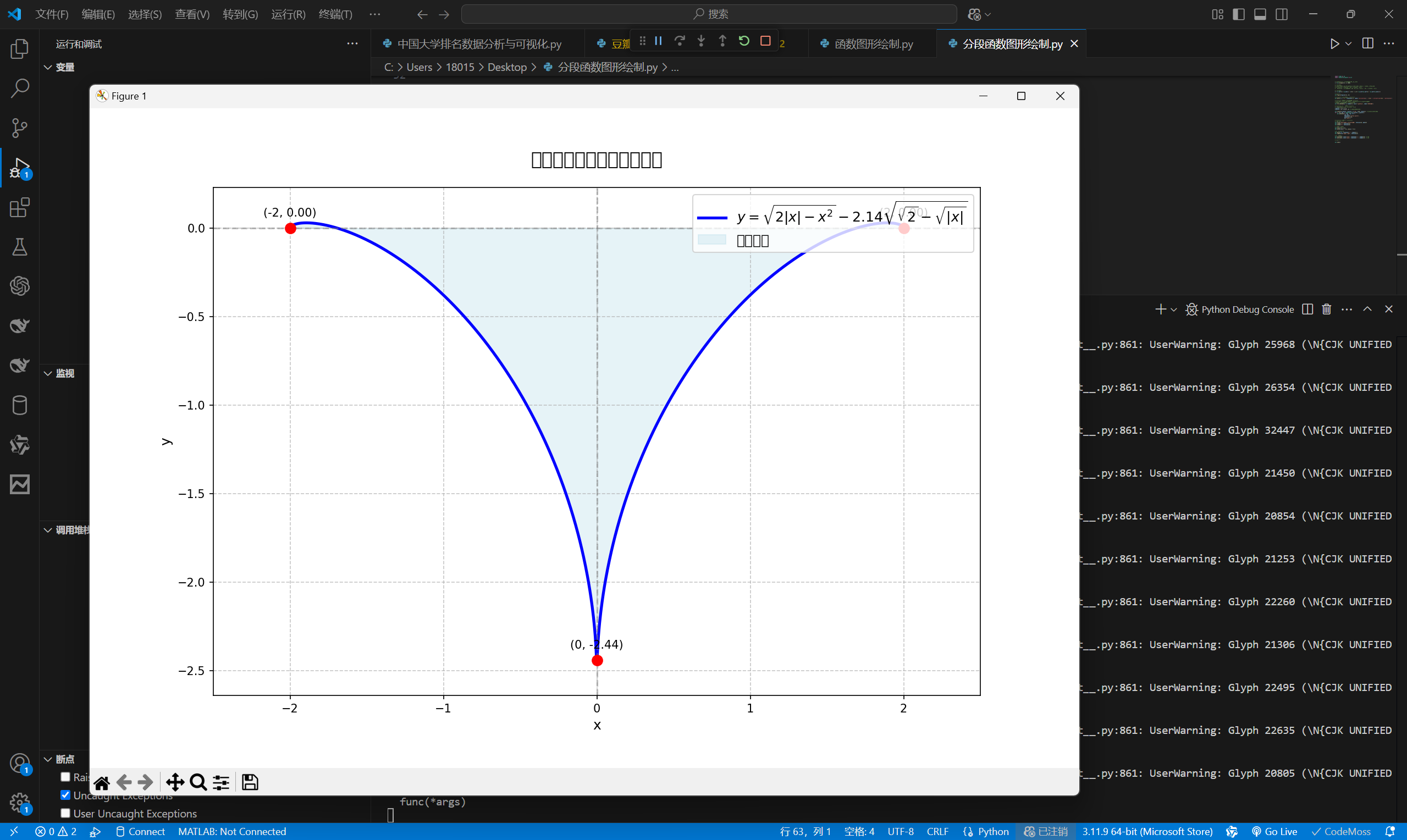
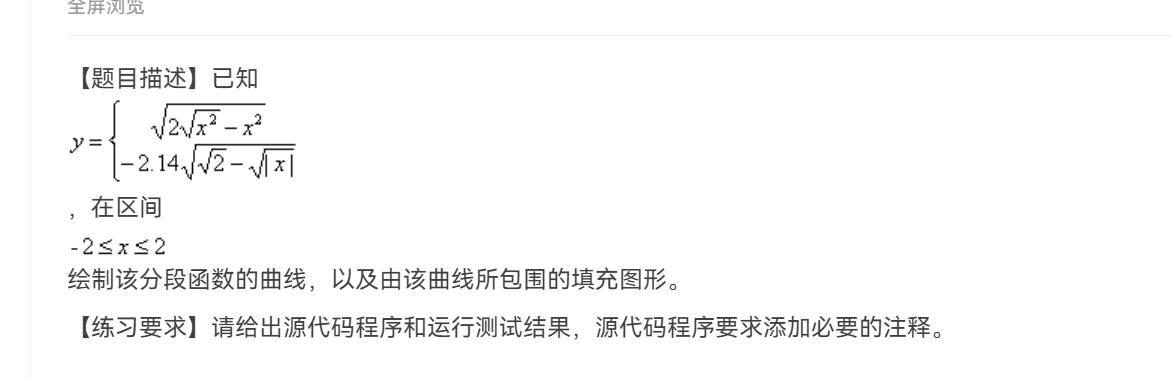
公式解读：y = √(2√(x²) - x²) - 2.14√(√2 - √|x|)

简化：√(x²) = |x|，因此表达式可简化为：y = √(2|x| - x²) - 2.14√(√2 - √|x|)

计算函数值

y = np.sqrt(2 * np.abs(x) - x**2) - 2.14 * np.sqrt(np.sqrt(2) - np.sqrt(np.abs(x)))

创建图形

plt.figure(figsize=(12, 8))

========== 绘制函数曲线 ==========

plt.plot(x, y, 'b-', linewidth=2.5, label=r'$y=\sqrt{2|x| - x^{2}} - 2.14\sqrt{\sqrt{2} - \sqrt{|x|}}$')

========== 填充曲线包围的区域 ==========

根据函数性质，它是偶函数（关于y轴对称），在[-2,2]区间定义域内

填充曲线下方的区域，使用半透明蓝色

plt.fill_between(x, y, alpha=0.3, color='lightblue', label='填充区域')

========== 添加标记点 ==========

标记特殊点：(-2,0), (0,y_min), (2,0)

x_points = [-2, 0, 2]
y_points = [0, y.min(), 0] # 获取x=0时的函数值

plt.scatter(x_points, y_points, c='red', s=80, zorder=5) # zorder确保点在顶层
for i, (xp, yp) in enumerate(zip(x_points, y_points)):
plt.annotate(f'({xp}, {yp:.2f})',
(xp, yp),
textcoords="offset points",
xytext=(0, 10),
ha='center')

========== 美化图形 ==========

设置标题和标签

plt.title('分段函数曲线及其包围区域', fontsize=16, pad=20)
plt.xlabel('x', fontsize=12)
plt.ylabel('y', fontsize=12)

设置坐标轴范围

plt.xlim(-2.5, 2.5)
plt.ylim(y.min() - 0.2, max(y) + 0.2)

添加网格、图例

plt.grid(True, linestyle='--', alpha=0.7)
plt.legend(loc='upper right', fontsize=12)

添加对称虚线

plt.axvline(0, color='gray', linestyle='--', alpha=0.5) # y轴
plt.axhline(0, color='gray', linestyle='--', alpha=0.5) # x轴

显示图形

plt.show()

`
结果