Day12 二叉树part02| LeetCode 226. 翻转二叉树，101. 对称二叉树，104. 二叉树的最大深度，11.二叉树的最小深度

翻转二叉树

• 以每个中间节点为轴，镜像翻转
• 采用前序或后序遍历

226. 翻转二叉树

class Solution {
        public TreeNode invertTree(TreeNode root) {
        if(root==null)return null;
        invertTree(root.left);
        invertTree(root.right);
        swap(root);
        return root;


        }
          void swap(TreeNode root)
        {
            TreeNode tmp=root.left;
            root.left=root.right;
            root.right=tmp;
        }


    }

对称二叉树

101. 对称二叉树

• 通过判断根节点的左右子树是否相互翻转，比较的是子树，不是左右孩子节点

• 通过判断两颗子树的里侧和外侧是否相等

• 后序遍历，一个左右中，一个右左中

• 递归

  1. 确定参数和返回值

  2. 终止 条件

     • 节点存在为空的情况

       • 左节点为空，右节点不为空,false
       • 左不为空，右为空，false
       • 左右都为空，true

     • 不为空的情况

       • 比较左、右节点的值，相同true，否则false

  3. 确定单层循环的逻辑

class Solution {
        public boolean isSymmetric(TreeNode root) {

           return compare(root.left,root.right);

        }
        private  boolean compare(TreeNode left,TreeNode right)
        {
            if(left==null&& right!=null)
            {
                return false;
            }
            if(left!=null&& right==null)
            {
                return false;
            }
            if(left==null&& right==null)
            {
                return true;
            }
            if(left.val!=right.val)
            {
                return false;
            }

//            外侧
            boolean Outside=compare(left.left,right.right);

//            内侧
            boolean Inside=compare(left.right,right.left);

            return Outside&&Inside;
        }

    }

二叉树的最大深度

二叉树节点的深度和高度

• 深度：从根节点到该节点的最长简单路径边的节点数（取决于深度从0开始还是从1开始，力扣从1开始）
• 高度：从该节点到叶子节点的最长简单路径边的节点数（取决于高度从0开始还是从1开始，力扣从1开始）

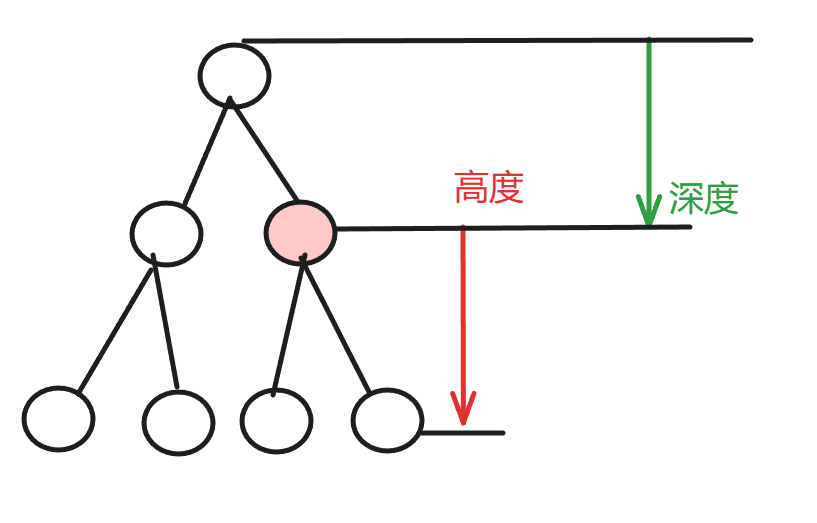
• 根节点的高度就是二叉树的最大深度，因此本题求最大深度就是求高度

104. 二叉树的最大深度

 class Solution {
        public List<List<Integer>> reList=new ArrayList<List<Integer>>();
        public int maxDepth(TreeNode root)  {
            check(root);
            return reList.size();

        }
        public  void check(TreeNode node){

            //判空
            if(node==null)
                return;

            Queue<TreeNode> q=new LinkedList<TreeNode>();
            //根节点 入队
            q.offer(node);
            while(!q.isEmpty())
            {
                List<Integer> itemlist=new ArrayList<Integer>();//存放每层节点
                int lens=q.size();
                while(lens>0)
                {
                    TreeNode tmp=q.poll();//出队
                    itemlist.add(tmp.val);
                    if(tmp.left!=null)
                    {
                        q.offer(tmp.left);
                    }
                    if(tmp.right!=null)
                    {
                        q.offer(tmp.right);
                    }

                    lens--;

                }
                reList.add(itemlist);
            }


        }

    }

二叉树的最小深度

111.二叉树的最小深度

• 最小深度：根节点到最近叶子节点的最短路径上的节点数量

   class Solution {
        public int minDepth(TreeNode root) {

            if(root==null)return 0;

            int leftDepth=minDepth(root.left);
            int rightDepth=minDepth(root.right);

            if(root.left==null)
            {
                return rightDepth+1;
            }
            if(root.right==null)
            {
                return  leftDepth+1;
            }
            return Math.min(leftDepth,rightDepth)+1;



        }
    }