CSP-S-01做题记录

这里有更好的阅读体验

title: CSP-S 01 做题记录
mathjax: true
date: 2025-07-12 06:42:14
tags:

C++
categories:
做题记录
czos

Latest Updated: 2025.07.14

T1 禁卫军

:::details 点击展开题面

A. 禁卫军

题目描述

数字王国正在挑选最强壮，最独一无二的勇士作为国王的禁卫军。

有 \(n\) 个数字士兵参与了这次选拔，分别为 \(w_1, w_2, \dots, w_n\)。其中可能存在多个相同的数字士兵，选拔的条件是：如果这个数不能被剩下的 \(n - 1\) 个数整除，就可以成为禁卫军。

请问，其中会有多少个士兵能顺利加入禁卫军。

输入

第一行读入一个整数 \(n\)。

第二行读入 \(n\) 个整数表示所有数字士兵 \(w_i\)，用空格隔开。

输出

输出一个整数，表示有多少个士兵能顺利加入禁卫军。

样例

样例 1

输入：

5  
3 7 9 16 17

输出：

样例 2
输入：

5  
1 2 3 4 5

输出：

样例 3
输入：

5  
2 2 3 3 5

输出：

说明

样例 1 解释：
数列中 \(3, 7, 16, 17\) 不能被数列中其它整数整除，\(9\) 会被 \(3\) 整除，所以有 \(4\) 个。
数据规模：
- \(1 \le w_i \le 10^6\)。
- 对于 \(50\%\) 的数据：\(1 \le n \le 10000\)。
- 对于 \(100\%\) 的数据：\(1 \le n \le 100000\)。

:::

T1 Sol

问题描述：
求有多少个数，不能被自己以外的其他数字整除。

部分分思路

若暴力枚举，需遍历每个数与其他数的整除关系，时间复杂度为 \(\mathcal{O}(n^2)\) 。

满分思路

样例隐含规律：若存在 1，则其他数会被 1整除；但多个 1间可互相整除。

可借鉴埃筛思想，标记不符合要求的数：

先将数排序，再从小到大遍历。对每个未被标记的数，标记其所有倍数为「不符合要求」（因这些倍数能被当前数整除）。
枚举到某数时，若未被标记为「不符合要求」，则该数可能符合条件。
若存在相等的数，第 \(1\) 个虽可能未被标记，但相等数间可互相整除，一定不符合要求 。

:::warning 注意！
对于相同的数，他们可以互相牵制，都不算做合法答案。

:::

T1 Code

/*
 * > CPP Code Snippet <
 * > Powered by Microsoft Visual Studio Code <
 *
 * @Author    FrankWKD (wangkedi01)
 * @Date      2025-07-09
 * @Network   "https://oj.czos.cn/contest/problem?id=25410&pid=0"
 * @License   GNU General Public License 2.0
 * @Platform  [Frank]iMac Ubuntu Pro 24.04 LTS
 * @FileName  T1.cpp
 * @FilePath  /media/frank/FrankW/_default/_Mine!/Working/code-spaces/czos/CSP-S_Practise/Lesson1/T1.cpp
 * @Solution  --
 */

// #pragma GCC optimize(3)
#include <bits/stdc++.h>
using namespace std;
int a[1010100];
int n;
bool f[1010100];
int ans;
int main() {
    // freopen("sample.in","r",stdin);
    // freopen("sample.out","w",stdout);
    // ios::sync_with_stdio(false);
    // cin.tie(0); cout.tie(0);
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }
    sort(a + 1, a + 1 + n);
    if (a[1] == 1) {
        if (a[2] != 1)
            cout << 1;
        else
            cout << 0;
        return 0;
    }
    for (int i = 1; i <= n; i++) {
        if (!f[a[i]] and a[i] != a[i + 1])  // 如果相邻的相等还不行呢
            ans++;
        for (int j = a[i]; j <= a[n]; j += a[i]) {
            f[j] = 1;
        }
    }
    cout << ans << endl;
    // fclose(stdin);
    // fclose(stdout);
    return 0;
}

T2 [CSP-S2024]决斗

:::details 点击展开题面

P11231 [CSP-S 2024] 决斗

题目描述

今天是小 Q 的生日，他得到了 \(n\) 张卡牌作为礼物。这些卡牌属于火爆的“决斗怪兽”，其中，第 \(i\) 张卡代表一只攻击力为 \(r_i\)，防御力也为 \(r_i\) 的怪兽。

一场游戏分为若干回合。每回合，小 Q 会选择某只怪兽 \(i\) 以及另一只怪兽 \(j(i \neq j)\)，并让怪兽 \(i\) 向怪兽 \(j\) 发起攻击。此时，若怪兽 \(i\) 的攻击力小于等于怪兽 \(j\) 的防御力，则无事发生；否则，怪兽 \(j\) 的防御被打破，怪兽 \(j\) 退出游戏不再参与到剩下的游戏中。一只怪兽在整场游戏中至多只能发起一次攻击。当未退出游戏的怪兽都已发起过攻击时，游戏结束。

小 Q 希望决定一组攻击顺序，使得在游戏结束时，未退出游戏的怪兽数量尽可能少。

输入格式

输入的第一行包含一个正整数 \(n\)，表示卡牌的个数。

输入的第二行包含 \(n\) 个正整数，其中第 \(i\) 个正整数表示第 \(i\) 个怪兽的攻击力及防御力 \(r_i\)。

输出格式

输出一行包含一个整数表示游戏结束时未退出游戏的怪兽数量的最小值。

输入输出样例 #1

输入 #1

5
1 2 3 1 2

输出 #1

输入输出样例 #2

输入 #2

10
136 136 136 2417 136 136 2417 136 136 136

输出 #2

说明/提示

【样例 1 解释】

其中一种最优方案为：第一回合让第 \(2\) 只怪兽向第 \(1\) 只怪兽发起攻击，第二回合让第 \(5\) 只怪兽向第 \(4\) 只怪兽发起攻击，第三回合让第 \(3\) 只怪兽向第 \(5\) 只怪兽发起攻击。此时没有退出游戏的怪兽都进行过攻击，游戏结束。可以证明没有更优的攻击顺序。

【样例 3】

见选手目录下的 duel/duel3.in 与 duel/duel3.ans。

该样例满足 \(\forall 1 \leq i \leq n, r_i \leq 2\)。

【样例 4】

见选手目录下的 duel/duel4.in 与 duel/duel4.ans。

【数据范围】

对于所有测试数据，保证：\(1 \leq n \leq 10^5\)，\(1 \leq r_i \leq 10^5\)。

测试点	\(n\)	\(r_i\)	特殊性质
\(1\sim 4\)	\(\leq 10\)	\(\leq 10^5\)	无特殊性质
\(5\sim 10\)	\(\leq 10^5\)	\(\leq 2\)	无特殊性质
\(11\sim 15\)	\(\leq 30\)	\(\leq 10^5\)	特殊性质 A
\(16\sim 20\)	\(\leq 10^5\)	\(\leq 10^5\)	无特殊性质

特殊性质 A：保证每个 \(r_i\) 在可能的值域中独立均匀随机生成。

:::

T2 Sol

采用贪心策略，结合双指针配对：
假设存在三个数满足 \(a < b < c\)，若 \(c\) 选择击败 \(a\)，则 \(b\) 无可以击败的对象（因 \(b\) 仅能击败比它小的数，而比 \(b\) 小的 \(a\) 已被 \(c\) 击败）。
基于此规律，可用双指针法对数组排序后进行配对，优化剩余数的计算逻辑，得到最少剩余数量。

（注：完整实现需先对数组排序，再通过指针模拟攻击配对过程，此处为核心思路提炼。）

T2 Code

/*
 * > CPP Code Snippet <
 * > Powered by Microsoft Visual Studio Code <
 *
 * @Author    FrankWKD (wangkedi01)
 * @Date      2025-07-09
 * @Network   "https://oj.czos.cn/contest/problem?id=25410&pid=1"
 * @License   GNU General Public License 2.0
 * @Platform  [Frank]iMac Ubuntu Pro 24.04 LTS
 * @FileName  T2.cpp
 * @FilePath  /media/frank/FrankW/_default/_Mine!/Working/code-spaces/czos/CSP-S_Practise/Lesson1/T2.cpp
 * @Solution  -
 */

// #pragma GCC optimize(3)
#include <bits/stdc++.h>
using namespace std;
const int N = 100005;
int a[N], n;
bool cmp(int m, int b) {
    return m > b;
}
int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) {
        scanf("%d", &a[i]);
    }
    sort(a + 1, a + n + 1, cmp);
    int ans = n;
    for (int i = n, j = n; i >= 1; i--) {
        if (a[i] > a[j]) {
            j--;
            ans--;
        }
    }
    printf("%d", ans);
    return 0;
}

T3 [CSP-S 2024] 超速检测

:::details 点击展开题面

P11232 [CSP-S 2024] 超速检测

题目描述

小 D 新入职了某国的交管部门，他的第一个任务是负责国家的一条长度为 \(L\) 的南北主干道的车辆超速检测。为了考考小 D，上司首先需要他解决一个简化的场景。

这个周末，主干道上预计出现 \(n\) 辆车，其中第 \(i\) 辆车从主干道上距离最南端 \(d_i\) 的位置驶入，以 \(v_i\) 的初速度和 \(a_i\) 的加速度做匀加速运动向北行驶。我们只考虑从南向北的车辆，故 \(v_i > 0\)，但 \(a_i\) 可正可负，也可以为零。当车辆行驶到主干道最北端（即距离最南端为 \(L\) 的位置）或速度降为 \(0\)（这只可能在 \(a_i < 0\) 时发生）时，我们认为该车驶离主干道。

主干道上设置了 \(m\) 个测速仪，其中第 \(j\) 个测速仪位于主干道上距离最南端 \(p_j\) 的位置，每个测速仪可以设置开启或关闭。当某辆车经过某个开启的测速仪时，若这辆车的瞬时速度超过了道路限速 \(V\)，那么这辆车就会被判定为超速。注意当车辆驶入与驶出主干道时，如果在对应位置有一个开启的测速仪，这个测速仪也会对这辆车进行测速。

上司首先想知道，如果所有测速仪都是开启的，那么这 \(n\) 辆车中会有多少辆车被判定为超速。

其次，为了节能，部门想关闭一部分测速仪。然而，他们不希望漏掉超速的车，也就是说，当 \(n\) 辆车里的某辆车在所有测速仪都开启时被判定为超速，他们希望在关闭一部分测速仪以后它依然被判定为超速。上司还想知道在这样的条件下最多可以关闭多少测速仪。

由于 \(n\) 很大，上司允许小 D 使用编程解决这两个问题，于是小 D 找到了你。

如果你对于加速度并不熟悉，小 D 贴心地在本题的“提示”部分提供了有关加速度的公式。

输入格式

输入的第一行包含一个正整数 \(T\)，表示数据组数。

接下来包含 \(T\) 组数据，每组数据的格式如下：

第一行包含四个整数 \(n, m, L, V\)，分别表示车辆数量、测速仪数量、主干道长度和道路限速。

接下来 \(n\) 行：

第 \(i\) 行包含三个整数 \(d_i, v_i, a_i\) 描述一辆车。

最后一行包含 \(m\) 个整数 \(p_1, p_2, \dots , p_m\) 描述道路上所有测速仪的位置。

输出格式

对于每组数据：输出一行包含两个整数，第一个整数为所有测速仪都开启时被判定为超速的车辆数量，第二个整数为在不漏掉超速车辆的前提下最多可以关闭的测速仪数量。

输入输出样例 #1

输入 #1

输出 #1

3 3

说明/提示

【样例 1 解释】

在该组测试数据中，主干道长度为 \(15\)，限速为 \(3\)，在距离最南端 \(2, 5, 8, 9, 15\) 的位置各设有一个测速仪。

第一辆车在最南端驶入，以 \(3\) 的速度匀速行驶。这辆车在整个路段上都没有超速。
第二辆车在距离最南端 \(12\) 的位置驶入，以 \(4\) 的速度匀速行驶。在最北端驶离主干道时，它会被距离最南端 \(15\) 的测速仪判定为超速。
第三辆车在距离最南端 \(1\) 的位置驶入，以 \(1\) 的初速度、\(4\) 的加速度行驶。其在行驶了 \(\frac{3^2-1^2}{2\times 4}=1\) 的距离，即到达 \(2\) 的位置时，速度变为 \(3\)，并在之后一直超速。因此这辆车会被除了距离最南端 \(2\) 的测速仪以外的其他测速仪判定为超速。
第四辆车在距离最南端 \(5\) 的位置驶入，以 \(5\) 的初速度、\(-2\) 的加速度行驶。其在行驶了 \(\frac{3^2-5^2}{2\times (-2)}\) 的距离，即到达 \(9\) 的位置时，速度变为 \(3\)。因此这辆车在距离最南端 \([5, 9)\) 时超速，会被距离最南端 \(5\) 和 \(8\) 的两个测速仪判定为超速。
第五辆车在距离最南端 \(6\) 的位置驶入，以 \(4\) 的初速度、\(−4\) 的加速度行驶。在其行驶了 \(\frac{3^2-4^2}{2\times (-4)}=\frac{7}{8}\) 的距离后，即这辆车到达 \(6\frac{7}{8}\) 的位置时，其速度变为 \(3\)。因此这辆车在距离最南端 \([6,6\frac{7}{8})\) 时超速，但这段区间内没有测速仪，因此不会被判定为超速。

因此第二、三、四辆车会被判定为超速，输出的第一个数为 \(3\)。

我们可以关闭距离最南端 \(2, 8, 9\) 的三个测速仪，保留 \(5\) 和 \(15\) 的两个测速仪，此时三辆之前被判定为超速的车依然被判定为超速。可以证明不存在更优方案，因此输出的第二个数为 \(3\)。

【样例 2】

见选手目录下的 detect/detect2.in 与 detect/detect2.ans。

该组样例满足 \(n, m \leq 10\)。

【样例 3】

见选手目录下的 detect/detect3.in 与 detect/detect3.ans。

该组样例满足特殊性质 A，其中前十组测试数据满足 \(n, m \leq 3000\)。

【样例 4】

见选手目录下的 detect/detect4.in 与 detect/detect4.ans。

该组样例满足特殊性质 B，其中前十组测试数据满足 \(n, m \leq 3000\)。

【样例 5】

见选手目录下的 detect/detect5.in 与 detect/detect5.ans。

该组样例满足特殊性质 C，其中前十组测试数据满足 \(n, m \leq 3000\)。

【数据范围】

对于所有测试数据，保证：

\(1 \leq T \leq 20\)；
\(1 \leq n, m \leq 10^5\)，\(1 \leq L \leq 10^6\)，\(1 \leq V \leq 10^3\)；
\(0 \leq d_i < L\)，\(1 \leq v_i \leq 10^3\)，\(|a_i| \leq 10^3\)；
\(0 \leq p_1 < p_2 < \dots < p_m \leq L\)。

测试点	\(n,m\leq\)	特殊性质
\(1\)	\(10\)	无
\(2\)	\(20\)	无
\(3\)	\(3000\)	A
\(4\)	\(10^5\)	A
\(5\)	\(3000\)	B
\(6\)	\(10^5\)	B
\(7\)	\(3000\)	C
\(8\)	\(10^5\)	C
\(9\)	\(3000\)	无
\(10\)	\(10^5\)	无

特殊性质 A：保证 \(a_i = 0\)。

特殊性质 B：保证 \(a_i > 0\)。

特殊性质 C：保证 \(a_i < 0\)，且所有车都不在最北端驶离主干道。

【提示】

与加速度有关的定义和公式如下：

匀加速运动是指物体在运动过程中，加速度保持不变的运动，即每单位时间内速度的变化量是恒定的。
当一辆车的初速度为 \(v_0\)、加速度 \(a\neq 0\)，做匀加速运动，则 \(t\) 时刻后它的速度 \(v_1 = v_0 + a \times t\)，它的位移（即行驶路程）\(s=v_0\times t+0.5\times a\times t^2\)。
当一辆车的初速度为 \(v_0\)、加速度 \(a \neq 0\)，做匀加速运动，则当它的位移（即行驶路程）为 \(s\) 时，这辆车的瞬时速度为 \(\sqrt{v_0^2+2\times a\times s}\)。
当一辆车的初速度为 \(v_0\)、加速度 \(a \neq 0\)，在它的位移（即行驶路程）为 \(\frac{v_1^2-v_0^2}{2a}\) 时，这辆车的瞬时速度为 \(v_1\)。

如果你使用浮点数进行计算，需要注意潜在的精度问题。

:::

T3 Sol

C - 超速检测 [CSP-S 2024]

题意：

道路长度 \(L\)，有 \(n\) 辆车，第 \(i\) 辆车出现在 \(d_i\) 点，以 \(v_i\) 的初速度和 \(a_i\) 的加速度运动。
\(a_i\) 可正负或 \(0\)，当车辆到达 \(L\) 或者速度为 \(0\)（\(a_i \lt 0\)），表示离开道路。
有 \(m\) 个测速仪，第 \(j\) 个测速仪在 \(p_j\) 位置，如果车到达 \(p_j\) 位置车速 \(\gt v\)，则超速。

求：

如果测速仪都开启，有几辆被监控拍到超速。
可以最多关闭几个测速仪，保证还是能测到所有测速仪都打开时的超速车。

以下是为内容中的字母、数字等加上 LaTeX 格式（主要是对变量、公式等进行数学环境标记）后的排版，内容本身未做修改：

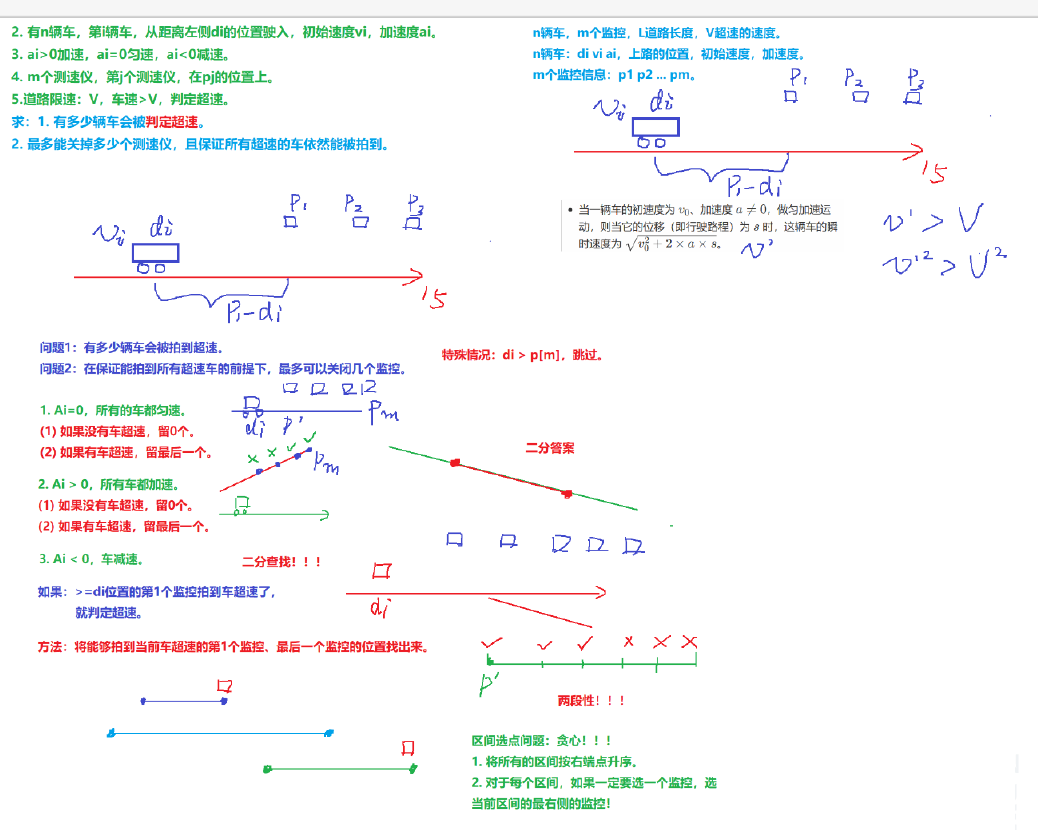
思路：

1. 特判特殊性质 \(A\) 匀速行驶。

对于匀速行驶的情况，只有一开始超速，才会被认定为超速。
关闭几个测速仪：没有车被拍到超速，关 \(m\) 个，有车被拍到超速，关 \(m\text{-}1\) 个，留最后一个。

2. \(100\) 分的讨论。

1. 关于超速情况的讨论。
- 情况一：如果位置 \(d_i > p[m]\)，即\(>\)最后一个监控的位置，拍不到。
- 情况二：如果初始速度 \(v_i \leq v\)，且 \(a_i \leq 0\)，即一开始没有超速，且是匀速或减速，则一定不超速。
- 情况三：如果加速运动，且到最后一个监控的位置，速度还未达到 \(v\)，则不超速。
  - 如何判断从起点 \(d_i\) 到某个位置 \(d_2\) 是否超速？用题目给的公式。
  - 如果满足：\(v_i^2 + 2 * a_i * (d_2 - d_i) > v^2\)，则超速。
- 情况四：如果减速运动，且到 \(d_i\) 后面的第 \(1\) 个监控的位置，速度还未达到 \(v\)，则不超速。
  - \(d_i\) 后面的第 \(1\) 个监控的位置，即：\(p\) 数组中从 \(d_i\) 开始找第 \(1\) 个满足 \(\geq d_i\) 的位置，显然二分。
    其余情况，必然超速。
  - 对于加速运动：二分找到第 \(1\) 个超速的监控位置 \(L\)，从 \(L\) 到 \(m\) 的所有监控都能拍到超速。
    对于减速运动：二分找到最后一个超速的监控位置 \(R\)，从 \(d_i\) 后面的第 \(1\) 个监控到 \(R\) 都能拍到超速。
    将能拍到每辆车超速监控的起止位置存下来，转换为区间选点问题。
1. 关于区间选点问题的讨论
- 按右端点升序，优先讨论可能被“包含”的区间，选点时，优先选择最右侧的点即可。
- 1. 匀速
  - (1) 第 i 辆车是否超速：\(vi > V\)。
  - (2) 最多可以关闭几个测速仪：如果没有车超速，关 \(m\) 个，如果有车超速，打开最后一个，关 \(m-1\) 个。
- 1. 加速
  - (1) 第 i 辆车是否超速：求车到最后一个监控的位置是否超速。
  - (2) 最多可以关闭几个测速仪：如果没有车超速，关 \(m\) 个，如果有车超速，关 \(m-1\) 个。
- 1. 减速
  - (1) 第 i 辆车是否超速：求出 \(\geq di\) 的第 \(1\) 个监控的位置 \(p\)，求到 \(p\) 为止是否超速。
  - (2) 最多可以关闭几个测速仪：计算出能测到当前测速的第 \(1\) 个和最后一个测速仪。将问题转换为区间选点问题。

:::details 点击查看图片附件

cnblogs@FrankWkd
:::

T3 Code [40pts WA]

根据特殊性质骗分。

/*
 * > CPP Code Snippet <
 * > Powered by Microsoft Visual Studio Code <
 *
 * @Author    FrankWKD (wangkedi01)
 * @Date      2025-07-14
 * @Network   "https://oj.czos.cn/contest/problem?id=25410&pid=2"
 * @License   GNU General Public License 2.0
 * @Platform  [Frank]iMac Ubuntu Pro 24.04 LTS
 * @FileName  T3[40pts].cpp
 * @FilePath  /media/frank/FrankW/_default/_Mine!/Working/code-spaces/czos/CSP-S_Practise/Lesson1/T3[40pts].cpp
 * @Solution  --
 */

// #pragma GCC optimize(3)
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
struct node {
    int d, v, a;
} a[N];
int p[N];
int n, m, len, v;
int cnt, res, T;
int pf(int x) {
    return x * x;
}
bool check(int di, int vi, int ai, int ed) {
    return pf(vi) + 2 * ai * (ed - di) > pf(v);
}
int main() {
    // freopen("sample.in","r",stdin);
    // freopen("sample.out","w",stdout);
    // ios::sync_with_stdio(false);
    // cin.tie(0); cout.tie(0);
    cin >> T;
    while (T--) {
        cin >> n >> m >> len >> v;
        for (int i = 1; i <= n; i++) {
            scanf("%d%d%d", &a[i].d, &a[i].v, &a[i].a);
        }
        for (int i = 1; i <= m; i++) {
            cin >> p[i];
        }
        cnt = 0;
        int c0 = 0, c1 = 0;
        for (int i = 1; i <= n; i++) {
            if (a[i].a == 0)
                c0++;
            else if (a[i].a > 0)
                c1++;
            if (a[i].d > p[m])
                continue;
            if (a[i].v > v and a[i].a == 0) {
                cnt++;
                continue;
            }
            if (a[i].a > 0 and check(a[i].d, a[i].v, a[i].a, p[m])) {
                cnt++;
                continue;
            }
        }
        if (c0 == n or c1 == n) {
            if (cnt == 0)
                res = m;
            else
                res = m - 1;
        }
        cout << cnt << " " << res << endl;
    }
    // fclose(stdin);
    // fclose(stdout);
    return 0;
}

T3 Code [100pts AC]

/*
 * > CPP Code Snippet <
 * > Powered by Microsoft Visual Studio Code <
 *
 * @Author    FrankWKD (wangkedi01)
 * @Date      2025-07-14
 * @Network   "https://oj.czos.cn/contest/problem?id=25410&pid=2&_pjax=%23p0"
 * @License   GNU General Public License 2.0
 * @Platform  [Frank]iMac Ubuntu Pro 24.04 LTS
 * @FileName  T3[100pts].cpp
 * @FilePath  /media/frank/FrankW/_default/_Mine!/Working/code-spaces/czos/CSP-S_Practise/Lesson1/T3[100pts].cpp
 * @Solution  --
 */

// #pragma GCC optimize(3)
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
struct node {
    int d, v, a;
} a[N];

struct range {
    int b, e;
} b[N];
int p[N];
int n, m, len, v;
int cnt, T, res;

int pf(int x) {
    return x * x;
}
bool check(int di, int vi, int ai, int ed) {
    return pf(vi) + 2 * ai * (ed - di) > pf(v);
}
pair<int, int> find(int di, int vi, int ai) {
    int t = lower_bound(p + 1, p + m + 1, di) - p;
    if (ai > 0) {
        int l = t;
        int r = m;
        while (l <= r) {
            int mid = l + r >> 1;
            if (check(di, vi, ai, p[mid]))
                r = mid - 1;
            else
                l = mid + 1;
        }
        return {l, m};
    }
    if (ai < 0) {
        int l = t, r = m, mid;
        while (l <= r) {
            mid = l + r >> 1;
            if (check(di, vi, ai, p[mid]))
                l = mid + 1;
            else
                r = mid - 1;
        }
        return {t, l - 1};
    }
}
bool cmp(range r1, range r2) {
    return r1.e < r2.e;
}
int solve() {
    sort(b + 1, b + cnt + 1, cmp);
    int res = 0, ls = -1;
    for (int i = 1; i <= cnt; i++) {
        if (b[i].b > ls) {
            res++;
            ls = b[i].e;
        }
    }
    return m - res;
}

int main() {
    // freopen("sample.in","r",stdin);
    // freopen("sample.out","w",stdout);
    // ios::sync_with_stdio(false);
    // cin.tie(0); cout.tie(0);
    cin >> T;
    while (T--) {
        cin >> n >> m >> len >> v;
        for (int i = 1; i <= n; i++) {
            cin >> a[i].d >> a[i].v >> a[i].a;
        }
        for (int i = 1; i <= m; i++) {
            cin >> p[i];
        }

        cnt = 0;
        int c0 = 0, c1 = 0;
        for (int i = 1; i <= n; i++) {
            if (a[i].a == 0)
                c0++;
            else if (a[i].a > 0)
                c1++;
            if (a[i].d > p[m])
                continue;
            if (a[i].v > v and a[i].a == 0) {
                int st = lower_bound(p + 1, p + m + 1, a[i].d) - p;
                b[++cnt] = {st, m};
                continue;
            }
            if (a[i].v <= v and a[i].a <= 0)
                continue;
            if (a[i].a > 0 and !check(a[i].d, a[i].v, a[i].a, p[m]))
                continue;
            int t = lower_bound(p + 1, p + 1 + m, a[i].d) - p;
            if (a[i].a < 0 and !check(a[i].d, a[i].v, a[i].a, p[t]))
                continue;
            pair<int, int> pos = find(a[i].d, a[i].v, a[i].a);
            cnt++;
            b[cnt] = {pos.first, pos.second};
        }
        if (c0 == n or c1 == n) {
            if (cnt == 0)
                res = m;
            else
                res = m - 1;
        } else
            res = solve();
        cout << cnt << " " << res << endl;
    }
    // fclose(stdin);
    // fclose(stdout);
    return 0;
}

posted @ 2025-07-14 17:31 FrankWkd 阅读(88) 评论(0) 收藏举报

刷新页面返回顶部

Loading

FrankWKD

CSP-S-01做题记录

这里有更好的阅读体验

Latest Updated: 2025.07.14

T1 禁卫军

A. 禁卫军

题目描述

输入

输出

样例

说明

T1 Sol

部分分思路

满分思路

T1 Code

T2 [CSP-S2024]决斗

P11231 [CSP-S 2024] 决斗

题目描述

输入格式

输出格式

输入输出样例 #1

输入 #1

输出 #1

输入输出样例 #2

输入 #2

输出 #2

说明/提示

T2 Sol

T2 Code

T3 [CSP-S 2024] 超速检测

P11232 [CSP-S 2024] 超速检测

题目描述

输入格式

输出格式

输入输出样例 #1

输入 #1

输出 #1

说明/提示

T3 Sol

C - 超速检测 [CSP-S 2024]

题意：

求：

思路：

1. 特判特殊性质 \(A\) 匀速行驶。

2. \(100\) 分的讨论。

T3 Code [40pts WA]

T3 Code [100pts AC]