【专题】最易懂的最短路算法

【专题】图论：最短路算法

Updated At 2025.02.28 22:01

本文遵守GNU GPL2.0开源协议。

---

---

前置知识

单源最短路：

• 指使用一次算法能够求出某个指定点到其他的最短距离。
• 说人话：求跑一次算法只能求出一个点到其他所有点的最短路。

多源最短路：

• 跑一遍算法之后任意两个顶点的最短路都可以得到。

---

---

\(Dijkatra\) 单源最短路

• 要求：边权全部非负
• 核心： 每次用距离较短的点更新其他点的距离
• 复杂度： \(O(n^2)\)
• 为什么要更新某个点的距离呢？
  • 很简单，因为可能某些看似较为简单的路径并不是最优解。详见下图：
  • 
  • 很明显，从 \(1\) 走到 \(3\) 的捷径显然没有 \(1->2->3\) 的路径长度小。

过程

• 我们来模拟一下这个过程。
• 如图，设 \(dis_i\) 存储当前起始点到 \(i\) 点的当前最短路径长度，\(check_i\) 则表示是否确定 \(dis_i\) 的值为起始点到 \(i\) 点的最优路径长度，如果打钩✅，就代表 \(dis_i\) 中的值已经是最短路径了，反之则代表这个值还会被更新。
• 目标：计算从 \(1\) 点到 \(6\) 点的最短路径长度。
  
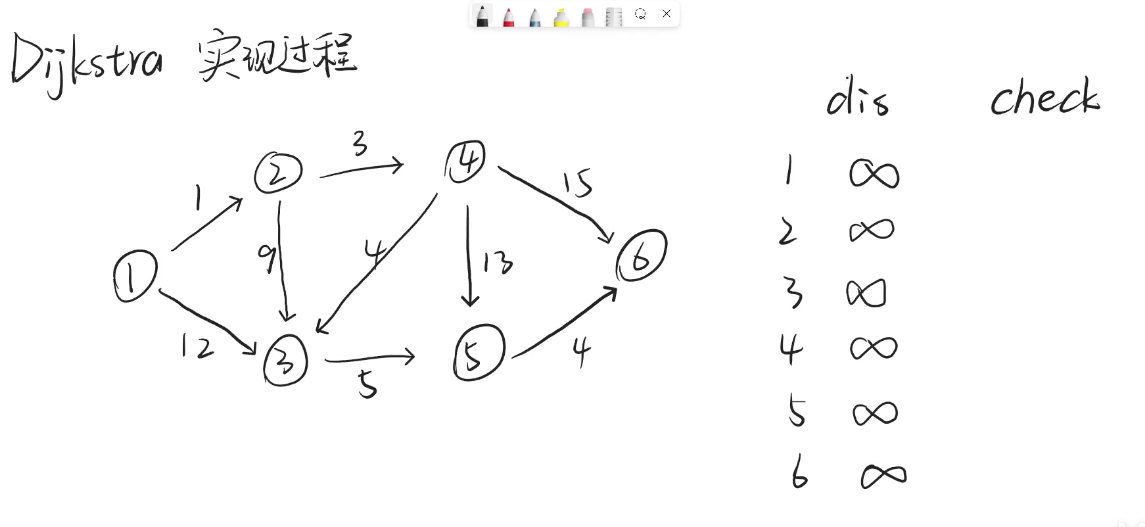
• \(1\) 点到 \(1\) 点的距离是 \(0\) ，因为不需要移动。
• 因为 \(0\) 比 \(\infty\) 小，所以我们更新 \(dis_1\) 的值为 \(1\).
  
• 接下来我们找所有 \(dis\) 里面的最小值，然后标记 \(check\) 中的那个点为 \(true\) (后期可以使用堆).
• 然后我们遍历所有点来寻找最短路。详见：Link