数据结构与算法（1）数据组织方式、空间利用率、算法的重要性——ZJU

数据结构与算法（1）数据组织方式、空间利用率、算法的重要性——ZJU

1.1数据结构基本概念

1.1.1解决问题方法的效率， 跟数据的组织方式有关

思考问题：如何在书架上摆放图书？

不同的摆放方法（即数据的组织方式），影响着插入新图书与查找图书的效率（即解决问题方法的效率），例如，乱放与按类归类后按字母顺序排列。

故有：解决问题方法的效率， 跟数据的组织方式有关

---

1.1.2解决问题方法的效率， 跟空间的利用效率有关

循环法与递归法实现例子

例2：写程序实现一个函数PrintN，使得
传入一个正整数为N的参数后，能顺序
打印从1到N的全部正整数

循环法：

void PrintN ( int N )
{ int i;
for ( i=1; i<=N; i++ ){
printf(“%d\n”, i );
}
return;
}

递归法：

void PrintN ( int N )
{ if ( N ){//N!=0时进行递归调用，N==0时直接返回，故打印时从1开始
PrintN( N – 1 ); 
printf(“%d\n”, N );
}
return;
} 

运行后会发现递归法并不能满足要求，直接跳出（吃内存），循环法正常运行。

故有：解决问题方法的效率， 跟空间的利用效率有关

---

1.1.3解决问题方法的效率， 跟算法的巧妙程度有关

幂指数多项式求和——循环累次相加和秦九韶算法

写程序计算给定多项式在给定点x
处的值

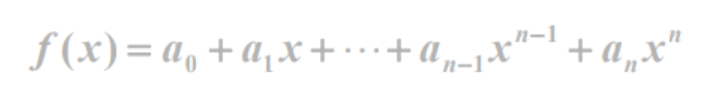
//循环累次相加:

double f( int n, double a[], double x )
{ int i;
double p = a[0];
for ( i=1; i<=n; i++ )
p += (a[i] * pow(x, i)); 
return p;
} 

//秦九韶算法:

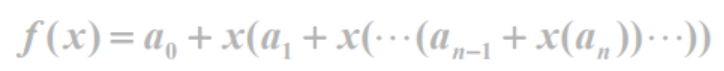
double f( int n, double a[], double x )
{ int i;
double p = a[n];
for ( i=n; i>0; i-- )
p = a[i-1] + x*p;
return p;
} 

两者的运行时间是不相同的，进行运行测试：

其中注意几点：

1. 使用clock()进行时钟计时

   clock()：捕捉从程序开始运行到clock()被调用时所耗费的时间。这个
   时间单位是clock tick，即“时钟打点”。
   //其中常数CLK_TCK(或CLOCKS_PER_SEC)：机器时钟每秒所走的时钟打点数
   

2. 当运行程序的时间太短但必须要进行计时时，可以重复运行N次（循环），测算时间后/N。

普通的运行一次计时程序：

#include <stdio.h>
#include <time.h>
clock_t start, stop;/* clock_t是clock()函数返回的变量类型 */
double duration;/* 记录被测函数运行时间，以秒为单位 */
int main ()
{ /* 不在测试范围内的准备工作写在clock()调用之前*/
start = clock(); /* 开始计时 */
MyFunction(); /* 把被测函数加在这里 */
stop = clock(); /* 停止计时 */
duration = ((double)(stop - start))/CLK_TCK;
    /* 计算运行时间 */
    /* 其他不在测试范围的处理写在后面，例如输出duration的值 */
return 0;
} 

添加了重复运行后的实现程序：

#include <stdio.h>
#include <time.h>
#include <math.h>
define MAXK 1e7 /* 被测函数最大重复调用次数 */
clock_t start, stop; 
double duration;
#define MAXN 10 /* 多项式最大项数，即多项式阶数+1 */
double f1( int n, double a[], double x );
double f2( int n, double a[], double x );
int main ()
{ int i;
double a[MAXN]; /* 存储多项式的系数 */
for ( i=0; i<MAXN; i++ ) a[i] = (double)i; 
start = clock();
for ( i=0; i<MAXK; i++ ) /* 重复调用函数以获得充分多的时钟打点数*/
	f1(MAXN-1, a, 1.1);
stop = clock();
duration = ((double)(stop - start))/CLK_TCK/MAXK; 
printf("ticks1 = %f\n", (double)(stop - start));
printf("duration1 = %6.2e\n", duration);
start = clock();
for ( i=0; i<MAXK; i++ ) /* 重复调用函数以获得充分多的时钟打点数*/
	f2(MAXN-1, a, 1.1); 
stop = clock();
duration = ((double)(stop - start))/CLK_TCK/MAXK; 
printf("ticks2 = %f\n", (double)(stop - start));
printf("duration2 = %6.2e\n", duration);
return 0
}

故有：解决问题方法的效率， 跟算法的巧妙程度有关

---

1.1.4抽象数据类型（Abstract Data Type ）

• 数据类型

  ​ 数据对象集

  ​ 数据集合相关联的操作集

  （可能面向对象的编程语言更容易理解。）

• 抽象：描述数据类型的方法不依赖于具体实现

​ 与存放数据的机器无关

​ 与数据存储的物理结构无关

​ 与实现操作的算法和编程语言均无关

只描述数据对象集和相关操作集 “是什么 ”，并不涉及 “如何做到 ”的问题

---

个人的理解：

• 抽象数据类型类似于“概念”一说，并不涉及具体、个别，而是使用抽象的概括进行说明，可以认为即为大纲，不过分细分内容，不涉及如何具体实现，该抽象数据类型可以适用于个别具体的对象（对象集和操作集）。
• 数据结构的含义，大体为数据对象中数据的联系及对数据的操作、函数。
• 该节课讲的内容为：数据组织方式、空间利用率、算法的重要性。