稍微记一些 dp 优化方法

每个借一题讲解一下方法，剩下做的有可能比较无聊就没记，不无聊的在其他地方记吧。

P3648 [APIO2014] 序列分割

斜率优化经典题目。首先先把朴素 dp 列出来，其实也不简单，因为最先看出来的是区间 dp。但是我们要证明切割的顺序对答案是没有影响的，我们使用调整归纳证明。

\(Proof.\) 选取三段 \(a,b,c\)。我们第一次先切开 \(a\) 和 \(b\) 之间，第二次先切开 \(b\) 和 \(c\) 之间。

第一次的总答案为：\(a\times (b+c)+b\times c=a\times b+b\times c+c\times a\)

第二次的总答案为：\(c\times (a+b)+a\times b=a\times b+b\times c+c\times a\)

注意到这两个显然是相等的，于是可以归纳证毕。

那么我们把 dp 变为了线性 dp。设 \(f_{i,k}\) 为考虑切割前 \(i\) 个，一共切了 \(k\) 刀的最大价值。转移时，我们可以使用强制的思想（这已经非常常见了），假设砍在了 \(j\)，那么把这一刀提前到当前的第一刀，则贡献为 \(Sum_j\times (Sum_i-Sum_j)\)，则转移呼之欲出，\(f_{i,k}=\max\{f_{j,k-1}+Sum_j\times (Sum_i-Sum_j)\}\)，这很显然是一个斜率优化的形式，我们将其拆为线性规划的形式。

\((f_{j,k-1}-Sum_j^2)=(-Sum_i)\times (Sum_j)+(f_{i,k})\)

其中四个括号内的内容分别对应 \(y,k,x,b\)。我们的目的是让 \(b\) 最大，即让 \(y\) 轴上的截距最大。我们可以把 \((Sum_j,f_{j,k-1}-Sum_j^2)\) 看作一个点，注意到这个斜率优化的性质很好，不仅横坐标是单增的，斜率还是单减的，下面我们考虑怎样寻找这个 \(b\)。

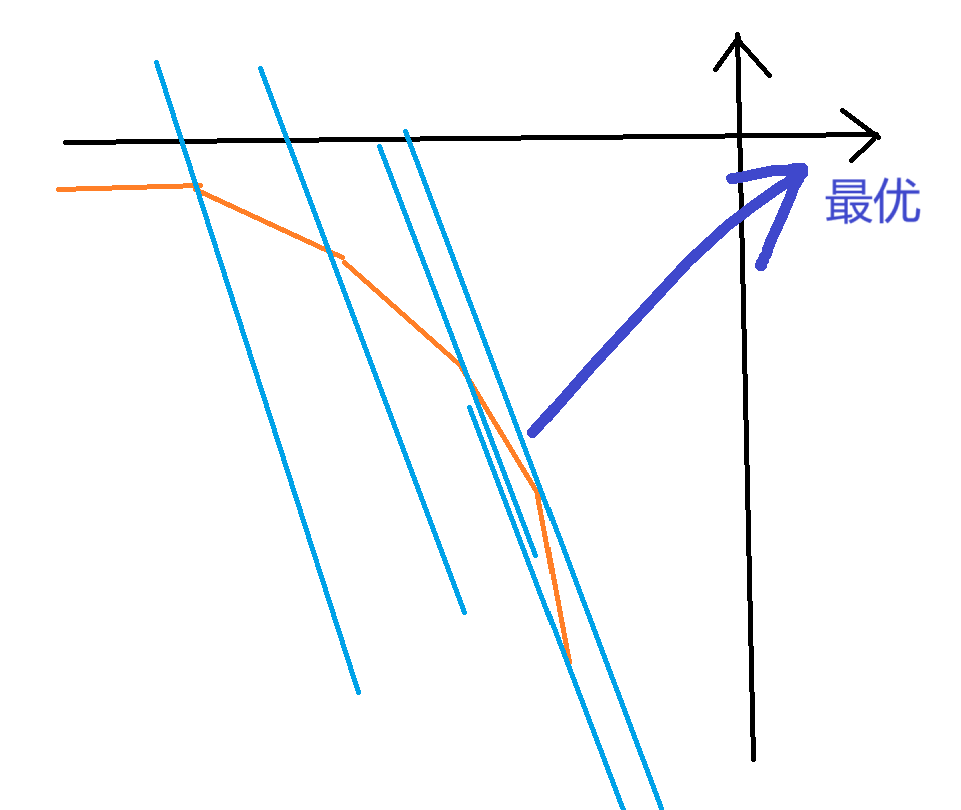
由于 \(k\) 是固定的，所以我们要找的就是前面的所有点引出一个斜率为 \(k\) 的直线，每条直线都对应一个 \(b\)，找寻这些 \(b\) 中最小的一个。那么根据线性规划原理，我们应该切到这些点构成的凸包的 最适点，如图所示，就是凸包上，左边斜率小于它，右边斜率大于它的交界处，这样你把所有浅蓝线画出来之后很容易发现这个是最优的。

于是我们现在要做的就是维护这个凸包，每次找到这个最适点。

上面说过了，由于 \(x\) 是单增的，所以可以直接单调队列维护这个上凸包。而又因为斜率是单减的，我们可以通过弹出队首的方式维护最适点。而若斜率不单增也不困难，我们使用二分队列法（或者也可以叫二分栈因为不弹出队首）即可。

其余两种情况现在还不知道，碰到了再说。

P3195 [HNOI2008] 玩具装箱

首先把那个什么 \(j-i\) 的贡献消了，把 \(C_i\) 全部加 \(1\)，\(L\) 也加 \(1\)。推出来显然有 \(f_i=\min\{f_j+(Sum_i-Sum_j-L)^2\}\)。与上面相同，直接进行分离，\((f_j+Sum_j^2)=(2\times (Sum_i-L)\times Sum_j)+(f_i-(Sum_i-L)^2)\)

注意到 \(k\) 单增，\(x\) 也单增。注意 \(\min\) 维护的是下凸壳，然后直接和上一题一样做就行了。

CF868F Yet Another Minimization Problem

决策单调性分治。这个还挺简单的。当转移不依赖前置状态的选择，或者说转移横向非线性相关时可以使用，常见转移如 \(f_i=\max\{w(j,i)\}\) 或者 \(f_i=\max\{g_j+w(j,i)\}\) 时可以使用，但是一般 \(f_i=\max\{f_j+w(j,i)\}\) 就需要使用斜率优化或者决策单调性二分队列等技巧了。

你可以把决策单调性简单理解为：任意两个待转移点 \(i\) 和 \(j\) 满足 \(i<j\)，如果 \(i\) 的最优决策点 \(p_i\) 和 \(j\) 的最优决策点 \(p_j\) 满足 \(p_i<p_j\)。则称转移满足决策单调性。

决策单调性的严谨证明一般使用四边形不等式。

\(Theory.\) 当贡献函数 \(w(i,j)\) 满足 \(w(i,j)+w(i+1,j+1)\leq w(i,j+1)+w(i+1,j)\)，则其满足四边形不等式，转移满足决策单调性。

一般来说，这种四边形不等式也不会太难证。以此题举例。\(w(i,j)\) 代表 \(i\) 到 \(j\) 区间的相同元素对数。

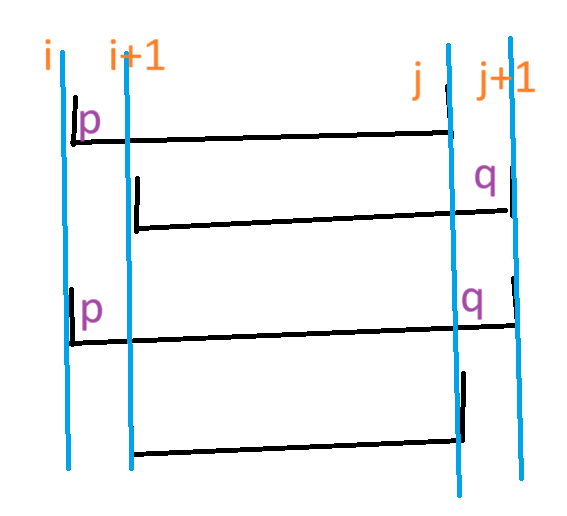
分类讨论。设 \(w(i+1,j)=x\)，设 \([i+1,j]\) 中与 \(p\) 相同的个数为 \(a\)，与 \(q\) 相同的个数为 \(b\)。

若 \(p\neq q\)，则 \(LHS=2x+a+b\)，且 \(RHS=2x+a+b\)，\(LHS= RHS\)，成立。

若 \(p=q\)，则 \(LHS=2x+a+b\)，且 \(RHS=2x+a+b+1\)，\(LHS<RHS\)，成立。

综上 \(w(i,j)+w(i+1,j+1)\leq w(i,j+1)+w(i+1,j)\)，四边形不等式成立。

下面说明决策单调性分治过程：类似整体二分，每次分治在 \(O((r-l)\times polylog)\) 的时间内暴力算出 \(mid\) 的最优决策点 \(p_{mid}\)，则根据决策单调性，\(p_{l\to mid}\leq p_{mid}\)，归入左边分治，\(p_{mid+1\to r}\geq p_{mid}\)，归入右边分治。

若贡献好算，如大部分斜率优化的式子就可以轻而易举的解决，顺便说一句，在按照斜率排序后，斜率优化所维护的式子理论上都要满足决策单调性。

此题中很不幸贡献不好算。你可以考虑以高明手法清空 \(cnt\) 数组然后暴力维护增量转移，这当然没问题，或者你也可以考虑用莫队的形式暴力移动指针，我们可以分析出总的移动次数时 \(O(n\log n)\) 级别的。

下面我们证明移动次数：

\(Proof.\) 使用单点分析法，每个数因为会对答案有贡献，会被算上 \(\log n\) 次，由于分治是有顺序的，所以我们可以认为我们做的移动都是有效移动，即把一个数弹出后，它一定对这次没有贡献，加入后一定有贡献。那么一个数相应也被弹出 \(\log n\) 次，这样总共均摊怎么算都是 \(n\log n\) 级别的。

所以我们就做完了。

[ARC067F] Yakiniku Restaurants

另一种决策单调性。

按照一般解题思路，我们先考虑能不能用多项式复杂度解决题目。那么非常简单，我们设 \(f_{i,j,k}\) 为前 \(i\) 个，目前覆盖区间为 \([j,k]\) 的最大价值。反正只要你能想到一个个加，那多项式复杂度肯定是可以做到的。

太浪费了，我们顺着想能不能去掉一边，我们设 \(f_{i,j}\) 为右端点为 \(i\)，现在到第 \(j\) 个人的最优左端点，这个东西性质非常好（也没有那么好），就是 \(f_{i,j}<f_{i',j}(i<i')\)，感性理解易证（反正我都能理解肯定易证对吧），但是我并不知道以一个点为右端点时，左端点变化对应的图像是什么样的。

上面的式子是层内决策单调性，然后你发现其实也没必要记那个 \(j\) 了，直接变成了 \(f_{i}<f_{i'}(i<i')\)，反正变化也是好维护的。

由于我上面说的：不知道以一个点为右端点时，左端点变化对应的图像是什么样的。所以要是双指针维护这个我也不知道会变成啥样。但是你注意到虽然这个决策单调性是层间的，但是你不依赖前置转移，也就是你前面没有求不出来的东西（\(f_i\) 不依赖 \(f_j\)），那也可以直接上决策单调性分治。

水题做完了。