计算机科学导论-第三版-学习笔记-chapter2-数字系统

 

原本看答案的网站被上保护了，我没账号看不了，开摆。

猜测是那边的学生做作业用chatGPT，部分教师觉得不行，禁止使用的同时把答案都上锁了。

也可能是单纯因为我没报课就没账号。

-------------2023-3-5-------------

学校小道消息，本学期补考可能近日开始，我物化肯定没过，我先去复习一手。

————2023.9.23————

做事还是得有始有终，最近一段时间的笔记一直都在语雀上记。

网站作业啥的就先不管了，大概到国庆的时候吧，我把这章先给搞完吧。

复习题

1.定义一个数字系统。

如果是定义一个数字系统，那么我需要先确认好我要用的数码，再确认我如何用有限的数码来表示数字。

我想定义一个二十进制的数字系统，那么我一共需要二十个各不相同的数码，也就是符号。

A={ 0， 1，  2，  3，  4， 5，  6， 7，  8，  9，

      甲，乙，丙，丁，戊，己，庚，辛，壬，癸}

其中后面的天干十数分别表示十进制中的10、11、12、13、14、15、16、17、18、19.

因为懒得想非位置化的计算法则，所以我这里定义的是一个位置化数字系统。

比如：（甲乙丙丁.5）₂₀=10×20³+11×20²+12×10¹+13×10⁰+5×20^-1=（84533.25）₁₀

　　　（甲乙丙5.丁）₂₀=10×20³+11×20²+12×10¹+5×10⁰+13×20^-1=（84525.65）₁₀

2.辨析位置化和非位置化数字系统。

位置化数字系统，数码在数字中所占据的位置决定其表示的值。如同上文中的（甲乙丙丁.5）₂₀不等于（甲乙丙5.丁）₂₀一般。

而非位置化数字系统，比如罗马数字系统，V=5，I=1，但是IV不等于15而是等于4 。

因为罗马数字系统使用的表示法则不同于位置化法则。

罗马数字系统：（引用自书本）

 

 

 

 

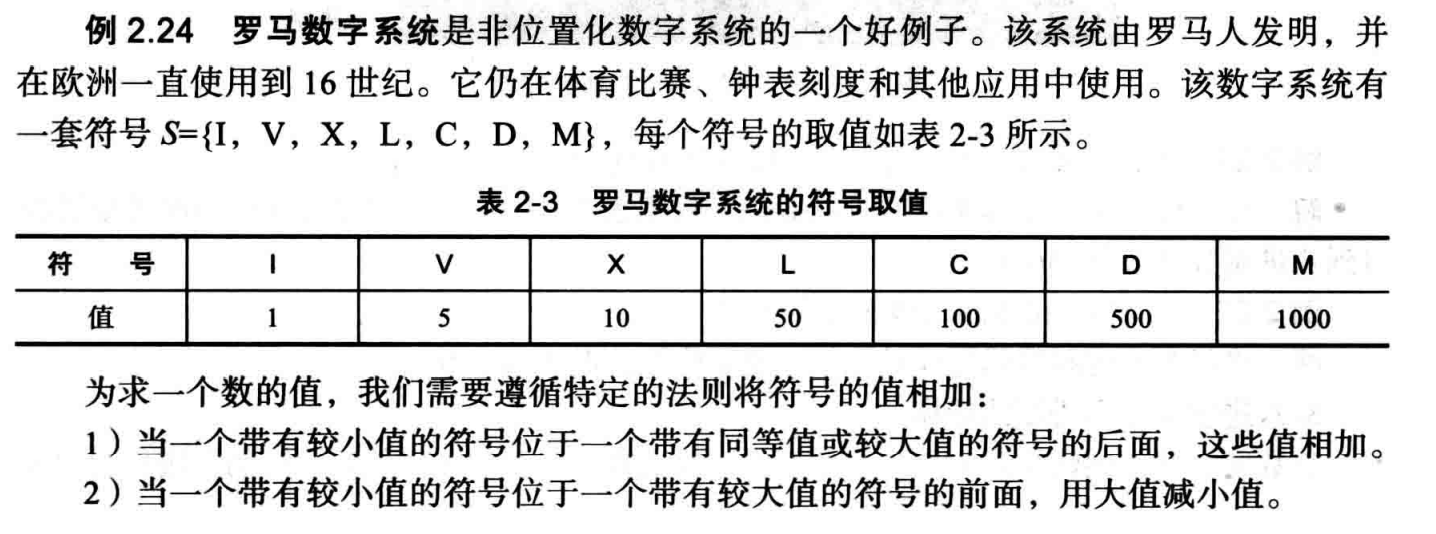
3.定义位置化数字系统中的底或基数。位置化数字系统中，底与符号的数量有什么关系?

-位置化数字系统中的底或基数，就是这系统中所用的有限数码的总数。

　　-比如二进制B={0，1}，底（基数）为二。自然地，上文中的二十进制底就为20了。

　　-严谨一些地说：

　　　　-S是一套数字系统所使用的符号集合

　　　　-b即为S符号集中的符号总数

-那么底与符号数量的关系便是显而易见的了——底 = 符号数量

4.简述十进制系统。为什么称作十进制？该系统的底是多少？

-十进制系统使用十个不同的数码，以位置化数字系统来表示值。十个数码分别为0、1、2、3、4、5、6、7、8、9。

-因为当任一位置的数码由9再增加1时——即达到10时——便要使左边的数码加1，而原本位置的数码变为0。

-十进制系统的底为10

5.简述二进制系统。为什么称作二进制？该系统的底是多少?

-二进制系统使用两个不同的数码，以位置化数字系统来表示值。两个数码分别为0、1。

-因为当任一位置的数码由1再增加1时——即达到$(10)_2$ 时——便要使左边的数码加1，而原本位置的数码变为0。

-二进制系统的底为2

6.简述八进制系统。为什么称作八进制？该系统的底是多少？

-八进制系统使用八个不同的数码，以位置化数字系统来表示值。八个数码分别为0、1、2、3、4、5、6、7。

-因为当任一位置的数码由7再增加1时——即达到$(10)_8$时——便要使左边的数码加1，而原本位置的数码变为0。

-八进制系统的底为8

7.简述十六进制系统。为什么称作十六进制？该系统的底是多少？

-十六进制系统使用十六个不同的数码，以位置化数字系统来表示值。十六个数码分别为0、1、2、3、4、5、6、7、8、9、A、B、C、D、E。

-因为当任一位置的数码由E再增加1时——即达到$(10)_{16}$时——便要使左边的数码加1，而原本位置的数码变为0。

-十六进制系统的底为16

8.为什么二进制和十六进制互换很容易？

-因为十六进制的底（16）是二进制的底（2）的4次方，在这样的情况下——根据进制转换表也能知道——1个1位十六进制数码可以代替对应的4位二进制数码。

9.十六进制系统中1个数码表示二进制系统中的几位？

-4

10.八进制系统中1个数码表示二进制系统中的几位？

-3

附：（进制转换例子）（如有误还请指出。手动计算结果也可以自行使用计算器验证）

 上图中关于1除以2的结果，在整数算术下，商应为0，余数为1，我那里写错了。

 

 练习题 题目的图先不放了，PDF里有

1：[a: 13] [b: 88] [c: 30.25] [d: 63.875]

2: [a: 2738] [b: 291] [c: 2747] [d: 862.87890625]

3：[a:2738] [b:291] [c:2747] [d:862.87890625]

4: [a:10011001000] [b:1011000] [c:1111100.000001...] [d:1110.10001...]

5: [a:2204] [b:143] [c:13.314] [d:110.631...]

6: [a:237] [b:583] [c:C.214] [10.8]

7: [a:14C] [b:109] [c:B.E] [d:2AE.16]

8: [a:2432] [b:2341] [c:273.6] [d:5274.64]

9: [a:15] [b:130] [c:36.2] [d:77.7]

10: [a:D] [b:58] [c:1E.4] [d:3F.E]

11: [a:1111001] [b:1001110] [c:11111111] [d:11010110]

12: [a:11.101] [b:1100.00011] [c:100.001101] [d:1100.0000101]

13: [a:63] [b:99999] [c:16777215] [d:262143]

14: [a:14] [b:4] [c:5]

15: [a:2] [b:3] [c:4]

16: [a:3/16] [b:41/64] [c:13/32] [d:3/8]

17: [a:110.0011] [b:1100.101001] [c:1011.01101] [d:0.011]

18: [a:10的11次方-1] [b:2的13次方-1] [c:8的9次方-1] [d:16的8次方-1]

19: 首先这个题，简单理解一下，应该是限制在底为2、4、8、16的选择中的

因为要是不限制底，都能用一位符号来表示（只要用上的表示数的符号足够多）

这里自然是选底大的来表示，越大的数，底的差距导致的位数差距越明显。

[a:3] [b:5] [c:2] [d:2]