图论记录

CF1187E Tree Painting

给定一棵 \(n\) 个点的树，初始全是白点，每次操作可以选其一染黑，然后获得该白点被染色前所在白色联通块大小的权值。

第一次操作可以任意选点，之后只能选定一个与黑点相邻的白点。

求可获得的最大权值。

\(2 \leq n \leq 2 \times 10^5\)

换根DP。

设 \(f_i\) 表示首先选 \(i\) 染黑时的答案， \(siz_i\) 表示以 \(i\) 为根的子树大小。

考虑节点 \(u\) 向子节点 \(v\) 转移， \(siz'_u = n - siz_v\) ， \(siz'_v = n\) ，有：

\(f_v = f_u - siz_u - siz_v + siz'_u + siz'_v = f_u + n - 2 \times siz_v\)

复杂度 \(O(n)\) 。

/*
 * @Author: FoXreign
 * @Date: 2022-09-20 17:57:32
 */
#include <bits/stdc++.h>
#define IOS                           \
    std::ios::sync_with_stdio(false); \
    std::cin.tie(0);                  \
    std::cout.tie(0);
using PII = std::pair<int, int>;
using ll = long long;
 
int main()
{
    IOS;
    int n;
    std::cin >> n;
    std::vector<std::vector<int>> g(n + 1);
    for (int i = 1, u, v; i < n; ++i)
    {
        std::cin >> u >> v;
        g[u].push_back(v);
        g[v].push_back(u);
    }
    std::vector<ll> f(n + 1);
    std::vector<int> siz(n + 1, 1);
    std::function<void(int, int)> dfs = [&](int u, int fa)
    {
        for (auto v : g[u])
        {
            if (v == fa)
                continue;
            dfs(v, u);
            siz[u] += siz[v];
        }
        f[1] += siz[u];
    };
    dfs(1, 0);
    std::function<void(int, int)> dp = [&](int u, int fa)
    {
        for (auto v : g[u])
        {
            if (v == fa)
                continue;
            f[v] = f[u] + n - 2 * siz[v];
            dp(v, u);
        }
    };
    dp(1, 0);
    ll ans = 0;
    for (int i = 1; i <= n; ++i)
        ans = std::max(ans, f[i]);
    std::cout << ans;
    return 0;
}

CF1204C Anna, Svyatoslav and Maps

给定含 \(n\) 个点的有向无环图，以及由 \(m\) 个点组成的的路径 \(p\) ，在保证 \(p1 \rightarrow p_n\) 最短路仍是 \(p\) 的前提下，你可以删除 \(p_2\) 至 \(p_{n-1}\) 中任意点，问最多可删除多少点。

\(n \leq 100, m \leq 10^6, 1 \leq p_i \leq n\)

保证 \(p_i\) 与 \(p_{i+1}\) 间有一条边相连。

观察到 \(n\) 很小，我们不妨先跑 Floyd 求出任意两点间距。

考虑三元组 \(\{p_i,p_j,p_k\}\) ，如果 \(p_i \rightarrow p_k\) 的最短路与二者下标差相等，则说明 \(p_j\) 是多余的。

实现用到了栈，复杂度 \(O(n^3 + m)\) 。

/*
 * @Author: FoXreign
 * @Date: 2022-09-20 15:24:00
 */
#include <bits/stdc++.h>
#define IOS                           \
    std::ios::sync_with_stdio(false); \
    std::cin.tie(0);                  \
    std::cout.tie(0);
using PII = std::pair<int, int>;
using ll = long long;
const int inf = 0x3f3f3f3f;

int main()
{
    IOS;
    int n, m;
    std::cin >> n;
    std::vector<std::vector<int>> f(n + 1, std::vector<int>(n + 1, inf));
    std::string s;
    for (int i = 1; i <= n; ++i)
        f[i][i] = 0;
    for (int i = 1; i <= n; ++i)
    {
        std::cin >> s;
        for (int j = 1; j <= n; ++j)
            if (s[j - 1] - '0')
                f[i][j] = 1;
    }
    auto Floyd = [&](std::vector<std::vector<int>> &f)
    {
        for (int k = 1; k <= n; k++)
            for (int i = 1; i <= n; ++i)
                for (int j = 1; j <= n; ++j)
                    f[i][j] = std::min(f[i][j], f[i][k] + f[k][j]);
    };
    Floyd(f);
    std::cin >> m;
    std::vector<PII> d(m + 1);
    int r = 0;
    for (int i = 1, p; i <= m; ++i)
    {
        std::cin >> p;
        d[++r] = {p, i};
        while (r >= 3)
        {
            auto x = d[r - 2], y = d[r];
            if (f[x.first][y.first] != y.second - x.second)
                break;
            d[r - 1] = d[r], --r;
        }
    }
    std::vector<int> ans;
    for (int i = 1; i <= r; ++i)
        ans.push_back(d[i].first);
    std::cout << ans.size() << '\n';
    for (auto x : ans)
        std ::cout << x << ' ';
    return 0;
}

CF1249F Maximum Weight Subset

给定一棵含 \(n\) 个节点的树，每个节点有点权 \(a_i\) 。现在要你选出一些节点，使得这些节点的权值和最大且两两之间的距离均大于 \(k\) 。

kls口中的树上背包板题orz

设 \(f_{u,l}\) 表示以节点 \(u\) 为根的子树中，与 \(u\) 的距离大于等于 \(l\) 的最大权值和。

考虑转移，有：

• 选节点 \(u\) ， \(f_{u,0} = a_u + \sum_{v \in son(u)} f_{v,k}\)

• 不选节点 \(u\) ， \(f_{u,l} = max_{v \in son_u}\{ f_{v,l-1} + \sum_{v' \in son(u) \and v' \not = v} f_{v',max\{l-1,k-l\}} \}\)

  \(l-1 + 1 + k - l + 1 = k + 1\) ，保证两两距离大于 \(k\) 。

  距离大于等于 \(l\) ，因此取 \(max\{l-1,k-l\}\) ，同时每一个节点方案处理完转移后要做一个后缀最大值，这样才能保证答案的正确性。

复杂度 \(O(n^4)\) ，但实际上不选时可以预先求和，这样复杂度就降到了 \(O(n^3)\) 。

看了下题解发现还有 \(O(n)\) 的长链剖分做法orz

/*
 * @Author: FoXreign
 * @Date: 2022-09-20 19:41:14
 */
#include <bits/stdc++.h>
#define IOS                           \
    std::ios::sync_with_stdio(false); \
    std::cin.tie(0);                  \
    std::cout.tie(0);
using PII = std::pair<int, int>;
using ll = long long;

int main()
{
    IOS;
    int n, k;
    std::cin >> n >> k;
    std::vector<std::vector<int>> g(n + 1);
    std::vector<int> a(n + 1);
    for (int i = 1; i <= n; ++i)
        std::cin >> a[i];
    for (int i = 1, u, v; i < n; ++i)
    {
        std::cin >> u >> v;
        g[u].push_back(v);
        g[v].push_back(u);
    }
    std::vector<std::vector<ll>> f(n + 1, std::vector<ll>(k + 1));
    std::function<void(int, int)> dp = [&](int u, int fa)
    {
        for (auto v : g[u])
            if (v ^ fa)
                dp(v, u);
        f[u][0] = a[u];
        for (auto v : g[u])
            f[u][0] += f[v][k];
        for (int l = 1; l <= k; ++l)
        {
            int s = 0;
            for (auto v : g[u])
                s += f[v][std::max(l - 1, k - l)];
            for (auto v : g[u])
                f[u][l] = std::max(f[u][l], f[v][l - 1] + s - f[v][std::max(l - 1, k - l)]);
        }
        for (int l = k - 1; l >= 0; --l)
            f[u][l] = std::max(f[u][l], f[u][l + 1]);
    };
    dp(1, 0);
    std::cout << f[1][0];
    return 0;
}

CF1263D Secret Passwords

给定 \(n\) 个字符串

• 如果存在一个或多个字母同时在字符串 \(a\) 和 \(b\) 中出现， \(a\) 和 \(b\) 就被分在同一组
• 如果 \(a\) 和 \(c\) 在同一组， \(b\) 和 \(c\) 在同一组，则 \(a\) 和 \(b\) 也在同一组

问所有的字符串最终被分成几组。

并查集板题。

/*
 * @Author: FoXreign
 * @Date: 2022-09-20 18:16:57
 * @LastEditTime: 2022-09-20 18:29:53
 * @FilePath: \c\Code\graph theory\CF1263D.cpp
 */
#include <bits/stdc++.h>
#define IOS                           \
    std::ios::sync_with_stdio(false); \
    std::cin.tie(0);                  \
    std::cout.tie(0);
using PII = std::pair<int, int>;
using ll = long long;

struct DSU
{
    std::vector<int> fa, size;
    DSU(int n) : fa(n), size(n, 1) { std::iota(fa.begin(), fa.end(), 0); }
    int find(int x)
    {
        while (x != fa[x])
            x = fa[x] = fa[fa[x]];
        return x;
    }
    bool same(int x, int y) { return find(x) == find(y); }
    bool merge(int x, int y)
    {
        x = find(x), y = find(y);
        if (x == y)
            return false;
        if (size[x] > size[y])
            std::swap(x, y);
        fa[x] = y;
        size[y] += size[x];
        return true;
    }
};

int main()
{
    IOS;
    int n;
    std::cin >> n;
    std::vector<bool> vis(26);
    std::vector<std::vector<int>> v(26);
    std::string s;
    for (int i = 1; i <= n; ++i)
    {
        std::fill(vis.begin(), vis.end(), false);
        std::cin >> s;
        for (auto ch : s)
            vis[ch - 'a'] = true;
        for (int j = 0; j < 26; ++j)
            if (vis[j])
                v[j].push_back(i);
    }
    DSU dsu(n + 1);
    for (int i = 0; i < 26; ++i)
        for (int j = 0; j < (int)(v[i].size() - 1); ++j)
            dsu.merge(v[i][j], v[i][j + 1]);
    int ans = 0;
    for (int i = 1; i <= n; ++i)
        if (dsu.fa[i] == i)
            ++ans;
    std::cout << ans;
    return 0;
}

CF1304E 1-Trees and Queries

给定一棵 \(n\) 个点的树,相邻点的距离为 \(1\) 。

\(q\) 个询问，每个询问在原树 \((x,y)\) 间新连上一条边 ，要求判断从 \(a\) 点到 \(b\) 点是否存在距离为 \(k\) 的路径。

\(3 \leq n \leq 10^5，1 \leq q \leq 10^5\)

先假设没有连边的条件， \(a \rightarrow b\) 存在距离为 \(k\) 的路径当前仅当 \(dis(a,b) \geq k\) 且 \(k - dis(a,b)\) 为偶数。

证明很简单，大于 \(k\) 的部分显然可以在终点 \(b\) 旁随便找一个相邻节点来回以 \(2\) 的差消耗掉。

考虑引入边 \((x,y)\) ，其实无非只多了两种可能的情况： \(a \rightarrow x \rightarrow y \rightarrow b\) 与 \(a \rightarrow y \rightarrow x \rightarrow b\) ，用上面相同的条件各判一遍就好。

复杂度 \(O(qlogn)\) 。

/*
 * @Author: FoXreign
 * @Date: 2022-09-21 09:18:40
 */
#include <bits/stdc++.h>
#define IOS                           \
    std::ios::sync_with_stdio(false); \
    std::cin.tie(0);                  \
    std::cout.tie(0);
using PII = std::pair<int, int>;
using ll = long long;

struct HLD
{
    int N;
    std::vector<std::vector<int>> &G;
    std::vector<int> fa, siz, dep, son, top;
    HLD(std::vector<std::vector<int>> &G, int root = 0) : N(G.size()), G(G), fa(N, 0), siz(N, 0), dep(N, 0), son(N, 0), top(N, 0)
    {
        dfs1(root, 0);
        dfs2(root, root);
    };
    void dfs1(int u, int f)
    {
        siz[u] = 1, fa[u] = f, dep[u] = dep[f] + 1;
        for (auto v : G[u])
            if (v != f)
            {
                dfs1(v, u);
                siz[u] += siz[v];
                if (siz[v] > siz[son[u]])
                    son[u] = v;
            }
    }
    void dfs2(int u, int t)
    {
        top[u] = t;
        if (son[u])
            dfs2(son[u], t);
        for (auto v : G[u])
            if (v != fa[u] && v != son[u])
                dfs2(v, v);
    }
    int lca(int x, int y)
    {
        while (top[x] ^ top[y])
        {
            if (dep[top[x]] < dep[top[y]])
                std::swap(x, y);
            x = fa[top[x]];
        }
        if (dep[x] > dep[y])
            std::swap(x, y);
        return x;
    }
};

int main()
{
    IOS;
    int n, q;
    std::cin >> n;
    std::vector<std::vector<int>> g(n + 1);
    for (int i = 1, u, v; i < n; ++i)
    {
        std::cin >> u >> v;
        g[u].push_back(v);
        g[v].push_back(u);
    }
    HLD hld(g, 1);
    auto calc = [&](int a, int b)
    {
        int l = hld.lca(a, b);
        return hld.dep[a] + hld.dep[b] - 2 * hld.dep[l];
    };
    std::cin >> q;
    for (int i = 1, x, y, a, b, k; i <= q; ++i)
    {
        std::cin >> x >> y >> a >> b >> k;
        int dis = calc(a, b);
        if (k >= dis && (k - dis) % 2 == 0)
        {
            std::cout << "YES\n";
            continue;
        }
        dis = calc(a, x) + calc(b, y) + 1;
        if (k >= dis && (k - dis) % 2 == 0)
        {
            std::cout << "YES\n";
            continue;
        }
        dis = calc(b, x) + calc(a, y) + 1;
        if (k >= dis && (k - dis) % 2 == 0)
        {
            std::cout << "YES\n";
            continue;
        }
        std::cout << "NO\n";
    }
    return 0;
}

CF1311E Construct the Binary Tree

要求构造一个 \(n\) 个节点的二叉树，满足所有节点到根的距离之和为 \(d\) 。

\(n \leq 5000, d \leq 5000\)

先判断何时无解，考虑深度和最小与最大，也就是完全二叉树与链的情况，如果此时大于或小于 \(d\) ，必定无解。

否则一定可以通过适当的调整满足条件。

这里是设 \(cnt_i\) 表示深度为 \(i\) 的节点数，初始化为完全二叉树。

不难发现第 \(i\) 层的节点可以移动到下一层当且仅当 \(cnt_{i + 1} + 1 <= 2 \times (cnt_i - 1)\) 。

从浅往深枚举，最后 dfs 编个号输出方案即可。

/*
 * @Author: FoXreign
 * @Date: 2022-09-22 14:37:47
 */
#include <bits/stdc++.h>
#define IOS                           \
    std::ios::sync_with_stdio(false); \
    std::cin.tie(0);                  \
    std::cout.tie(0);
using PII = std::pair<int, int>;
using ll = long long;

void solve()
{
    int n, d, sum = 0;
    std::cin >> n >> d;
    std::vector<int> cnt(d + 1);
    cnt[0] = 1;
    for (int i = 1, m = n - 1; m > 0; ++i)
    {
        cnt[i] = std::min(1 << i, m);
        sum += i * cnt[i];
        m -= 1 << i;
    }
    if (d < sum)
    {
        std::cout << "NO\n";
        return;
    }
    while (d > sum)
    {
        int k = 0;
        for (int i = 1; i <= n; ++i)
        {
            if (!cnt[i])
                break;
            if ((cnt[i + 1] + 1) <= 2 * (cnt[i] - 1))
            {
                k = i;
                break;
            }
        }
        if (!k)
            break;
        ++sum, --cnt[k], ++cnt[k + 1];
    }
    if (sum != d)
    {
        std::cout << "NO\n";
        return;
    }
    std::queue<int> id;
    for (int i = 2; i <= n; ++i)
        id.push(i);
    std::vector<int> ans(n + 1);
    std::function<void(int, int)> dfs = [&](int fa, int dep)
    {
        if (cnt[dep] == 0)
            return;
        --cnt[dep];
        int now = id.front();
        id.pop();
        ans[now] = fa;
        dfs(now, dep + 1);
        dfs(now, dep + 1);
    };
    dfs(1, 1);
    dfs(1, 1);
    std::cout << "YES\n";
    for (int i = 2; i <= n; ++i)
        std::cout << ans[i] << ' ';
    std::cout << '\n';
}

int main()
{
    IOS;
    int t;
    std::cin >> t;
    while (t--)
        solve();
    return 0;
}

CF1322C Instant Noodles

给出一张点数为 \(2n\) 的二分图，右侧第 \(i\) 个点点权为 \(c_i\) 。
令 \(S\) 表示左侧点的一个非空点集，设 \(f(S)\) 表示右侧点中与 \(S\) 相连的点的点权和。
求所有非空集合 \(S\) ， \(f(S)\) 的 \(\gcd\) 。
\(1 \leq n,m \leq 5\times 10^5,1 \leq c_i \leq 10^{12}\)

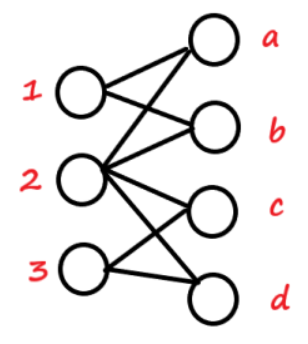
观察上面的样例，由 \(\gcd(a,b) = \gcd(a+b, b)\) 可知，答案为：

\[\begin{align} &\gcd(f(1),f(2),f(3),f(1,2),f(1,3),f(2,3),f(1,2,3)) \\ &= \gcd(a+b,c+d,a+b+c+d)\\ &= \gcd(a+b,c+d) \end{align} \]

可以发现 \(a,b\) 都是与 \(1,2\) 相连， \(c,d\) 都是与 \(3,4\) 相连。

于是大胆猜结论，若右部点 \(i\) 与左部点集 \(|S_1|\) 相连， \(j\) 与左部点集 \(|S_2|\) 相连，当 \(|S_1| = |S_2|\) 时，我们可以将 \(i,j\) 的点权合并。

那么答案就是左部点集相同的右部点点权和的 \(\gcd\) ，实现用 \(STL\) 嵌套哈希，复杂度 \(O(nlogn)\) 加大常数。

/*
 * @Author: FoXreign
 * @Date: 2022-10-07 08:36:24
 */
#include <bits/stdc++.h>
#define IOS                           \
    std::ios::sync_with_stdio(false); \
    std::cin.tie(0);                  \
    std::cout.tie(0);
using PII = std::pair<int, int>;
using ll = long long;

ll solve()
{
    int n, m;
    std::cin >> n >> m;
    std::vector<ll> c(n + 1);
    for (int i = 1; i <= n; ++i)
        std::cin >> c[i];
    std::vector<std::vector<ll>> g(n + 1);
    for (int i = 1, u, v; i <= m; ++i)
    {
        std::cin >> u >> v;
        g[v].push_back(u);
    }
    for (int i = 1; i <= n; ++i)
        std::sort(g[i].begin(), g[i].end());
    std::map<std::vector<ll>, ll> mp;
    for (int i = 1; i <= n; ++i)
        if (!g[i].empty())
            mp[g[i]] += c[i];
    ll res = 0;
    for (auto [x, y] : mp)
        res = std::__gcd(res, y);
    return res;
}

int main()
{
    IOS;
    int t;
    std::cin >> t;
    while (t--)
        std::cout << solve() << '\n';
    return 0;
}

CF1324F Maximum White Subtree

给定一棵 \(n\) 个节点的无根树，每个节点 \(u\) 为黑或白。

对于每个节点 \(u\) ，选出一个包含 \(u\) 的连通子图，设子图中白点个数为 \(cnt_1\) ，黑点个数为 \(cnt_2\) ，要求最大化 \(cnt_1 - cnt_2\) 。

\(1 \leq n \leq 2 \times 10^5\)

由于对每个节点都要求一遍答案，再看下数据范围，基本可以确定是换根DP。

设 \(f_i\) 表示以 \(1\) 为根时的答案， \(g_i\) 表示以 \(i\) 为根的答案，求 \(f_i\) 不过是把序列搬到了树上。

考虑转移， \(g_v = f_v + max\{0, g_u - max\{0, f_v\}\}\) ，经典套路。

复杂度 \(O(n)\) 。

/*
 * @Author: FoXreign
 * @Date: 2022-09-22 19:13:49
 */
#include <bits/stdc++.h>
#define IOS                           \
    std::ios::sync_with_stdio(false); \
    std::cin.tie(0);                  \
    std::cout.tie(0);
using PII = std::pair<int, int>;
using ll = long long;

int main()
{
    IOS;
    int n;
    std::cin >> n;
    std::vector<int> a(n + 1);
    for (int i = 1; i <= n; ++i)
        std::cin >> a[i];
    std::vector<std::vector<int>> g(n + 1);
    for (int i = 1, u, v; i < n; ++i)
    {
        std::cin >> u >> v;
        g[u].push_back(v);
        g[v].push_back(u);
    }
    std::vector<int> f1(n + 1);
    std::function<void(int, int)> dp1 = [&](int u, int fa)
    {
        f1[u] = a[u] ? 1 : -1;
        for (auto v : g[u])
        {
            if (v == fa)
                continue;
            dp1(v, u);
            f1[u] += std::max(0, f1[v]);
        }
    };
    dp1(1, 0);
    auto f2 = f1;
    std::function<void(int, int)> dp2 = [&](int u, int fa)
    {
        for (auto v : g[u])
        {
            if (v == fa)
                continue;
            f2[v] = f1[v] + std::max(0, f2[u] - std::max(0, f1[v]));
            dp2(v, u);
        }
    };
    dp2(1, 0);
    for (int i = 1; i <= n; ++i)
        std::cout << f2[i] << ' ';
    return 0;
}

CF1328E Tree Queries

给定一棵以 \(1\) 为根，含 \(n\) 个节点的树。

有 \(m\) 次询问，每次询问 \(k\) 个节点 ${v_1, v_2 \cdots v_k} $。

求是否存在一条以根节点为一端的链使得询问的每个节点到此链的距离均不大于 \(1\) 。

\(2 \leq n \leq 2 \times 10^5, 1 \leq m \leq 2 \times 10^5\)

在纸上画了画猜了个结论，链的另一端必定是深度最深的点，设其为 \(x\) 。

由于是一棵树，因此 \(v_i\) 到此链的距离等于其到 \(lca(v_i,x)\) 的距离，判断是否均不大于 \(1\) 即可。

/*
 * @Author: FoXreign
 * @Date: 2022-09-23 10:18:44
 */
#include <bits/stdc++.h>
#define IOS                           \
    std::ios::sync_with_stdio(false); \
    std::cin.tie(0);                  \
    std::cout.tie(0);
using PII = std::pair<int, int>;
using ll = long long;

struct HLD
{
    int N;
    std::vector<std::vector<int>> &G;
    std::vector<int> fa, siz, dep, son, top;
    HLD(std::vector<std::vector<int>> &G, int root = 0) : N(G.size()), G(G), fa(N, 0), siz(N, 0), dep(N, 0), son(N, 0), top(N, 0)
    {
        dfs1(root, 0);
        dfs2(root, root);
    };
    void dfs1(int u, int f)
    {
        siz[u] = 1, fa[u] = f, dep[u] = dep[f] + 1;
        for (auto v : G[u])
            if (v != f)
            {
                dfs1(v, u);
                siz[u] += siz[v];
                if (siz[v] > siz[son[u]])
                    son[u] = v;
            }
    }
    void dfs2(int u, int t)
    {
        top[u] = t;
        if (son[u])
            dfs2(son[u], t);
        for (auto v : G[u])
            if (v != fa[u] && v != son[u])
                dfs2(v, v);
    }
    int lca(int x, int y)
    {
        while (top[x] ^ top[y])
        {
            if (dep[top[x]] < dep[top[y]])
                std::swap(x, y);
            x = fa[top[x]];
        }
        if (dep[x] > dep[y])
            std::swap(x, y);
        return x;
    }
};

int main()
{
    IOS;
    int n, m;
    std::cin >> n >> m;
    std::vector<std::vector<int>> g(n + 1);
    for (int i = 1, u, v; i < n; ++i)
    {
        std::cin >> u >> v;
        g[u].push_back(v);
        g[v].push_back(u);
    }
    HLD hld(g, 1);
    std::vector<int> vec(n + 1);
    for (int i = 1, k; i <= m; ++i)
    {
        std::cin >> k;
        for (int j = 1; j <= k; ++j)
            std::cin >> vec[j];
        std::sort(vec.begin() + 1, vec.begin() + k + 1, [&](int x, int y)
                  { return hld.dep[x] > hld.dep[y]; });
        bool flag = true;
        for (int j = 2; j <= k; ++j)
        {
            int l = hld.lca(vec[1], vec[j]);
            int dis = hld.dep[vec[j]] - hld.dep[l];
            if (dis > 1)
            {
                flag = false;
                break;
            }
        }
        std::cout << (flag ? "YES\n" : "NO\n");
    }
    return 0;
}

P3354 河流

给定一棵含 \(n+1\) 个节点，以 \(0\) 为根的树，可以将 \(k\) 个节点设为特殊节点。对于每个点，它产生的花费是它的点权与到最近特殊节点距离的乘积。

求最小花费。

\(2 \leq n \leq 100, 1 \leq k \leq min(n,50)\)

设 \(f_{u,j,k}\) 表示以 \(u\) 为根的子树中已设了 \(k\) 个特殊节点，祖先中最近的特殊节点为 \(j\) 时的最小花费。

这样直接转移复杂度爆炸，因为要枚举子节点分配特殊节点的方案。

考虑多叉树转二叉树，再考虑转移，有：

• 选节点 \(u\) ： \(f_{u,j,k} = \underset{1 \leq l \leq k}{min}\{f_{ls,u,l} + f_{rs,j,k-l-1}\}\)

• 不选节点 \(u\) ： \(f_{u,j,k} = \underset{1 \leq l \leq k}{min}\{f_{ls,j,l} + f_{rs,j,k-l} + w_u \times (d_u - d_j)\}\)

转移时需要注意的是儿子兄弟表示法转换后，右儿子实际上是兄弟节点，第二维要保持一致。

复杂度 \(O(n^4)\) 。

看题解有巨巨说没必要多叉转二叉orz

/*
 * @Author: FoXreign
 * @Date: 2022-09-23 12:19:39
 * @LastEditTime: 2022-09-23 14:09:19
 * @FilePath: \c\Code\graph theory\P3354.cpp
 */
#include <bits/stdc++.h>
#define IOS                           \
    std::ios::sync_with_stdio(false); \
    std::cin.tie(0);                  \
    std::cout.tie(0);
using PII = std::pair<int, int>;
using ll = long long;
const int inf = 0x3f3f3f3f;

int f[105][105][55];

int main()
{
    IOS;
    int n, m;
    std::cin >> n >> m;
    std::vector<int> w(n + 1), v(n + 1), d(n + 1);
    std::vector<std::vector<int>> g(n + 1);
    for (int i = 1; i <= n; ++i)
    {
        std::cin >> w[i] >> v[i] >> d[i];
        g[v[i]].push_back(i);
    }
    std::vector<int> pa(n + 1);
    pa[0] = -1;
    std::vector<std::array<int, 2>> tr(n + 1);
    std::function<void(int)> dfs = [&](int u)
    {
        d[u] += d[v[u]];
        int sz = g[u].size();
        if (!sz)
            return;
        tr[u][0] = g[u][0];
        pa[g[u][0]] = u;
        for (int i = 0; i < sz; ++i)
        {
            dfs(g[u][i]);
            if (i == sz - 1)
                continue;
            tr[g[u][i]][1] = g[u][i + 1];
            pa[g[u][i + 1]] = g[u][i];
        }
    };
    dfs(0);
    memset(f, inf, sizeof(f));
    memset(f[0], 0, sizeof(f[0]));
    std::function<void(int)> dp = [&](int u)
    {
        if (tr[u][0])
            dp(tr[u][0]);
        if (tr[u][1])
            dp(tr[u][1]);
        for (int j = pa[u]; ~j; j = pa[j])
        {
            for (int k = 0; k <= m; ++k)
            {
                for (int l = 0; l <= k; ++l)
                {
                    if (k > l)
                        f[u][j][k] = std::min(f[u][j][k], f[tr[u][0]][u][l] + f[tr[u][1]][j][k - l - 1]);
                    f[u][j][k] = std::min(f[u][j][k], f[tr[u][0]][j][l] + f[tr[u][1]][j][k - l] + w[u] * (d[u] - d[j]));
                }
            }
        }
    };
    dp(0);
    std::cout << f[tr[0][0]][0][m];
    return 0;
}
/*
8 3
5 0 3
7 0 5
3 0 6
9 1 11
8 1 2
1 1 2
2 3 3
4 3 7
87
*/

P2986 Great Cow Gathering G

给定一棵 \(n\) 个节点的无根树，每条边有边权 \(L_i\) ，每个点有点权 \(C_i\) 。选一个节点作为中心点，每个点到中心点的花费为该点点权与路径上边权和的乘积。

求最小花费。

\(1 \leq n \leq 10^5\)

这个题单换根DP板题怎么这么多。。

设 \(num_i\) 表示 \(i\) 为根的子树的点权和， \(f_i\) 表示以 \(i\) 为中心点的答案。

然后转移 \(f_v = f_u + (n - num_v) \times L_{u \rightarrow v} - num_v \times L_{u \rightarrow v} = f_u + (n - 2 \times num_v) * L_{u \rightarrow v}\)

复杂度 \(O(n)\) 。

/*
 * @Author: FoXreign
 * @Date: 2022-09-23 14:42:36
 */
#include <bits/stdc++.h>
#define IOS                           \
    std::ios::sync_with_stdio(false); \
    std::cin.tie(0);                  \
    std::cout.tie(0);
using PII = std::pair<int, int>;
using ll = long long;

int main()
{
    IOS;
    int n;
    std::cin >> n;
    std::vector<int> c(n + 1), num(n + 1);
    for (int i = 1; i <= n; ++i)
        std::cin >> c[i];
    std::vector<std::vector<PII>> g(n + 1);
    for (int i = 1, u, v, w; i < n; ++i)
    {
        std::cin >> u >> v >> w;
        g[u].push_back({v, w});
        g[v].push_back({u, w});
    }
    std::vector<ll> f(n + 1);
    std::function<void(int, int)> dfs = [&](int u, int fa)
    {
        num[u] = c[u];
        for (auto [v, w] : g[u])
        {
            if (v == fa)
                continue;
            dfs(v, u);
            num[u] += num[v];
            f[1] += 1ll * num[v] * w;
        }
    };
    dfs(1, 0);
    std::function<void(int, int)> dp = [&](int u, int fa)
    {
        for (auto [v, w] : g[u])
        {
            if (v == fa)
                continue;
            int tmp = num[1] - num[v];
            f[v] = f[u] + 1ll * (tmp - num[v]) * w;
            dp(v, u);
        }
    };
    dp(1, 0);
    ll ans = 4e18;
    for (int i = 1; i <= n; ++i)
        ans = std::min(ans, f[i]);
    std::cout << ans;
    return 0;
}

CF1369D TediousLee

定义 RDB 为一棵具有特殊性质的树，初始只有一个节点，之后每轮对于该 RDB 中的每个节点 \(x\) ，进行如下操作：

• 如果节点 \(x\) 没有子节点，那么给他加上一个子节点。
• 如果 \(x\) 只有一个子节点，那么给他加上两个子节点。
• 如果 \(x\) 已经有了超过一个子节点，那么我们跳过节点 \(x\) 。

定义一个 claw 为一个中心节点与其三个子节点组成的爪型结构。

给定一个 \(n\) 轮操作后的 RDB ，所有节点初始均为绿色，每次操作可以选择一个绿色的 claw 并将其染为黄色。

求最大染色数。

\(1 \leq n \leq 2 \times 10^6\)

画下图可以发现，第 \(n\) 轮的 RDB 实际上是由一个中心节点挂着两个 \(n-2\) 轮和一个 \(n-1\) 轮的 RDB 构成的，

即： \(f_n = f_{n-1} + 2 \times f_{n-2}\)

然而这样是错的，因为每 \(3\) 轮就会新长出来一个 claw 。

补充上式： \(f_n = f_{n-1} + 2 \times f_{n-2} + 1, n \equiv 0(mod \space 3)\)

/*
 * @Author: FoXreign
 * @Date: 2022-09-25 15:13:46
 */
#include <bits/stdc++.h>
#define IOS                           \
    std::ios::sync_with_stdio(false); \
    std::cin.tie(0);                  \
    std::cout.tie(0);
using PII = std::pair<int, int>;
using ll = long long;
const int N = 2e6 + 5;
const int P = 1e9 + 7;

ll f[N];

int main()
{
    IOS;
    for (int i = 3; i <= 2000000; ++i)
        f[i] = (f[i - 1] + 2ll * f[i - 2] + (i % 3 == 0)) % P;
    int t, n;
    std::cin >> t;
    while (t--)
    {
        std::cin >> n;
        std::cout << 4ll * f[n] % P << '\n';
    }
    return 0;
}

CF1399E1 Weights Division (easy version)

给定一棵含 \(n\) 个节点，以 \(1\) 为根的带权有根树，你可以进行以下操作任意次：

选择任意一条边，令其边权 \(w_i \rightarrow \lfloor \frac{w_i}{2} \rfloor\)

求最小操作数，使得 \(\sum_{v \in leaves} w(root,v) \leq S\)

\(1 \leq n \leq 10^5,1 \leq w_i \leq 10^6\)

预先求出根节点到各叶子结点的路径中，每条边被经过的次数，设其为 \(cnt_i\) 。

那么对其进行操作后，减少的代价为：\((w_i - w_i / 2) \times cnt_i\)

所以用优先队列每次选中影响最大的边操作即可。

复杂度 \(O((n \log w) \log \ (n \log w))\)

/*
 * @Author: FoXreign
 * @Date: 2022-09-25 15:53:19
 */
#include <bits/stdc++.h>
#define IOS                           \
    std::ios::sync_with_stdio(false); \
    std::cin.tie(0);                  \
    std::cout.tie(0);
using ll = long long;
using PII = std::pair<int, int>;

inline ll calc(int w, int sz) { return 1ll * w * sz - 1ll * w / 2 * sz; }

int solve()
{
    int n;
    ll s, now = 0;
    std::cin >> n >> s;
    std::vector<std::vector<std::array<int, 3>>> g(n + 1);
    for (int i = 1, u, v, w, c; i < n; ++i)
    {
        std::cin >> u >> v >> w >> c;
        g[u].push_back({v, w, c});
        g[v].push_back({u, w, c});
    }
    std::priority_queue<std::array<ll, 3>> q1, q2;
    std::vector<int> siz(n + 1); // 叶子个数
    std::function<void(int, int)> dfs = [&](int u, int fa)
    {
        siz[u] = (g[u].size() == 1);
        for (auto [v, w, c] : g[u])
        {
            if (v == fa)
                continue;
            dfs(v, u);
            siz[u] += siz[v];
            now += 1ll * w * siz[v];
            ll val = calc(w, siz[v]);
            if (c == 1)
                q1.push({val, w / 2, siz[v]});
            else
                q2.push({val, w / 2, siz[v]});
        }
    };
    dfs(1, 0);
    if (now <= s)
        return 0;
    std::vector<ll> v1, v2;
    while (!q1.empty())
    {
        auto [x, y, z] = q1.top();
        q1.pop();
        v1.push_back(x);
        x = calc(y, z);
        if (!x)
            continue;
        q1.push({x, y / 2, z});
    }
    while (!q2.empty())
    {
        auto [x, y, z] = q2.top();
        q2.pop();
        v2.push_back(x);
        x = calc(y, z);
        if (!x)
            continue;
        q2.push({x, y / 2, z});
    }
    std::vector<ll> pre1, pre2;
    if (v1.size())
    {
        pre1.push_back(v1[0]);
        for (int i = 1; i < v1.size(); ++i)
            pre1.push_back(pre1[i - 1] + v1[i]);
    }
    if (v2.size())
    {
        pre2.push_back(v2[0]);
        for (int i = 1; i < v2.size(); ++i)
            pre2.push_back(pre2[i - 1] + v2[i]);
    }
    if (v2.empty())
        return 1ll * (std::lower_bound(pre1.begin(), pre1.end(), now - s) - pre1.begin() + 1);
    if (v1.empty())
        return 2ll * (std::lower_bound(pre2.begin(), pre2.end(), now - s) - pre2.begin() + 1);
    auto check = [&](ll x)
    {
        if (x <= 0)
            return 0ll;
        auto it = std::lower_bound(pre2.begin(), pre2.end(), x);
        if (it == pre2.end())
            return 1ll * 0x3f3f3f3f;
        return 2ll * (it - pre2.begin() + 1);
    };
    ll res = check(now - s);
    for (int i = 0; i < v1.size(); ++i)
    {
        ll tmp = check(now - s - pre1[i]) + (i + 1);
        res = std::min(res, tmp);
    }
    return res;
}

int main()
{
    IOS;
    int t;
    std::cin >> t;
    while (t--)
        std::cout << solve() << '\n';
    return 0;
}

CF1399E2 Weights Division (hard version)

给定一棵含 \(n\) 个节点，以 \(1\) 为根的带权有根树，你可以进行以下操作任意次：

选择任意一条边，令其边权 \(w_i \rightarrow \lfloor \frac{w_i}{2} \rfloor\) ，花费为 \(c_i\)

求最小操作数，使得 \(\sum_{v \in leaves} w(root,v) \leq S\)

\(1 \leq n \leq 10^5,1 \leq w_i \leq 10^6,c_i \in \{1,2\}\)

改边有代价，存在后效性，上面的贪心行不通了。

观察到 \(c_i\) 很小，不妨预处理出 \(c_i = 2\) 时的边，再枚举操作多少条 \(c_i = 1\) 的边，最后在 \(c_i = 2\) 的前缀和上二分即可。

/*
 * @Author: FoXreign
 * @Date: 2022-09-25 15:53:19
 */
#include <bits/stdc++.h>
#define IOS                           \
    std::ios::sync_with_stdio(false); \
    std::cin.tie(0);                  \
    std::cout.tie(0);
using ll = long long;
using PII = std::pair<int, int>;

inline ll calc(int w, int sz) { return 1ll * w * sz - 1ll * w / 2 * sz; }

int solve()
{
    int n;
    ll s, now = 0;
    std::cin >> n >> s;
    std::vector<std::vector<std::array<int, 3>>> g(n + 1);
    for (int i = 1, u, v, w, c; i < n; ++i)
    {
        std::cin >> u >> v >> w >> c;
        g[u].push_back({v, w, c});
        g[v].push_back({u, w, c});
    }
    std::priority_queue<std::array<ll, 3>> q1, q2;
    std::vector<int> siz(n + 1); // 叶子个数
    std::function<void(int, int)> dfs = [&](int u, int fa)
    {
        siz[u] = (g[u].size() == 1);
        for (auto [v, w, c] : g[u])
        {
            if (v == fa)
                continue;
            dfs(v, u);
            siz[u] += siz[v];
            now += 1ll * w * siz[v];
            ll val = calc(w, siz[v]);
            if (c == 1)
                q1.push({val, w / 2, siz[v]});
            else
                q2.push({val, w / 2, siz[v]});
        }
    };
    dfs(1, 0);
    if (now <= s)
        return 0;
    std::vector<ll> v1, v2;
    while (!q1.empty())
    {
        auto [x, y, z] = q1.top();
        q1.pop();
        v1.push_back(x);
        x = calc(y, z);
        if (!x)
            continue;
        q1.push({x, y / 2, z});
    }
    while (!q2.empty())
    {
        auto [x, y, z] = q2.top();
        q2.pop();
        v2.push_back(x);
        x = calc(y, z);
        if (!x)
            continue;
        q2.push({x, y / 2, z});
    }
    std::vector<ll> pre1, pre2;
    if (v1.size())
    {
        pre1.push_back(v1[0]);
        for (int i = 1; i < v1.size(); ++i)
            pre1.push_back(pre1[i - 1] + v1[i]);
    }
    if (v2.size())
    {
        pre2.push_back(v2[0]);
        for (int i = 1; i < v2.size(); ++i)
            pre2.push_back(pre2[i - 1] + v2[i]);
    }
    if (v2.empty())
        return 1ll * (std::lower_bound(pre1.begin(), pre1.end(), now - s) - pre1.begin() + 1);
    if (v1.empty())
        return 2ll * (std::lower_bound(pre2.begin(), pre2.end(), now - s) - pre2.begin() + 1);
    auto check = [&](ll x)
    {
        if (x <= 0)
            return 0ll;
        auto it = std::lower_bound(pre2.begin(), pre2.end(), x);
        if (it == pre2.end())
            return 1ll * 0x3f3f3f3f;
        return 2ll * (it - pre2.begin() + 1);
    };
    ll res = check(now - s);
    for (int i = 0; i < v1.size(); ++i)
    {
        ll tmp = check(now - s - pre1[i]) + (i + 1);
        res = std::min(res, tmp);
    }
    return res;
}

int main()
{
    IOS;
    int t;
    std::cin >> t;
    while (t--)
        std::cout << solve() << '\n';
    return 0;
}

CF1388C Uncle Bogdan and Country Happiness

给定一棵含 \(n\) 个节点，根为 \(1\) 的树，对于每个节点 \(i\) ，有 \(p_i\) 个人住在节点 \(i\) 上。

一开始所有人都在根节点上，然后每个人会沿最短路回家。

每个人出发时有一个心情，可能是好心情也可能是坏心情，在经过一条边时，心情可能由好变坏，但是不能由坏变好。

每个点有一个幸福检测器，最后的检测结果为：所有经过该节点的人中，好心情人数与坏心情人数之差 \(h_i\) 。

现给定 \(h_i\) ，问 \(h_i\) 是否合法。

\(1 \leq n \leq 2 \times 10^5,1 \leq \sum_{i = 1}^{n} p_i \leq 10^9\)

考虑自底向上逆推。

设每个节点经过的人数为 \(z_i\) ，其中好心情与坏心情的人数分别为 \(x_i\) 与 \(y_i\) ，显然有以下两个方程：

• \(x_i + y _i = z_i\)
• \(x_i - y_i = h_i\)

由此我们可以推出以下三个结论：

• $ \vert h_i \vert \leq z_i$

• \(y_i = \frac{1}{2} \times (z_i - h_i)\) ，因此 \(z_i - h_i\) 必为偶

• 由于坏心情的不可逆性，它的人数是单调递增的，且增加的人数不会超过住在该节点的人数，即：

  \(z_i - \sum_{j \in son(i)} z_j \leq p_i\)

/*
 * @Author: FoXreign
 * @Date: 2022-09-26 19:40:40
 */
#include <bits/stdc++.h>
#define IOS                           \
    std::ios::sync_with_stdio(false); \
    std::cin.tie(0);                  \
    std::cout.tie(0);
using ll = long long;
using PII = std::pair<int, int>;

bool solve()
{
    int n, m;
    std::cin >> n >> m;
    std::vector<std::vector<int>> g(n + 1);
    std::vector<int> p(n + 1), h(n + 1), siz(n + 1), cnt(n + 1);
    for (int i = 1; i <= n; ++i)
        std::cin >> p[i];
    for (int i = 1; i <= n; ++i)
        std::cin >> h[i];
    for (int i = 1, u, v; i < n; ++i)
    {
        std::cin >> u >> v;
        g[u].push_back(v);
        g[v].push_back(u);
    }
    bool flag = true;
    std::function<void(int, int)> dfs = [&](int u, int fa)
    {
        siz[u] = p[u];
        for (auto v : g[u])
        {
            if (v == fa)
                continue;
            dfs(v, u);
            siz[u] += siz[v], cnt[u] += cnt[v];
        }
        if (abs(h[u]) > siz[u])
        {
            flag = false;
            return;
        }
        if (siz[u] < cnt[u])
        {
            flag = false;
            return;
        }
        if ((siz[u] - h[u]) % 2)
        {
            flag = false;
            return;
        }
        ll tmp = (siz[u] - h[u]) / 2;
        if (tmp - cnt[u] > p[u])
            flag = false;
        cnt[u] = tmp;
    };
    dfs(1, 0);
    return flag;
}

int main()
{
    IOS;
    int t;
    std::cin >> t;
    while (t--)
        std::cout << (solve() ? "YES\n" : "NO\n");
    return 0;
}

CF1387B1 Village (Minimum)

给定一棵含 \(n\) 个节点的无根树，要求你构造一棵同构树，满足映射关系中不存在 \(f(r) = r\) 。

构造的代价为：若 \(f(i) = j\) ，则 \(c_i = dis(i,j)\) ， \(dis(i,j)\) 表示 \(i,j\) 在原树中的距离。

求最小代价与构造方案。

$1 \leq n \leq 10^5 $

显然两个相邻的互换代价最小。

但类似菊花图、奇长链等结构两个一组不可能分完。

因此将剩余的节点划入就近的集合，每个集合对答案的贡献为 \(2 \times (siz_i - 1)\) ， \(siz_i\) 为集合大小。

实现用并查集，复杂度 \(O(nlogn)\) 。

#include <bits/stdc++.h>
#define IOS                           \
    std::ios::sync_with_stdio(false); \
    std::cin.tie(0);                  \
    std::cout.tie(0);
using ll = long long;
using PII = std::pair<int, int>;

struct DSU
{
    std::vector<int> fa, size;
    DSU(int n) : fa(n), size(n, 1) { std::iota(fa.begin(), fa.end(), 0); }
    int find(int x)
    {
        while (x != fa[x])
            x = fa[x] = fa[fa[x]];
        return x;
    }
    bool same(int x, int y) { return find(x) == find(y); }
    bool merge(int x, int y)
    {
        x = find(x), y = find(y);
        if (x == y)
            return false;
        if (size[x] > size[y])
            std::swap(x, y);
        fa[x] = y;
        size[y] += size[x];
        return true;
    }
};

int main()
{
    IOS;
    int n;
    std::cin >> n;
    DSU dsu(n + 1);
    std::vector<int> pa(n + 1), vis(n + 1);
    std::vector<std::vector<int>> g(n + 1);
    for (int i = 1, u, v; i < n; ++i)
    {
        std::cin >> u >> v;
        g[u].push_back(v);
        g[v].push_back(u);
    }
    std::function<void(int, int)> dfs = [&](int u, int fa)
    {
        pa[u] = fa;
        for (auto v : g[u])
            if (v != fa)
                dfs(v, u);
        if (!vis[u] && !vis[fa] && fa)
        {
            vis[u] = vis[fa] = true;
            dsu.merge(u, fa);
        }
    };
    dfs(1, 0);
    if (dsu.size[1] == 1)
        vis[1] = true, dsu.merge(1, g[1][0]);
    std::vector<std::vector<int>> vec(n + 1);
    for (int i = 1; i <= n; ++i)
    {
        if (!vis[i])
            vis[i] = true, dsu.merge(i, pa[i]);
        vec[dsu.fa[i]].push_back(i);
    }
    ll mn = 0;
    std::vector<int> ans(n + 1);
    for (int i = 1; i <= n; ++i)
    {
        if (dsu.fa[i] != i)
            continue;
        mn += 2 * (dsu.size[i] - 1);
        int len = vec[i].size();
        for (int j = 0; j < len; ++j)
            ans[vec[i][j]] = vec[i][(j + 1) % len];
    }
    std::cout << mn << '\n';
    for (int i = 1; i <= n; ++i)
        std::cout << ans[i] << ' ';
    return 0;
}

CF1387B2 Village (Maximum)

给定一棵含 \(n\) 个节点的无根树，要求你构造一棵同构树，满足映射关系中不存在 \(f(r) = r\) 。

构造的代价为：若 \(f(i) = j\) ，则 \(c_i = dis(i,j)\) ， \(dis(i,j)\) 表示 \(i,j\) 在原树中的距离。

求最大代价与构造方案。

$1 \leq n \leq 10^5 $

考虑每条边 \((a,b)\) 对答案的贡献，最大为 \(2 \times min(siz_a,siz_b)\) ，其中 \(siz_i\) 表示以 \(i\) 为根的子树大小。

如果是一条链怎么做，设链上点的编号从浅至深依次为 \(1,2, \cdots , n\) ，那最大代价的划分可以是 \((1,n),(2,n-1),(3,n-2) \cdots\) 以中心点为对称。

对于普遍情况，我们可以先找出树的中心点——树的重心，与重心相连的子树各成一组，然后组与组之间进行交换即可。

简略证明：一条边 \(a,b\) 的贡献在它被经过的次数最多时达到最大，假设 \(siz_a < siz_b\) ，即子树 \(a\) 中所有节点都通过 \((a,b)\) 出去，那子树 \(b\) 中自然会有相应的 \(siz_a\) 个节点进到 \(a\) 中，此时 \((a,b)\) 贡献为 \(2 \times siz_a\) 最大。

因此，只要不同组间互换，本组内的边一定会经历“出去——进来” 的过程，从而使得贡献最大。

复杂度 \(O(n)\) 。

/* 
 * @Author: FoXreign
 * @Date: 2022-09-27 15:27:33
 * @LastEditTime: 2022-09-27 16:24:03
 * @FilePath: \c\Code\graph theory\CF1387B2.cpp
 */
#include <bits/stdc++.h>
#define IOS                           \
    std::ios::sync_with_stdio(false); \
    std::cin.tie(0);                  \
    std::cout.tie(0);
using ll = long long;
using PII = std::pair<int, int>;

int main()
{
    IOS;
    int n, c = 0;
    std::cin >> n;
    std::vector<std::vector<int>> g(n + 1);
    for (int i = 1, u, v; i < n; ++i)
    {
        std::cin >> u >> v;
        g[u].push_back(v);
        g[v].push_back(u);
    }
    std::vector<int> siz(n + 1, 1), w(n + 1);
    std::function<void(int, int)> dfs1 = [&](int u, int fa)
    {
        for (auto v : g[u])
        {
            if (v == fa)
                continue;
            dfs1(v, u);
            siz[u] += siz[v];
            w[u] = std::max(w[u], siz[v]);
        }
        w[u] = std::max(w[u], n - siz[u]);
        if (w[u] <= n / 2)
            c = u;
    };
    dfs1(1, 0);
    ll sum = 0;
    int cnt = 0;
    std::vector<int> ver(n + 1), ans(n + 1);
    std::function<void(int, int)> dfs2 = [&](int u, int fa)
    {
        ver[++cnt] = u;
        for (auto v : g[u])
        {
            if (v == fa)
                continue;
            dfs2(v, u);
            siz[u] += siz[v];
            sum += 2 * std::min(siz[v], n - siz[v]);
        }
    };
    std::fill(siz.begin() + 1, siz.begin() + n + 1, 1);
    dfs2(c, 0);
    for (int i = 1; i <= n / 2; ++i)
    {
        ans[ver[i]] = ver[i + n / 2];
        ans[ver[i + n / 2]] = ver[i];
    }
    if (n & 1)
    {
        ans[ver[1]] = ver[n];
        ans[ver[n]] = ver[1 + n / 2];
        ans[ver[1 + n / 2]] = ver[1];
    }
    std::cout << sum << '\n';
    for (int i = 1; i <= n; ++i)
        std::cout << ans[i] << ' ';
    return 0;
}

CF1385E Directing Edges

给定一个由有向边与无向边组成的图，现在需要你把所有的无向边变成有向边，使得形成的图中没有环。

\(1 \leq n \leq 2 \times 10^5, 1 \leq m \leq min(2 \times 10^5, \frac{n \times (n-1)}{2})\)

先在删掉无向边的图上跑拓扑得到拓扑序，如果最开始就存在环则无解。

之后对于无向边 \((u,v)\) ，如果 \(tfn_u < tfn_v\) ，则 \(u \rightarrow v\) 。

复杂度 \(O(n)\) 。

/*
 * @Author: FoXreign
 * @Date: 2022-09-27 17:15:44
 */
#include <bits/stdc++.h>
#define IOS                           \
    std::ios::sync_with_stdio(false); \
    std::cin.tie(0);                  \
    std::cout.tie(0);
using ll = long long;
using PII = std::pair<int, int>;

void solve()
{
    int n, m, cnt = 0;
    std::cin >> n >> m;
    std::vector<PII> e, ans;
    std::vector<int> in(n + 1), tfn(n + 1);
    std::vector<std::vector<int>> g(n + 1);
    for (int i = 1, t, u, v; i <= m; ++i)
    {
        std::cin >> t >> u >> v;
        if (t == 0)
        {
            e.push_back({u, v});
            continue;
        }
        g[u].push_back(v);
        ans.push_back({u, v});
        ++in[v];
    }
    int tot = n;
    std::queue<int> q;
    for (int i = 1; i <= n; ++i)
        if (!in[i])
            q.push(i);
    while (!q.empty())
    {
        int u = q.front();
        q.pop();
        tfn[u] = ++cnt;
        --tot;
        for (auto v : g[u])
            if (!--in[v])
                q.push(v);
    }
    if (tot)
    {
        std::cout << "NO\n";
        return;
    }
    std::cout << "YES\n";
    for (auto [x, y] : e)
    {
        if (tfn[x] > tfn[y])
            std::swap(x, y);
        ans.push_back({x, y});
    }
    for (auto [x, y] : ans)
        std::cout << x << ' ' << y << '\n';
}

int main()
{
    IOS;
    int t;
    std::cin >> t;
    while (t--)
        solve();
    return 0;
}

CF1383C String Transformation 2

给定两个长为 \(n\) 的字符串 \(A\) 和 \(B\) ，每次可以选取 \(A\) 中若干个相同的字符 \(x\) ，然后将其改成 \(y\) 。

求使得 \(A = B\) 的最小操作次数。

\(1 \leq n \leq 10^5\)

最喜欢的一题

毒瘤题，感觉很多题解都没讲得太明白，后面翻了翻 cf 的评论区，再问了问 hls ，嗯想了一晚上才勉强明白。

原串很长，基本上无从下手。首先要观察到对于两对 \((A_i,B_i),(A_j,B_j)\) ，若 \(A_i = A_j \and B_i = B_j\) ，则 \(i,j\) 是完全等价的，因此我们可以先将字符串问题转化为图论问题，即建立一张包含 \(26\) 个节点的有向图，每个节点分别代表一个字母，对于每对 \((A_i,B_i)\) ，我们连一条从 \(A_i \rightarrow B_i\) 的有向边。

考虑什么情况会使得操作数减少，假设现在存在边 \(a \rightarrow b, \space b \rightarrow c, \space a \rightarrow c\) ，我们可以通过先将所有 \(a\) 更改为 \(b\) ，再将部分 \(b\) 改为 \(c\) 的操作来代替 \(a \rightarrow c\) ，从而省下一次操作。

由此，我们可以大致猜测，最优解由一条长链组成，在这条链中，我们像滚雪球一样将所有的原始字母集中到同一字母中。

如果图中不存在循环，那么这样的雪球就是在 DAG 上跑拓扑排序。但如果存在循环，那么一些节点将被访问不止一次，如 \(A = abcda, B = bdcae\) 。

如果一个顶点无论如何都会被访问不止一次，不妨把它放在顺序中的第一个和最后一个顶点，因为这保证了该顶点可以作为起点达到其它所有顶点，或是作为终点被所有顶点达到。

至于只访问一次的顶点，显然它们之间不可能有任何循环，所以是一个DAG。因此，最优解已经有了一个大致的雏形：访问一些顶点集 \(S\) ，对其余的顶点进行拓扑排序，再次访问 \(S\) 。为了尽量减少操作的数量，我们希望DAG是最大的，即包含的顶点数是最多的。

官方题解在求答案的过程中，引入了WCC，这里复习下WCC的定义，是指同一弱连通分量里的任意两个点 \(x,y\) ，保证至少一方能到达另一方。因此求WCC的个数，应该是先缩点建新图，新图中的每条链即为一个弱连通分量。网上有些博客混淆了弱连通图与弱连通分量的概念。

一个典型的例子： \(x \rightarrow y\) ， \(x \rightarrow z\) ， \(y\) 与 \(z\) 不属于同一WCC。

对一个连通块，最少操作次数为 \(2n - |LDAG| - 1\) ，证明如下：

最初，每个顶点都属于一个单独的WCC，每个DAG由一个顶点组成。所以，有 \(n\) 个WCC，所有DAG的总大小为 \(n\) 。

考虑新加入一条边 \((u,v)\) ：

• 如果 \(u\) 和 \(v\) 在同一个WCC中：如果 \(v\) 在DAG中，则将它从DAG中删除。WCC的数量不变，所有DAG的总大小最多减 \(1\) 。
• 如果 \(u\) 和 \(v\) 在不同的WCC中，那么合并这两个WCC。WCC的数量减少 \(1\) ，DAG的总大小保持不变。

最后，WCC的数量变为 \(1\) ，所以最多合并了 \(n-1\) 次，假设操作了 \(k\) 次，那么就删了 \(k - n + 1\) 个点，所以最终DAG的大小至少是 \(n-(k-n+1)=2n-1-k\) ，即 \(|DAG| \geq 2n - 1- k\) 。

移项得 \(k \geq 2n-1-|DAG|\) ， \(|DAG|\) 最大时 \(k\) 有最小值，和我们上面的推论一致。

这里可能不太好理解的是为什么要引入WCC以及为什么 \(v\) 在DAG中，则将它从DAG中删除。

可以这样想，当加入一条新边 \((u,v)\) 时，发现 \(u,v\) 已在同一WCC中，说明加入这条边后，会形成一个环。但如果我们删掉 \(v\) ，虽然DAG的大小减小了，但一定能保证它还是个DAG。

最后状压DP求最大DAG即可，总复杂度 \(O(2^nn)\) 。

/*
 * @Author: FoXreign
 * @Date: 2022-10-02 18:06:51
 */
#include <bits/stdc++.h>
#define IOS                           \
    std::ios::sync_with_stdio(false); \
    std::cin.tie(0);                  \
    std::cout.tie(0);
using PII = std::pair<int, int>;
using ll = long long;
const int N = 1e5 + 5;
constexpr int ALPHABET_SIZE = 20;

char A[N], B[N];
bool vis[ALPHABET_SIZE];
int reach[ALPHABET_SIZE];

struct DSU
{
    std::vector<int> fa, size;
    DSU(int n) : fa(n), size(n, 1) { std::iota(fa.begin(), fa.end(), 0); }
    int find(int x)
    {
        while (x != fa[x])
            x = fa[x] = fa[fa[x]];
        return x;
    }
    bool same(int x, int y) { return find(x) == find(y); }
    bool merge(int x, int y)
    {
        x = find(x), y = find(y);
        if (x == y)
            return false;
        if (size[x] > size[y])
            std::swap(x, y);
        fa[x] = y;
        size[y] += size[x];
        return true;
    }
};

int solve()
{
    int n;
    scanf("%d", &n);
    scanf("%s", A + 1);
    scanf("%s", B + 1);
    memset(vis, false, sizeof(vis));
    memset(reach, 0, sizeof(reach));
    DSU dsu(20);
    for (int i = 1; i <= n; ++i)
    {
        if (A[i] == B[i])
            continue;
        reach[A[i] - 'a'] |= (1 << (B[i] - 'a'));
        dsu.merge(A[i] - 'a', B[i] - 'a');
    }
    int cnt = 0;
    for (int i = 0; i < ALPHABET_SIZE; ++i)
        if (dsu.fa[i] == i)
            ++cnt;
    int res = 0x3f3f3f3f;
    std::vector<int> f(1 << ALPHABET_SIZE);
    f[0] = 1;
    for (int i = 1; i < (1 << ALPHABET_SIZE); ++i)
        for (int u = 0; u < ALPHABET_SIZE; ++u)
            f[i] |= f[i ^ (1 << u)] && !(reach[u] & i);
    for (int i = 0; i < (1 << ALPHABET_SIZE); ++i)
        if (f[i])
            res = std::min(res, 2 * ALPHABET_SIZE - __builtin_popcount(i) - cnt);
    return res;
}

int main()
{
    int t;
    scanf("%d", &t);
    while (t--)
        printf("%d\n", solve());
    return 0;
}

CF1335F Robots on a Grid

给定一个 \(n\times m\) 的网格，每个格子被染成黑色或白色，并且格子上写有一个方向。

你需要在一些格子中放置机器人，每个时刻机器人会按照当前格子的方向行走一步。要求两个机器人不能同时走到同一格中。

求一个合适的放置方案，使得机器人数量和机器人占据的黑格数量均最多。

\(1 \leq n \times m \leq 10^6\)

从左至右，从上至下编号，根据格子上的方向连边建图。

由于每个点的出度为 \(1\) ，因此环与环间不可能相交。

仅考虑第一问，机器人数量的最大值显然为各环环长之和。

对于第二问，如下图，环中黑格数仅四，但显然在 \(7\) 放和在 \(1\) 放等价，因为它们到 \(3\) 的距离相同。

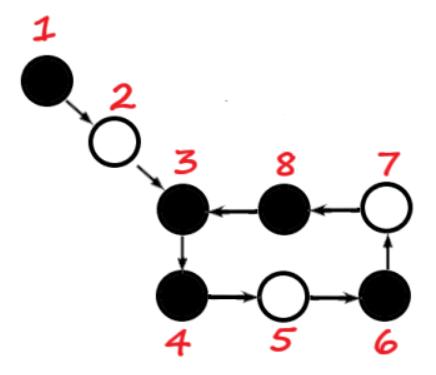
因此我们不妨建反图，从环上任意一点 \(i\) 开始跑 dfs ，如果存在两个点 \(j,k\) 满足：

\(dis(i,j) \space \% \space len = dis(i,k) \space \% \space len\) ，其中 \(len\) 是环长。

那么 \(j,k\) 两点等价。

复杂度 \(O(nm)\) 。

/*
 * @Author: FoXreign
 * @Date: 2022-09-29 20:35:11
 */
#include <bits/stdc++.h>
#define IOS                           \
    std::ios::sync_with_stdio(false); \
    std::cin.tie(0);                  \
    std::cout.tie(0);
#define id(x, y) (((x)-1) * m + (y))
using ll = long long;
using PII = std::pair<int, int>;

void solve()
{
    int n, m;
    std::cin >> n >> m;
    std::string s;
    std::vector<int> col(n * m + 1), vis(n * m + 1), in(n * m + 1), flag(n * m + 1);
    for (int i = 1; i <= n; ++i)
    {
        std::cin >> s;
        for (int j = 1; j <= m; ++j)
            col[id(i, j)] = (s[j - 1] - '0');
    }
    std::vector<std::vector<int>> g(n * m + 1), G(n * m + 1);
    for (int i = 1; i <= n; ++i)
    {
        std::cin >> s;
        for (int j = 1; j <= m; ++j)
        {
            switch (s[j - 1])
            {
            case 'U':
                g[id(i, j)].push_back(id(i - 1, j)), G[id(i - 1, j)].push_back(id(i, j)), ++in[id(i - 1, j)];
                break;
            case 'D':
                g[id(i, j)].push_back(id(i + 1, j)), G[id(i + 1, j)].push_back(id(i, j)), ++in[id(i + 1, j)];
                break;
            case 'L':
                g[id(i, j)].push_back(id(i, j - 1)), G[id(i, j - 1)].push_back(id(i, j)), ++in[id(i, j - 1)];
                break;
            case 'R':
                g[id(i, j)].push_back(id(i, j + 1)), G[id(i, j + 1)].push_back(id(i, j)), ++in[id(i, j + 1)];
                break;
            default:
                break;
            }
        }
    }
    int ans = n * m;
    std::queue<int> q;
    for (int i = 1; i <= n * m; ++i)
        if (!in[i])
            q.push(i);
    while (!q.empty())
    {
        int u = q.front();
        q.pop();
        vis[u] = true;
        --ans;
        for (auto v : g[u])
            if (!--in[v])
                q.push(v);
    }
    std::cout << ans << ' ';
    int sz = 0;
    std::function<void(int)> dfs = [&](int u)
    {
        vis[u] = true;
        for (auto v : g[u])
        {
            if (vis[v])
                continue;
            ++sz;
            dfs(v);
        }
    };
    ans = 0;
    for (int i = 1; i <= n * m; ++i)
    {
        if (vis[i])
            continue;
        sz = 1;
        dfs(i);
        for (int j = 0; j < sz; ++j)
            flag[j] = 0;
        std::queue<PII> q;
        q.push({i, 0});
        while (!q.empty())
        {
            auto [x, z] = q.front();
            q.pop();
            if (col[x] == 0)
                flag[z % sz] = 1;
            for (auto y : G[x])
            {
                if (y == i)
                    continue;
                q.push({y, z + 1});
            }
        }
        for (int j = 0; j < sz; ++j)
            ans += flag[j];
    }
    std::cout << ans << '\n';
}

int main()
{
    IOS;
    int t;
    std::cin >> t;
    while (t--)
        solve();
    return 0;
}

CF1336A Linova and Kingdom

给定 \(n\) 个节点的有根树，根是 \(1\) 号节点，你可以选择 \(k\) 个节点将其设为特殊节点。

每个特殊节点对答案的贡献为其到根的路径经过的普通节点数量。

求最大答案。

\(2\leq n \leq 2\times 10^5,1 \leq k<n\)

考虑选一个点，它带来的贡献是 \(dep_u - siz_u\) ，其中 \(dep_i\) 与 \(siz_i\) 分别表示节点 \(i\) 深度与其子树大小。

贪心即可，复杂度 \(O(nlogn)\) 。

/*
 * @Author: FoXreign
 * @Date: 2022-09-27 20:08:06
 * @LastEditTime: 2022-10-06 16:33:31
 * @FilePath: \c\Code\graph theory\CF1336A.cpp
 */
#include <bits/stdc++.h>
#define IOS                           \
    std::ios::sync_with_stdio(false); \
    std::cin.tie(0);                  \
    std::cout.tie(0);
using ll = long long;
using PII = std::pair<int, int>;

int main()
{
    IOS;
    int n, k;
    std::cin >> n >> k;
    std::vector<int> siz(n + 1, 1), dep(n + 1);
    std::vector<std::vector<int>> g(n + 1);
    for (int i = 1, u, v; i < n; ++i)
    {
        std::cin >> u >> v;
        g[u].push_back(v);
        g[v].push_back(u);
    }
    std::priority_queue<int> pq;
    std::function<void(int, int)> dfs = [&](int u, int fa)
    {
        dep[u] = dep[fa] + 1;
        for (auto v : g[u])
        {
            if (v == fa)
                continue;
            dfs(v, u);
            siz[u] += siz[v];
        }
        pq.push(dep[u] - siz[u]);
    };
    dfs(1, 0);
    ll ans = 0;
    while (k--)
    {
        ans += pq.top();
        pq.pop();
    }
    std::cout << ans;
    return 0;
}

CF1367E Necklace Assembly

给定一个长为 \(n\) 的字符串 \(s\) ，一条项链为一个环，定义一条项链的美丽度为 \(k\) 当且仅当该项链顺时针转 \(k\) 下后与原项链相等。

现给出 \(k\) ，求通过 \(s\) 中的字符组成的最长的美丽度为 \(k\) 的项链。

\(1 \leq n,k \leq 2000\)

顺时针转 \(k\) 下与原串相等，说明循环节长为 \(k\) 的因子。

观察到 \(k\) 很小，不妨枚举 \(k\) 的因子作为循环节长度，再二分求循环节个数即可。

复杂度 \(O(klogn)\) 。

/*
 * @Author: FoXreign
 * @Date: 2022-09-29 14:00:39
 */
#include <bits/stdc++.h>
#define IOS                           \
    std::ios::sync_with_stdio(false); \
    std::cin.tie(0);                  \
    std::cout.tie(0);
using ll = long long;
using PII = std::pair<int, int>;

int solve()
{
    int n, k;
    std::cin >> n >> k;
    std::vector<int> cnt(26);
    std::string s;
    std::cin >> s;
    for (auto ch : s)
        ++cnt[ch - 'a'];
    std::sort(cnt.begin(), cnt.end());
    // x 个长为 y 的循环节
    auto check = [&](int x, int y)
    {
        int tmp = 0;
        for (int i = 0; i < 26; ++i)
            if (cnt[i] >= x)
                tmp += cnt[i] / x;
        return tmp >= y;
    };
    int res = 0;
    for (int i = 1; i <= k; ++i)
    {
        if (k % i)
            continue;
        int l = 1, r = n, mx = 0;
        while (l <= r)
        {
            int mid = l + r >> 1;
            if (check(mid, i))
                l = l + 1, mx = mid;
            else
                r = r - 1;
        }
        res = std::max(res, mx * i);
    }
    return res;
}

int main()
{
    IOS;
    int t;
    std::cin >> t;
    while (t--)
        std::cout << solve() << '\n';
    return 0;
}

CF1361A Johnny and Contribution

给定 \(n\) 个点 \(m\) 条边的无向图。初始点权均为 \(0\) ，每次操作可以将一个点权为 \(0\) 的节点点权重设为 \(x\) ， \(x\) 为点 \(u\) 与其相邻节点 \(v\) 点权的 \(MEX\) 。

求一个操作序列 \(p\) ，使得这样操作后，最终 \(w_i = t_i\) 。

\(1 \leq n,m \leq 5\times 10^5,1 \leq t_i \leq n\)

模拟即可。

/*
 * @Author: FoXreign
 * @Date: 2022-09-29 14:42:48
 * @LastEditTime: 2022-09-29 15:40:45
 * @FilePath: \c\Code\graph theory\CF1361A.cpp
 */
#include <bits/stdc++.h>
#define IOS                           \
    std::ios::sync_with_stdio(false); \
    std::cin.tie(0);                  \
    std::cout.tie(0);
using ll = long long;
using PII = std::pair<int, int>;

int main()
{
    IOS;
    int n, m;
    std::cin >> n >> m;
    std::vector<std::vector<int>> g(n + 1), vec(n + 1);
    for (int i = 1, u, v; i <= m; ++i)
    {
        std::cin >> u >> v;
        g[u].push_back(v);
        g[v].push_back(u);
    }
    std::vector<int> t(n + 1), vis(n + 1);
    for (int i = 1; i <= n; ++i)
    {
        std::cin >> t[i];
        vec[t[i]].push_back(i);
    }
    std::vector<int> ans;
    for (int i = 1; i <= n; ++i)
    {
        if (vec.empty())
            continue;
        for (int j = 0; j < (int)vec[i].size(); ++j)
        {
            int u = vec[i][j];
            if (vis[u] == t[u] - 1)
            {
                ans.push_back(u);
                for (auto v : g[u])
                {
                    if (t[u] == t[v])
                    {
                        std::cout << -1;
                        exit(0);
                    }
                    if (vis[v] == t[u] - 1)
                        ++vis[v];
                }
            }
        }
    }
    if (ans.size() != n)
    {
        std::cout << -1;
        return 0;
    }
    for (auto x : ans)
        std::cout << x << ' ';
    return 0;
}

CF1343E Weights Distributing

给出一个有 \(n\) 个点， \(m\) 条边的无向图和一个长为 \(m\) 的权值序列 \(w\) 。

你可以随意安排边权（每条边权对应 \(w\) 中的一个数，不可重复）。

求 \(a\) 到 \(b\) 的最短路与 \(b\) 到 \(c\) 的最短路的和的最小值。

$2 \leq n \leq 2 \times 10^5 , n-1 \le m \le min(\frac{n(n-1)}{2},2 \times 10^5) $

首先只考虑 \(a \rightarrow b\) 的最短路，只需做一次 bfs ，再选前 \(dis(a,b)\) 小的 \(w\) 即可。

然后有个很显然的结论：\(b \rightarrow c\) 经过的中转点必在 \(a \rightarrow b\) 的路径上。

等同于求点 \(d\) ，令路径 \(a \rightarrow d \rightarrow b \rightarrow d \rightarrow c\) 的长度最小，即 \(dis(a,d) + 2 \times dis(b,d) + dis(d,c)\) 最小。

因此先以 \(a,b,c\) 为起点分别做三次 bfs ，之后再枚举点 \(d\) 求最小值就好。

复杂度 \(O(n)\) 。

/*
 * @Author: FoXreign
 * @Date: 2022-09-29 17:03:28
 */
#include <bits/stdc++.h>
#define IOS                           \
    std::ios::sync_with_stdio(false); \
    std::cin.tie(0);                  \
    std::cout.tie(0);
using ll = long long;
using PII = std::pair<int, int>;
const int inf = 0x3f3f3f3f;

ll solve()
{
    int n, m, a, b, c;
    std::cin >> n >> m >> a >> b >> c;
    std::vector<int> p(m + 1);
    for (int i = 1; i <= m; ++i)
        std::cin >> p[i];
    std::sort(p.begin() + 1, p.begin() + m + 1);
    std::vector<ll> sum(m + 1);
    for (int i = 1; i <= m; ++i)
        sum[i] = sum[i - 1] + p[i];
    std::vector<std::vector<int>> g(n + 1);
    for (int i = 1, u, v; i <= m; ++i)
    {
        std::cin >> u >> v;
        g[u].push_back(v);
        g[v].push_back(u);
    }
    auto bfs = [&](int s)
    {
        std::vector<int> dis(n + 1, inf);
        dis[s] = 0;
        std::queue<int> q;
        q.push(s);
        while (!q.empty())
        {
            int u = q.front();
            q.pop();
            for (auto v : g[u])
            {
                if (dis[v] > dis[u] + 1)
                {
                    dis[v] = dis[u] + 1;
                    q.push(v);
                }
            }
        }
        return dis;
    };
    auto disa = bfs(a), disb = bfs(b), disc = bfs(c);
    ll res = std::numeric_limits<ll>::max();
    for (int i = 1; i <= n; ++i)
    {
        int x = disa[i], y = disb[i], z = disc[i];
        if (x + y + z <= m)
            res = std::min(res, 2ll * sum[y] + sum[x + y] - sum[y] + sum[x + y + z] - sum[x + y]);
    }
    return res;
}

int main()
{
    IOS;
    int t;
    std::cin >> t;
    while (t--)
        std::cout << solve() << '\n';
    return 0;
}

CF1401D Maximum Distributed Tree

给定一棵 \(n\) 个节点的树，编号为 \(1,2 \cdots n\) 。你可以给每条树边赋边权，当且仅当满足以下条件：

• 每条边权均为正整数

• 边权的 乘积 等于 \(k\)

• 边权为 \(1\) 的边数量尽可能少

定义 \(f(u,v)\) 表示节点 \(u\) 到节点 \(v\) 的简单路径经过的边权总和。求 \(\sum\limits_{i=1}^{n-1}\sum\limits_{j=i+1}^{n} f(i,j)\) 的最大值。

\(2 \leq n \leq 10^6, 1 \leq m \leq 6 \times 10^4, 2 \leq p_i \leq 6 \times 10^4, k = \prod\limits_{i=1}^m p_i\) ， \(p_i\) 为质数。

最直白的想法就是一条边被经过的次数越多，填的边权就应越大。

考虑边 \((a,b)\) ， 对子树 \(a\) 中编号为 \(i\) 的节点，假设 \(b\) 中有 \(x\) 个小于 \(i\) 的节点， \(y\) 个大于 \(i\) 的节点。

那根据定义，求 \(f(i,j)\) 时 \(i\) 出去要经过 \(y\) 次边 \((a,b)\) ， \(b\) 中小于 \(i\) 的 \(x\) 个点求 \(f(j,i)\) 时进来经过 \(x\) 次边 \((a,b)\) ，即 \(x + y = siz_b\) 次。

因此边 \((a,b)\) 被经过的总次数为 \(siz_a \times siz_b\) 。

最后讨论下 \(m\) 与 \(n-1\) 的关系， \(m \leq n-1\) 时，为了满足条件二三，从大到小顺着填就好。

\(m > n-1\) 时，把前 \(m - n + 1\) 大的乘起来即可，注意乘的时候不要取模。

/*
 * @Author: FoXreign
 * @Date: 2022-09-28 11:19:16
 */
#include <bits/stdc++.h>
#define IOS                           \
    std::ios::sync_with_stdio(false); \
    std::cin.tie(0);                  \
    std::cout.tie(0);
using ll = long long;
using PII = std::pair<int, int>;
const int P = 1e9 + 7;

ll solve()
{
    int n, m;
    std::cin >> n;
    std::vector<int> siz(n + 1, 1);
    std::vector<std::vector<int>> g(n + 1);
    for (int i = 1, u, v; i < n; ++i)
    {
        std::cin >> u >> v;
        g[u].push_back(v);
        g[v].push_back(u);
    }
    std::cin >> m;
    std::vector<ll> p(m + 1);
    for (int i = 1; i <= m; ++i)
        std::cin >> p[i];
    std::sort(p.rbegin(), p.rbegin() + m);
    std::function<void(int, int)> dfs = [&](int u, int fa)
    {
        for (auto v : g[u])
        {
            if (v == fa)
                continue;
            dfs(v, u);
            siz[u] += siz[v];
        }
    };
    dfs(1, 0);
    std::priority_queue<ll> q;
    for (int i = 2; i <= n; ++i)
        q.push(1ll * siz[i] * (n - siz[i]));
    int id = std::max(0, m - (n - 1)) + 1;
    for (int i = 1; i < id; ++i)
        p[id] = p[id] * p[i] % P;
    ll res = 0;
    for (int i = id; i <= m; ++i)
    {
        res = (res + (q.top() * p[i]) % P) % P;
        q.pop();
    }
    while (!q.empty())
    {
        res = (res + q.top()) % P;
        q.pop();
    }
    return res;
}

int main()
{
    IOS;
    int t;
    std::cin >> t;
    while (t--)
        std::cout << solve() << '\n';
    return 0;
}

End

很菜，很多题都不能一眼秒。

换根 DP 有点像在 DP 上 DP ，考虑换根时带来的影响。

和距离有关的 DP 一般来说有一维和最近的xx相关。

和点权、边权有关的题多从每条边、每个点的贡献考虑。

题目选自 Div. 3难度图论树论题练手 。