2024-03-20 leetcode写题记录
2024-03-20 leetcode写题记录
23. 合并 K 个升序链表
题目链接
题意
给你一个链表数组,每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中,返回合并后的链表。
节点定义如下:
struct ListNode {
int val;
ListNode *next;
ListNode() : val(0), next(nullptr) {}
ListNode(int x) : val(x), next(nullptr) {}
ListNode(int x, ListNode *next) : val(x), next(next) {}
};
解法
用优先队列维护下先后顺序就行,注意lambda函数的写法和优先队列自定义排序方式的写法。
class Solution {
public:
ListNode *mergeKLists(vector<ListNode *> &lists) {
auto cmp = [](ListNode *a, ListNode *b) {
if (a == nullptr) return true;
if (b == nullptr) return false;
return a->val > b->val;
};
priority_queue<ListNode *, vector<ListNode *>, decltype(cmp)> p(cmp);
for (ListNode *x : lists) p.push(x);
ListNode *last = nullptr, *x = nullptr, *head = nullptr;
while (!p.empty() && p.top() != nullptr) {
x = p.top();
p.pop();
if (last == nullptr)
head = x;
else
last->next = x;
last = x;
p.push(x->next);
}
return head;
}
};
4. 寻找两个正序数组的中位数
题目链接
题意
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为 O(log (m+n)) 。
解法
因为时间复杂度要求为O(log(m+n)),所以要将两个数组一起二分,每次的“mid”在这里是两个数,这就让简单的二分变得非常复杂,边界情况比较多。
首先可以将问题做初步的简化,中位数因为有两种情况(总数为奇数和总数为偶数),这里可以转化到另一个求第k大的问题上,对于偶数情况,调用两次求第k大的函数取平均就行。
对于求第k大,当两个数组a和b的元素个数比较平均时,我们考虑两个数组里各自下标为(k-1)/2的元素,分别记为x1和x2,当x1小于x2时,且k为奇数时,a数组的前(k-1)/2-1个元素一定不是要求的第k大,而当k为偶数时,a数组的前(k-1)/2个元素一定不是要求的第k大(可以思考下极限情况)。
而当a和b的元素个数不够平均时,比如说a有2个,b有7个,以
k=5
a=[1, 2]
b=[3, 4, 5, 6, 7, 8, 9]
为例,(k-1)/2为2,但是a数组只有2个元素,下标到不了2,这时可以取a里下标为1,b里下标为2的元素,这样上面的性质仍然成立。
由于每次判断一次之后,a数组或者b数组中的元素会减少,所以我们需要用l1和l2来维护数组的起始位置,当其中一个数组只有一个元素时就可以返回了(即循环里判断的\(k==1\)、\(l1==n1-1\)和\(l2==n2-1\))。
class Solution {
public:
int findk(vector<int>& a1, vector<int>& a2, int k) {
int n1 = a1.size(), n2 = a2.size(), l1 = 0, l2 = 0;
while (true) {
int m = (k - 1) / 2, idx1, idx2;
if (l1 + m >= n1) {
idx1 = n1 - 1;
idx2 = k - n1 + l1 - 1;
} else if (l2 + m >= n2) {
idx2 = n2 - 1;
idx1 = k - n2 + l2 - 1;
} else {
idx1 = l1 + m;
idx2 = l2 + m;
}
if (a1[idx1] < a2[idx2]) {
if (k == 1) return a1[idx1];
if (l1 == n1 - 1) return a2[idx2];
int last = l1;
if (k & 1 || idx1 == n1 - 1)
l1 = idx1;
else
l1 = idx1 + 1;
k -= l1 - last;
} else {
if (k == 1) return a2[idx2];
if (l2 == n2 - 1) return a1[idx1];
int last = l2;
if (k & 1 || idx2 == n2 - 1)
l2 = idx2;
else
l2 = idx2 + 1;
k -= l2 - last;
}
}
}
double findMedianSortedArrays(vector<int>& a1, vector<int>& a2) {
int n1 = a1.size(), n2 = a2.size();
if (n1 == 0) {
if (n2 & 1) return a2[n2 / 2];
return (a2[n2 / 2 - 1] + a2[n2 / 2]) / 2.0;
} else if (n2 == 0) {
if (n1 & 1) return a1[n1 / 2];
return (a1[n1 / 2 - 1] + a1[n1 / 2]) / 2.0;
}
if ((n1 + n2) & 1) return findk(a1, a2, (n1 + n2) / 2 + 1);
return (findk(a1, a2, (n1 + n2) / 2) + findk(a1, a2, (n1 + n2) / 2 + 1)) / 2.0;
}
};
25. K 个一组翻转链表
题目链接
题意
给你链表的头节点 head ,每 k 个节点一组进行翻转,请你返回修改后的链表。
k 是一个正整数,它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍,那么请将最后剩余的节点保持原有顺序。
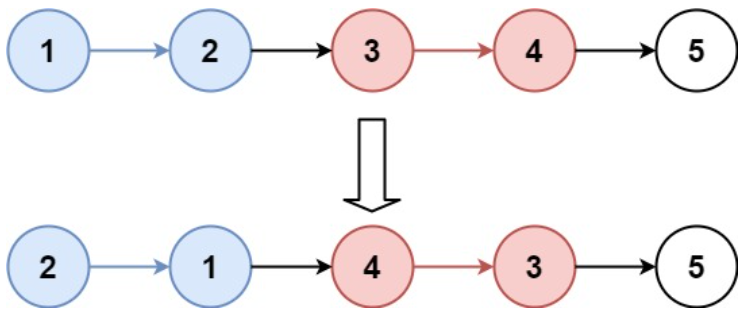
节点定义如下:
struct ListNode {
int val;
ListNode* next;
ListNode() : val(0), next(nullptr) {}
ListNode(int x) : val(x), next(nullptr) {}
ListNode(int x, ListNode* next) : val(x), next(next) {}
};
解法
纯模拟,每k个一组进行反转。
class Solution {
public:
ListNode* reverseKGroup(ListNode* head, int k) {
ListNode *last = nullptr, *next = nullptr;
ListNode *l = head, *r = nullptr;
ListNode *now = nullptr, *tmp = nullptr, *lastt = nullptr;
while (true) {
int cnt = k - 1;
r = l;
while (r != nullptr && cnt) r = r->next, cnt--;
if (cnt != 0 || r == nullptr) break;
next = r->next;
now = l;
r->next = nullptr;
lastt = nullptr;
while (now != nullptr) {
tmp = now->next;
now->next = (lastt == nullptr) ? next : lastt;
lastt = now;
now = tmp;
}
if (last == nullptr)
head = r;
else
last->next = r;
last = l;
l = next;
}
return head;
}
};
25. 188. 买卖股票的最佳时机 IV
题目链接
题意
给你一个整数数组 prices 和一个整数 k ,其中 prices[i] 是某支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。也就是说,你最多可以买 k 次,卖 k 次。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
解法
简单的动态规划。
class Solution {
public:
int maxProfit(int k, vector<int>& prices) {
vector<int> buy(k + 1, INT_MIN), sell(k + 1, 0);
for (int& x : prices)
for (int i = 1; i <= k; ++i) {
buy[i] = max(buy[i], sell[i - 1] - x);
sell[i] = max(sell[i], buy[i] + x);
}
return sell[k];
}
};


 浙公网安备 33010602011771号
浙公网安备 33010602011771号