卡特兰数

卡特兰数：

通项：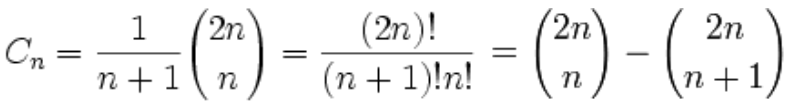

递推式：

代码：

void Catalan(){
	f[0] = f[1] = 1;
	for(int i=2;i<N;i++){
		f[i] = 0;
		for(int j=0;j<=i;j++)
			f[i] += f[j]  * f[i-j-1];
	}
}

模型求解：

1. 出栈次序

   • 设x为当前出栈序列的最后一个，则x有n种取值。

   • 由于x是最后一个出栈的，所以可以将已经出栈的数分成两部分：比x小，比x大。

   • 比x小的数有个，所以这些数的全部出栈可能为

   • 比x大的数有个，所以这些数的全部出栈可能为

   • 这两部分互相影响，所以一个x的取值能够得到的所有可能性为

   • 

2. 合法的括号序列
   • 左右括号分别对应入栈和出栈
3. 不经过对角线的非降路径数
   • 右上分别代表出栈和入栈
4. 二叉树个数
   • 确定根结点，左右个数划分
5. 凸多边形三角划分
   • 以边为基准，随机找一点，构成三角形。则k把三角形分成和
6. 找零问题。有2n个人排成一行进入剧场。入场费 5 元。其中只有n个人有一张 5 元钞票，另外n人只有 10 元钞票，剧院无其它钞票，问有多少中方法使得只要有 10 元的人买票，售票处就有 5 元的钞票找零？
   • 设5为入栈，10为出栈 
7. 圆上不相交。在圆上有2n个点，将这些点成对连接起来使得所得到的n条线段不相交的方法数？
   • 设基准点为A为0，则与A相连的点k必定为奇数编号点（否则无法一边会产生孤立点）。
   • 点k分n为两部分和
   • 
   • 。结合递归式，不难发现