第三章:多维随机变量及其分布
3.1.1 二维随机变量及其分布函数
二维随机变量定义

联合分布函数
x,y的联合分布函数
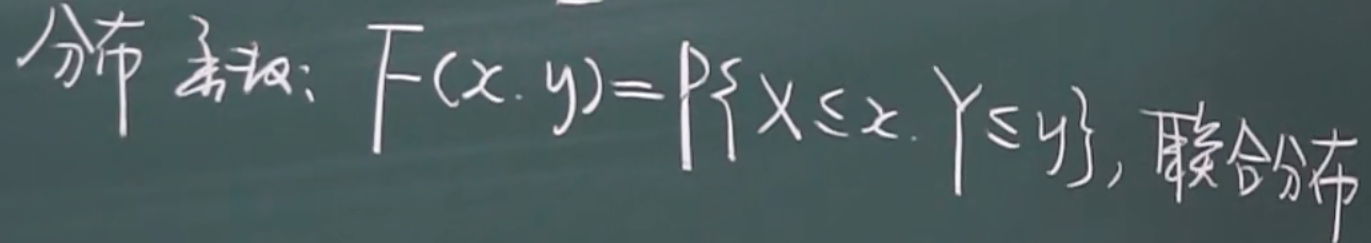
对比
一维
曲线是概率密度函数
负无穷到x 上 的面积是分布函数的函数值
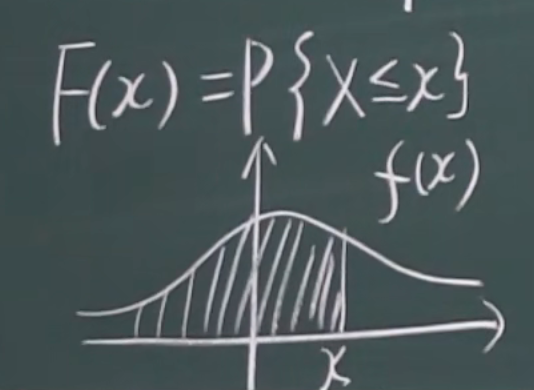
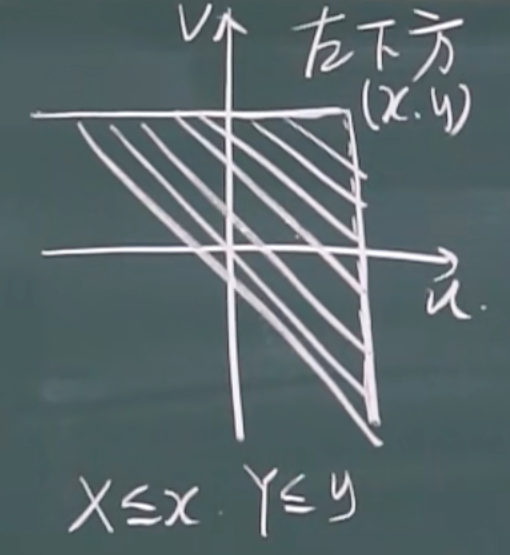
二维
定义域
曲面是概率密度函数
x,y围成面积 上 的体积是分布函数的函数值
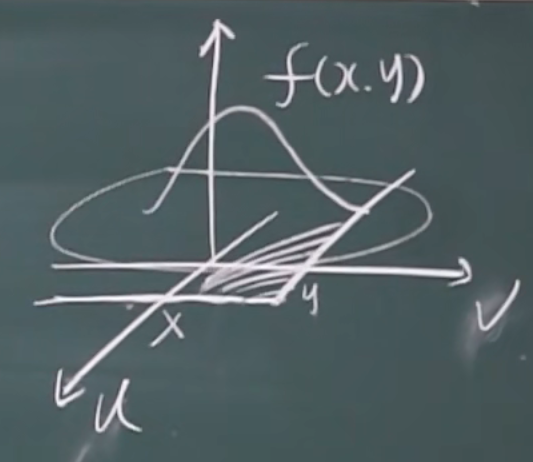
性质
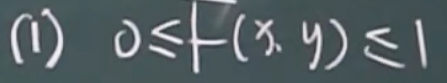
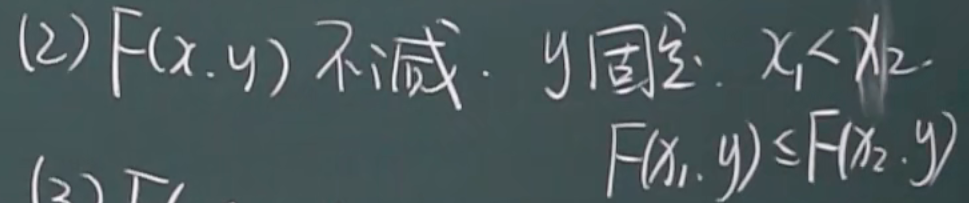
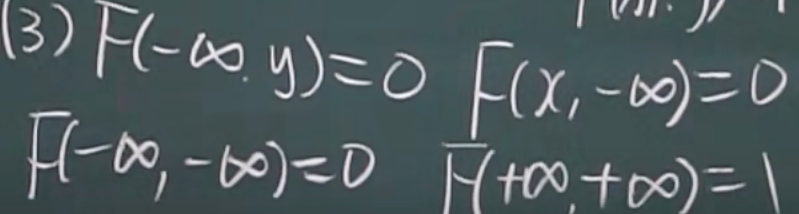
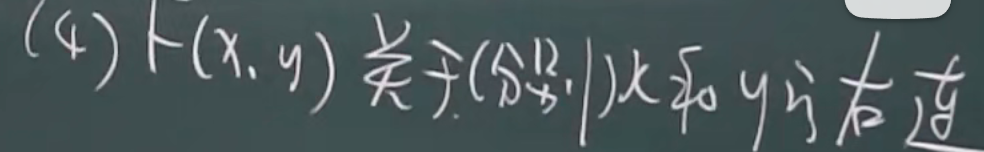
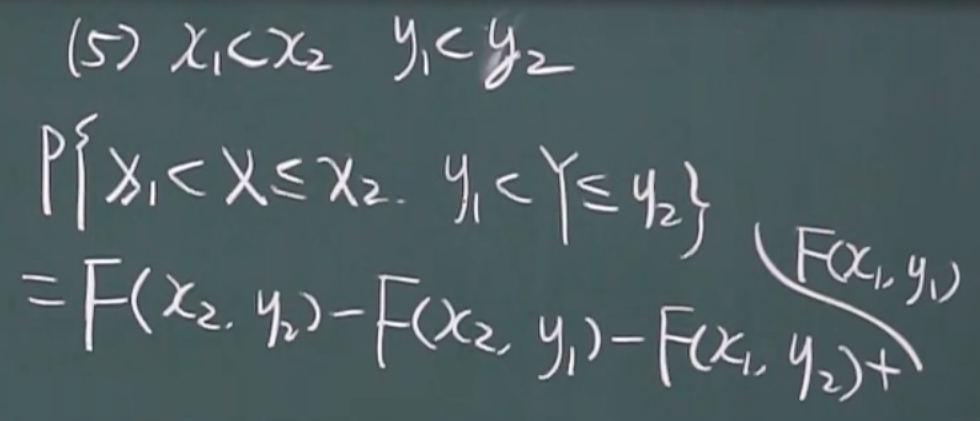
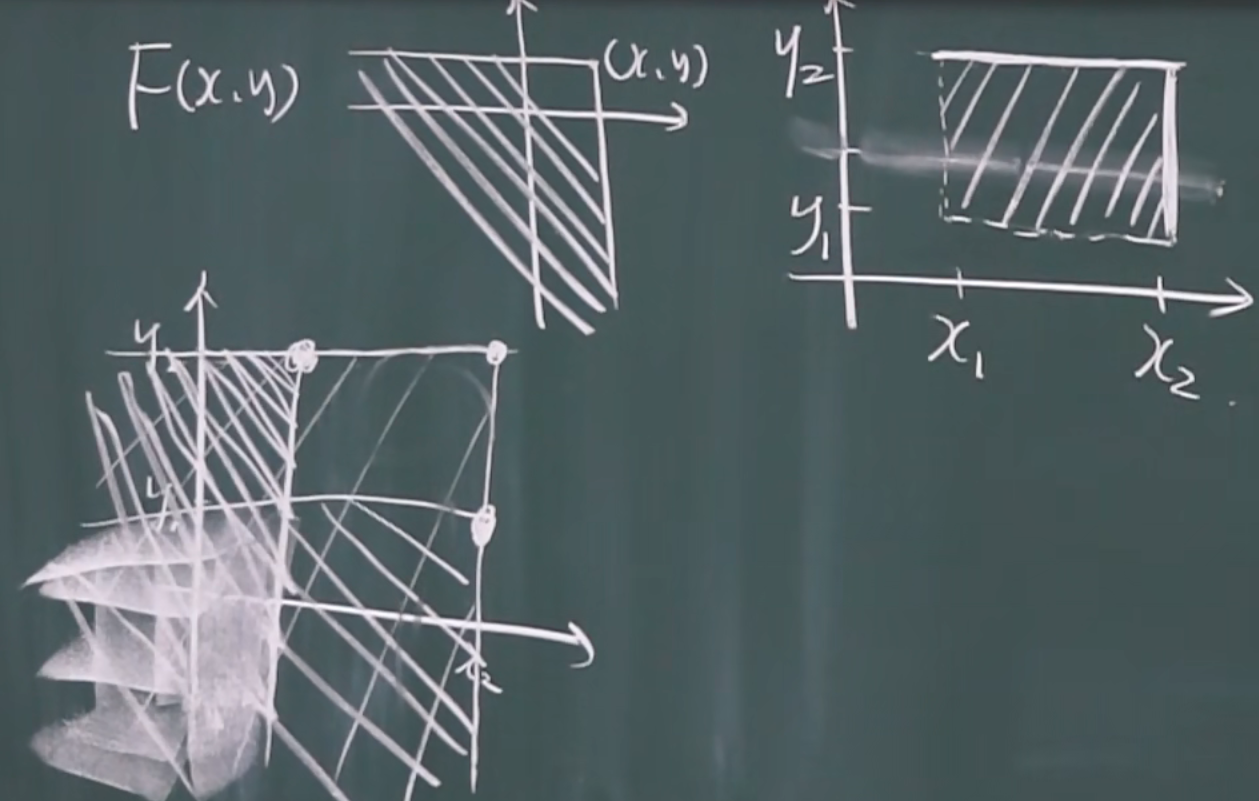
边缘分布函数
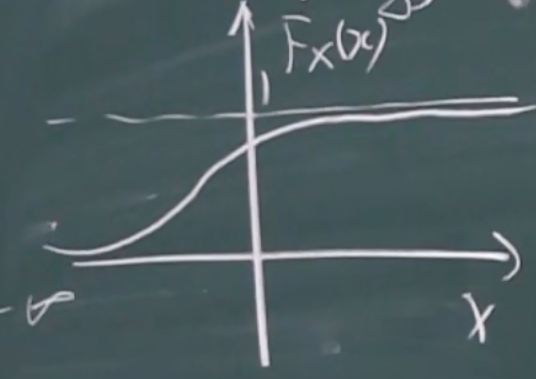
x的边缘分布
y随便取(取y的所有值)
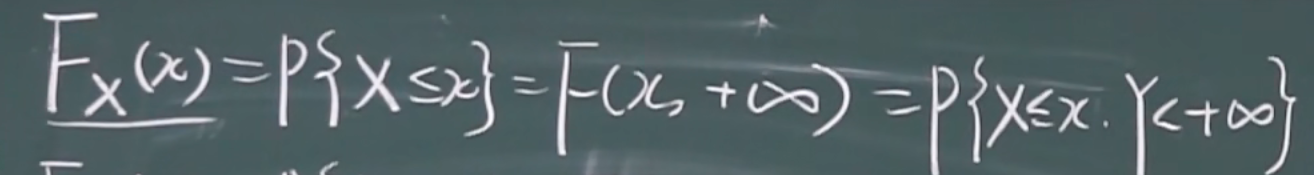
示例:一个垂直于x轴的平面从负无穷逐渐向外移动,移动过程中切到的体积越来越大
y的边缘分布
x随便取(取x的所有值)
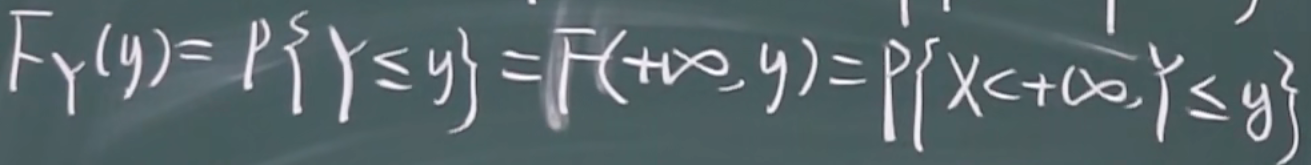
3.1.2 二维 离散型 的联合分布和边缘分布
联合分布函数
联合分布表
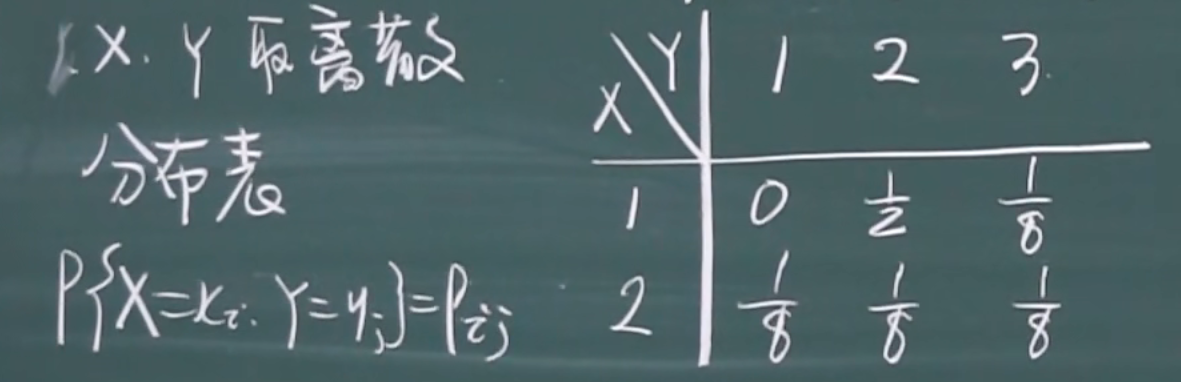
联合分布表的性质
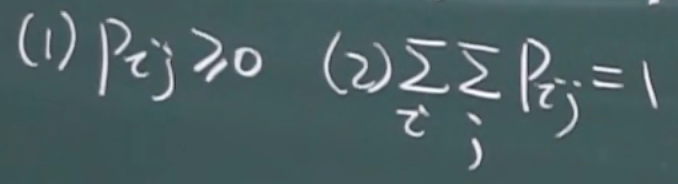
求联合分布函数
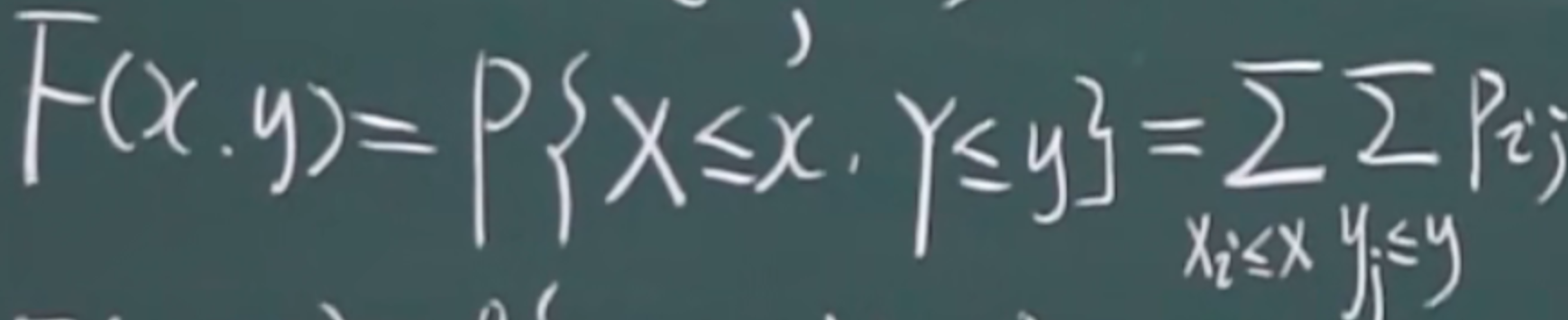
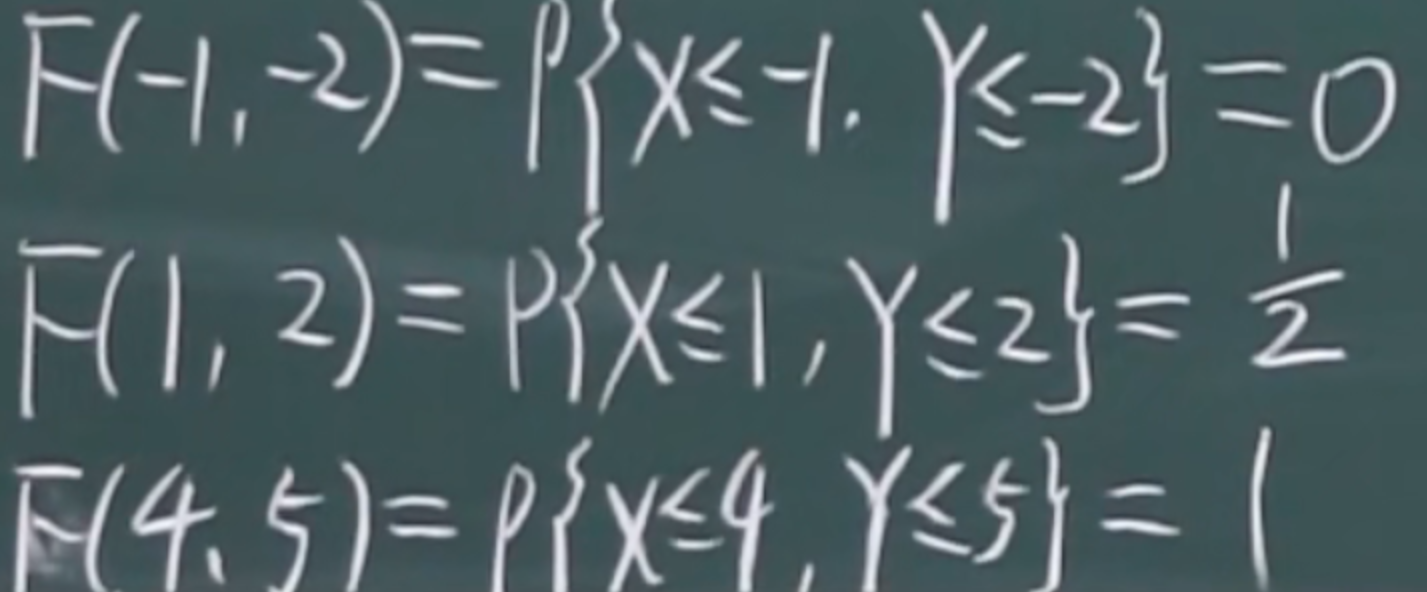
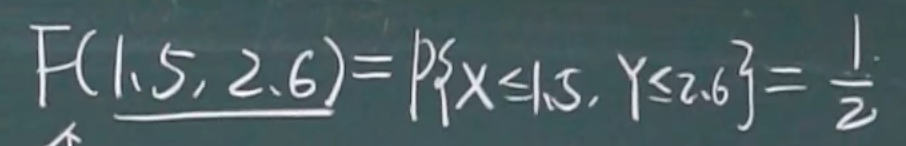
边缘分布函数
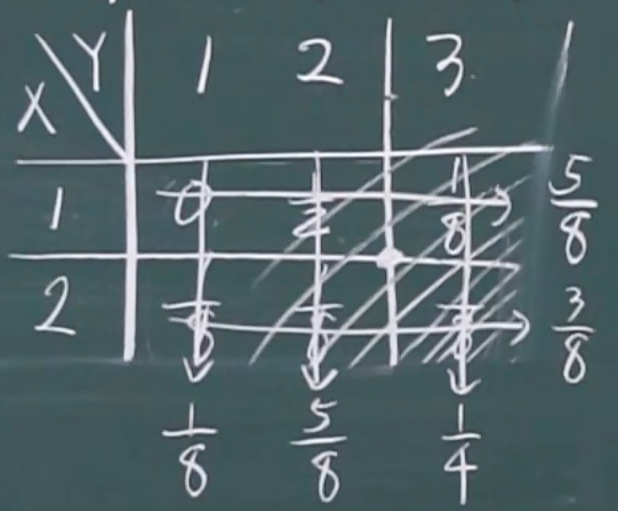
对行求和,得到x的边缘分布
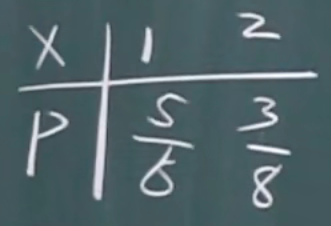
对列求和,得到y的边缘分布
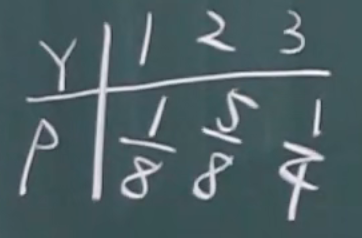

x,y独立时可由边缘分布确定联合分布
3.1.3 二维 连续性 的联合分布和边缘分布
联合分布函数
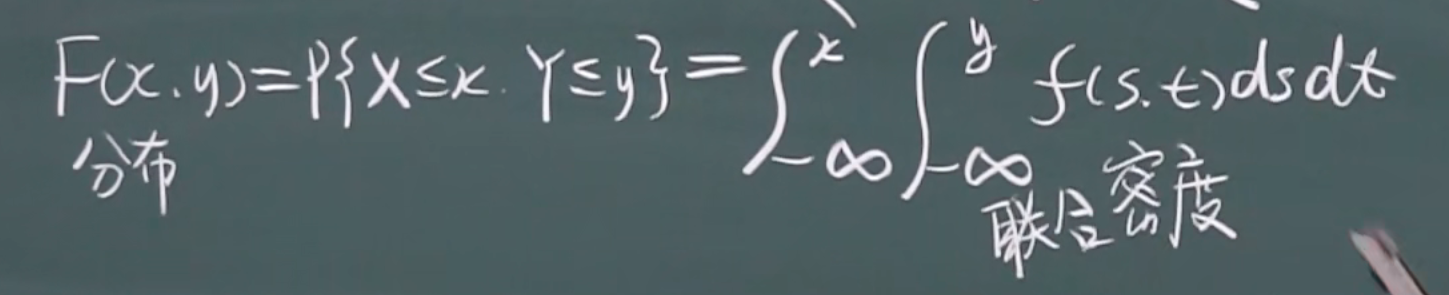
联合密度(一个曲面)

性质
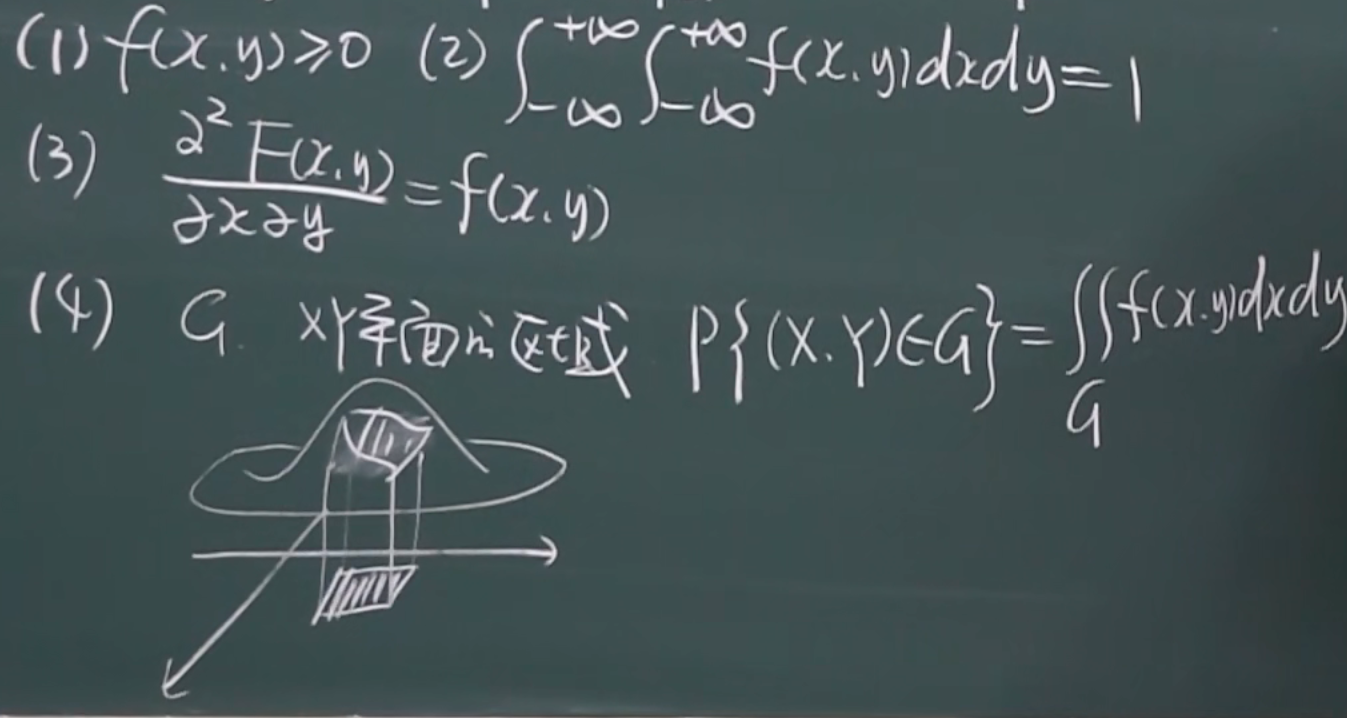
例题
1.求c
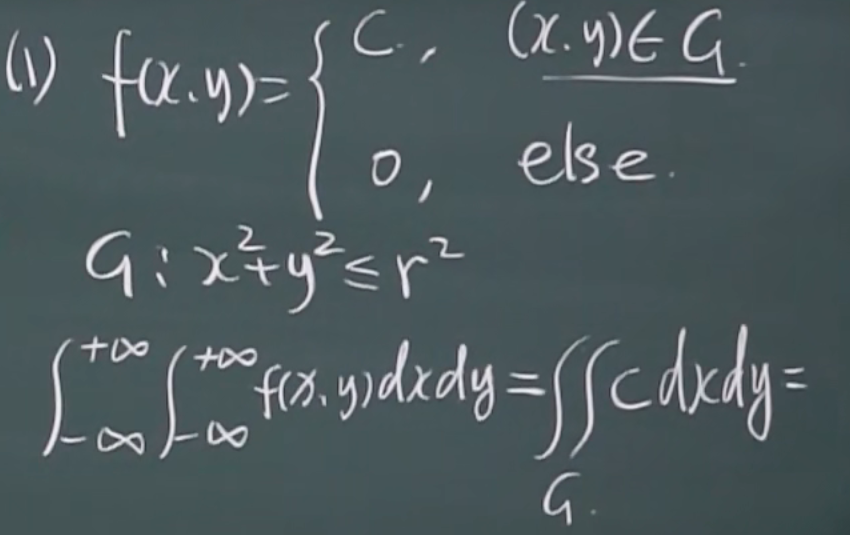
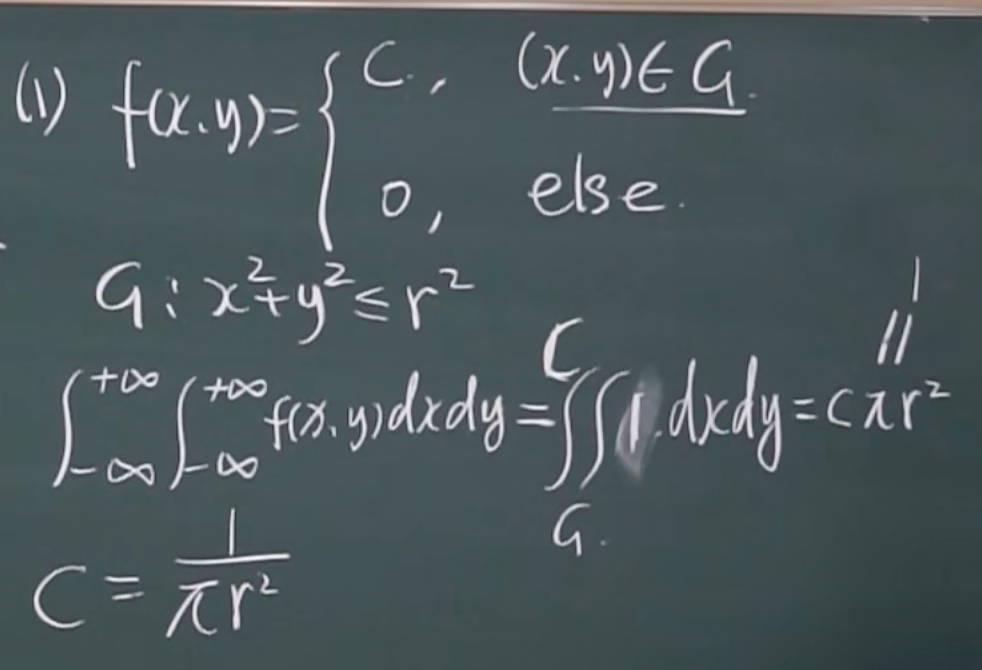
上面是实线,下面是虚线
均匀分布(二维)
G是有界区域
2.(常规题型)
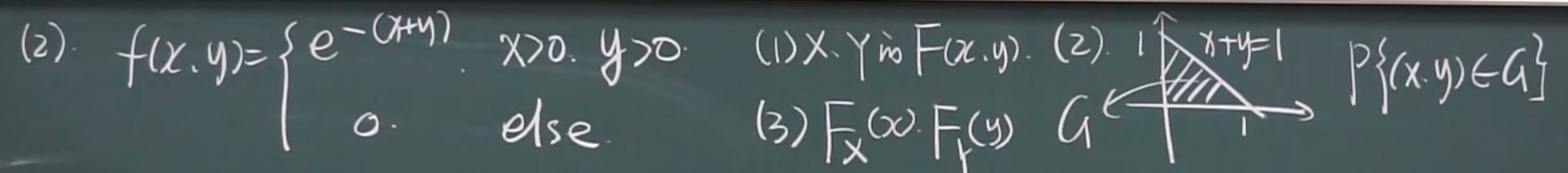
(1)
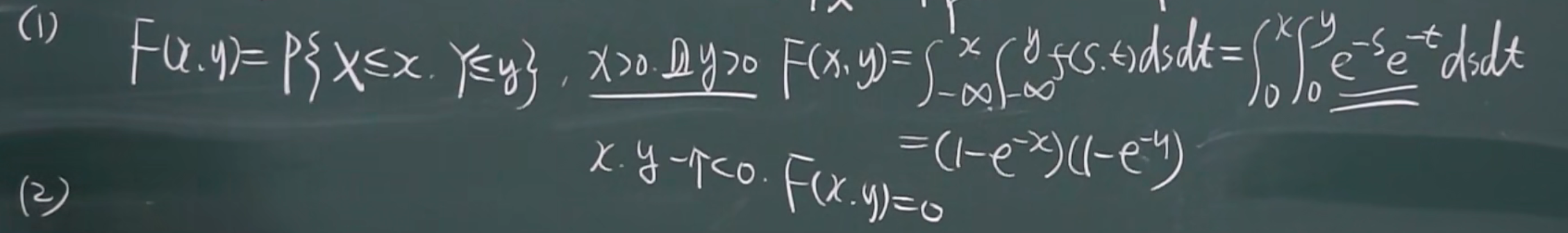
中间步骤
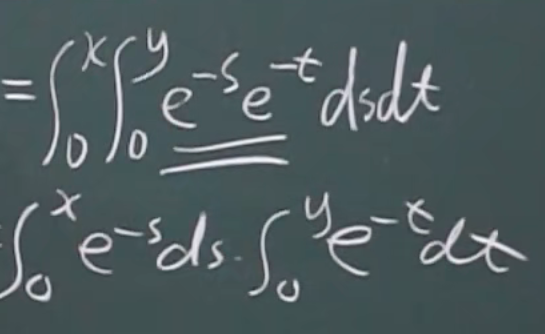
(2)
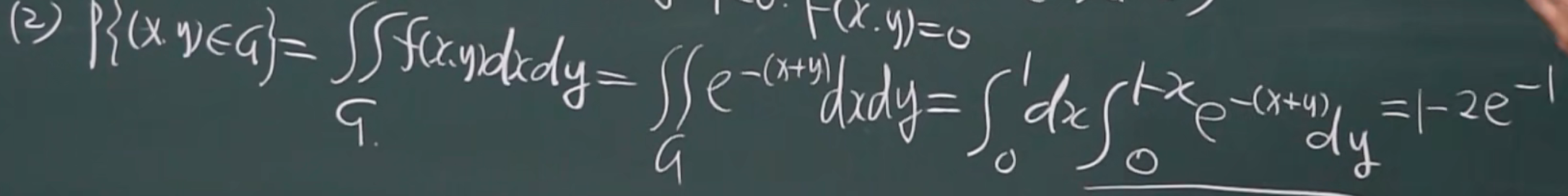
计算过程:
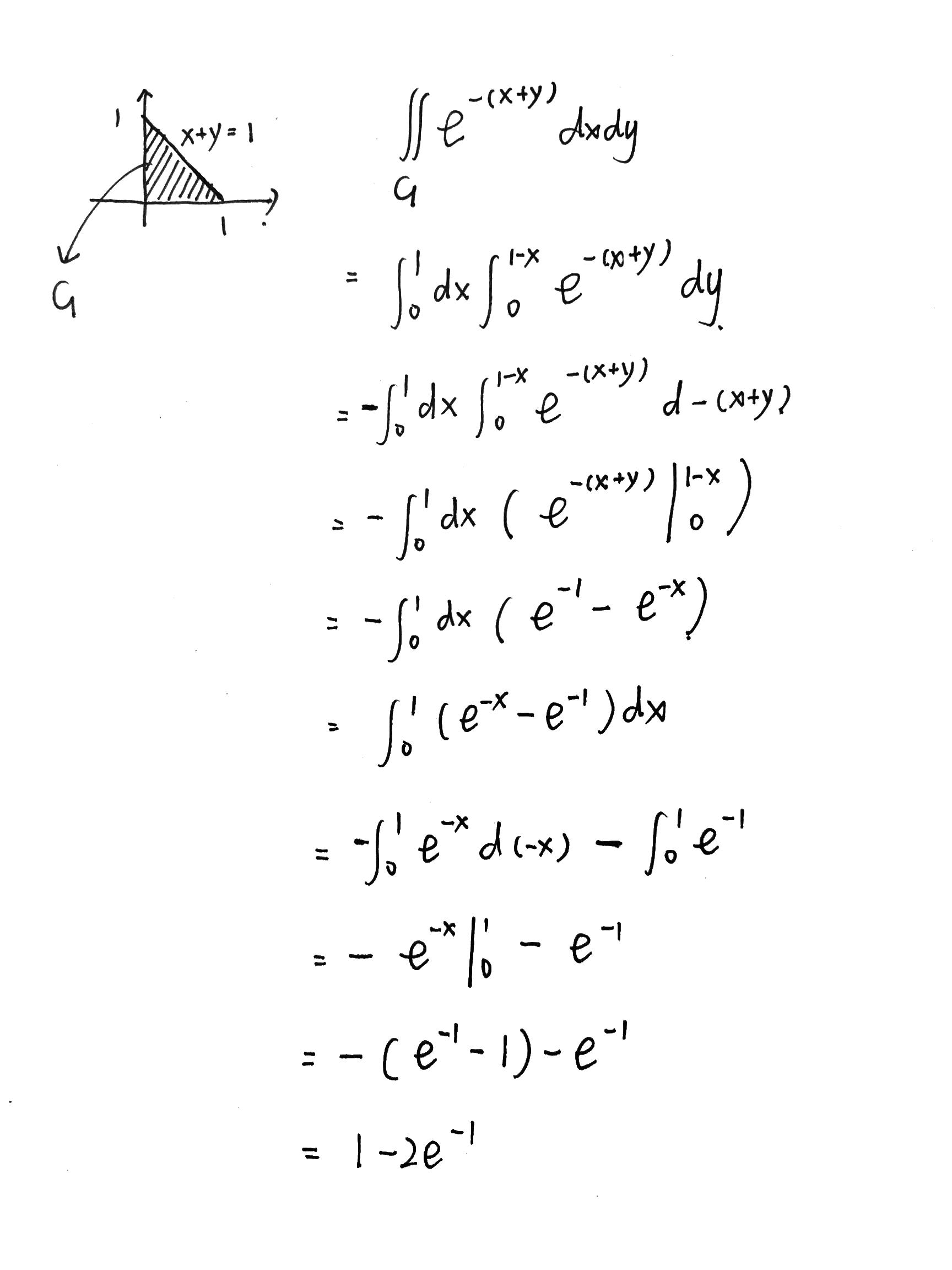
(3)
x>0
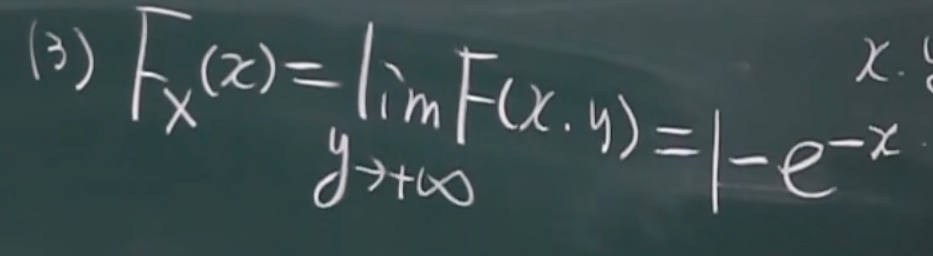
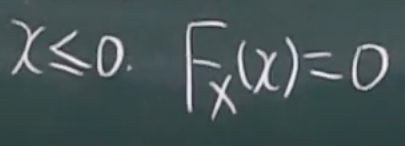
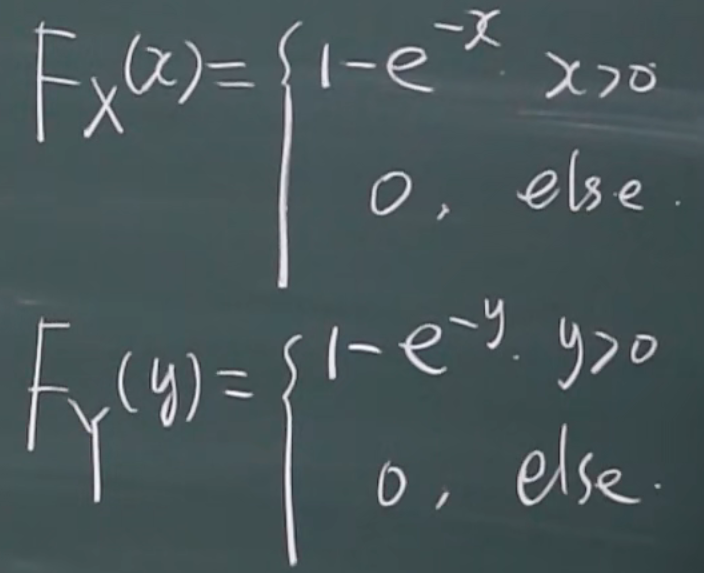
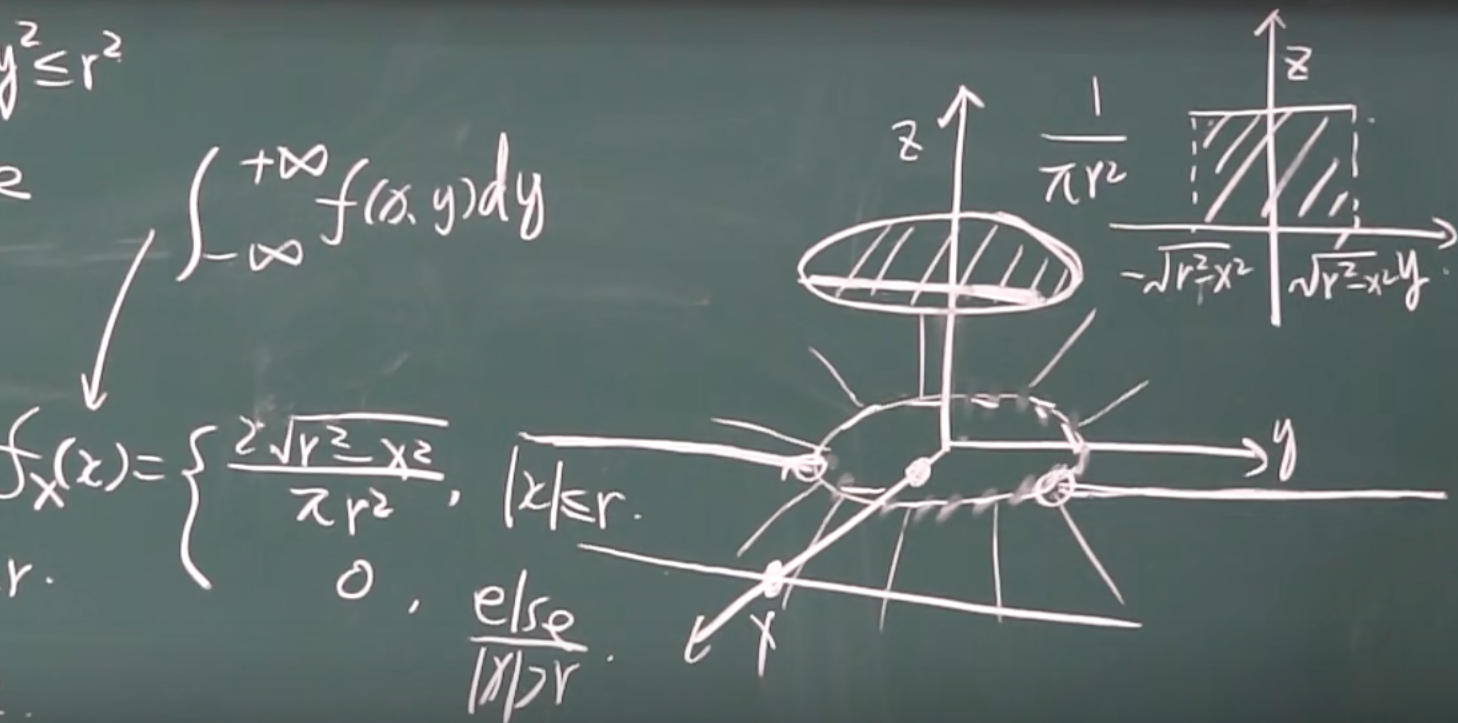
边缘分布函数
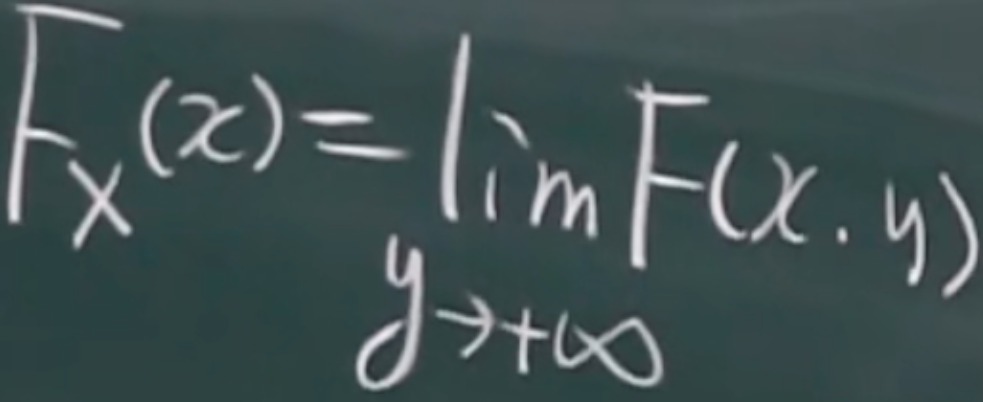
联合密度函数
\(f(x,y)\)
边缘密度函数
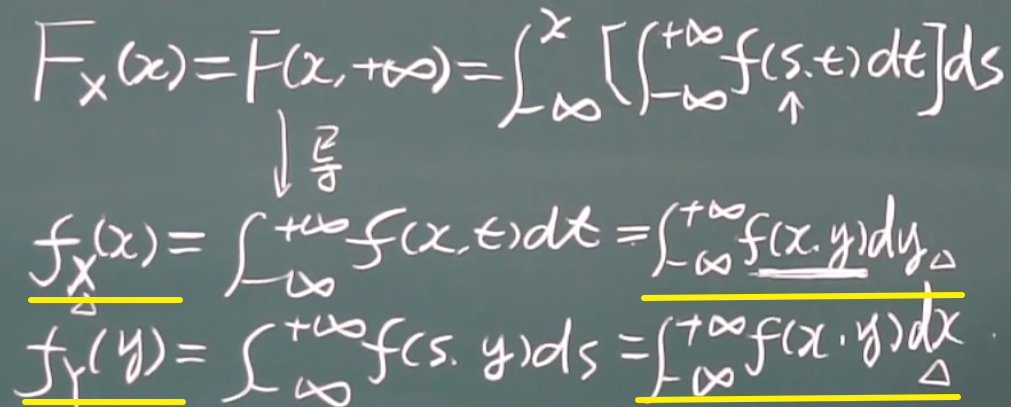
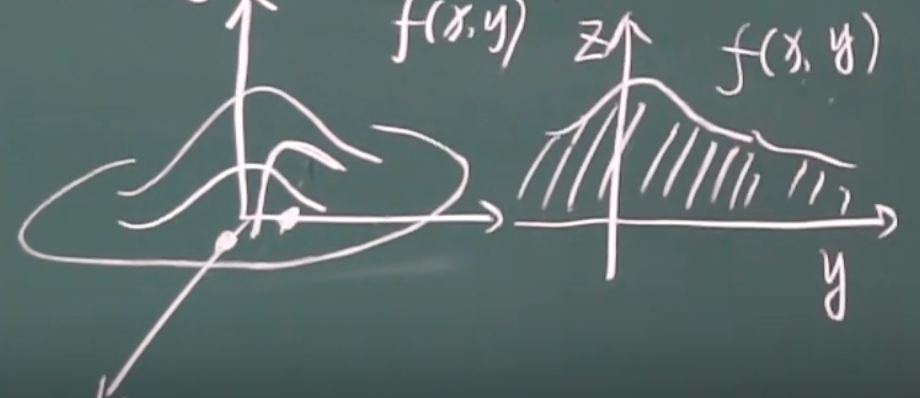
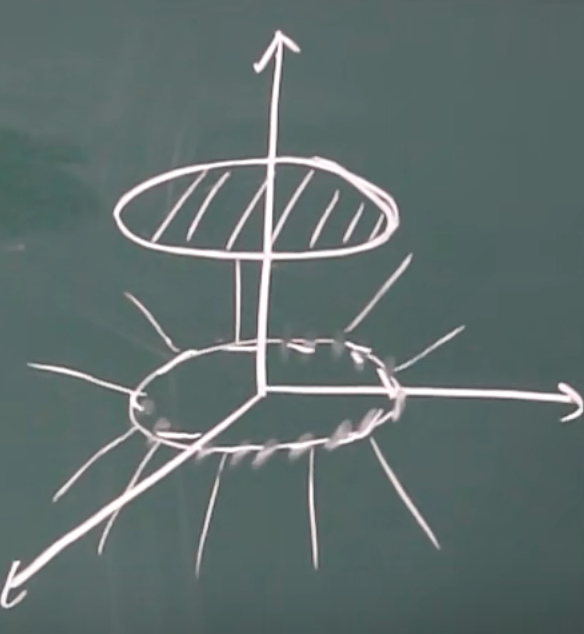
几何含义(以x的边缘密度函数\(f_x(x)\)为例)
x = x0 平面与联合密度函数\(f(x,y)\)相交所得曲线对y积分
( 即整个体积中的一个垂直于x轴的面片,过点 (x0 , 0 , 0) )
补充知识点:
变上限积分
1.上限求导
2.上限带入
例题
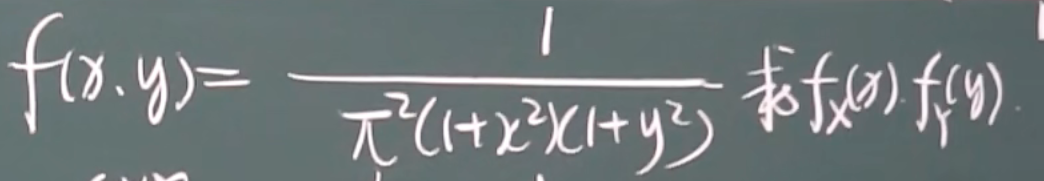
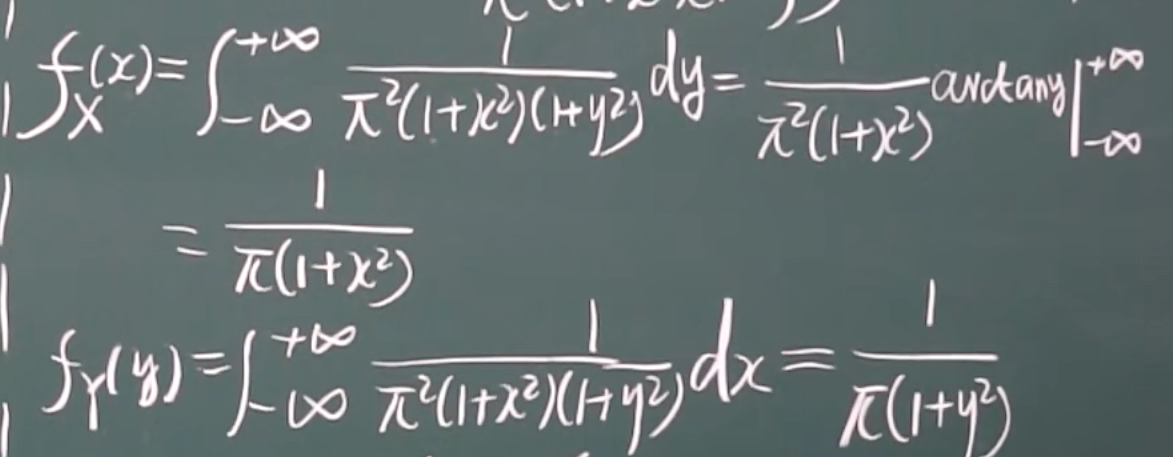
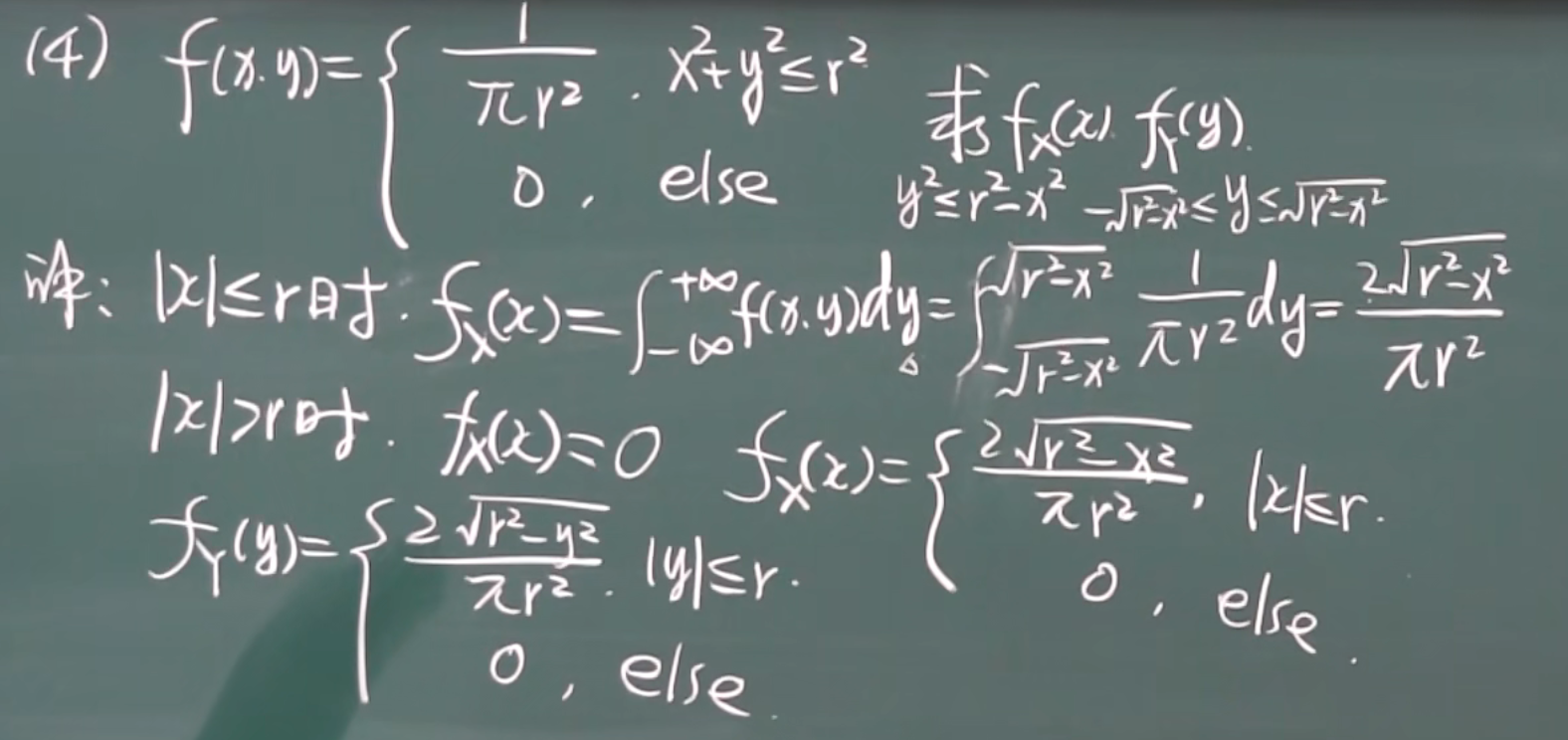
联合密度函数图像
边缘密度函数图像
(以\(f_x(x)\)为例)
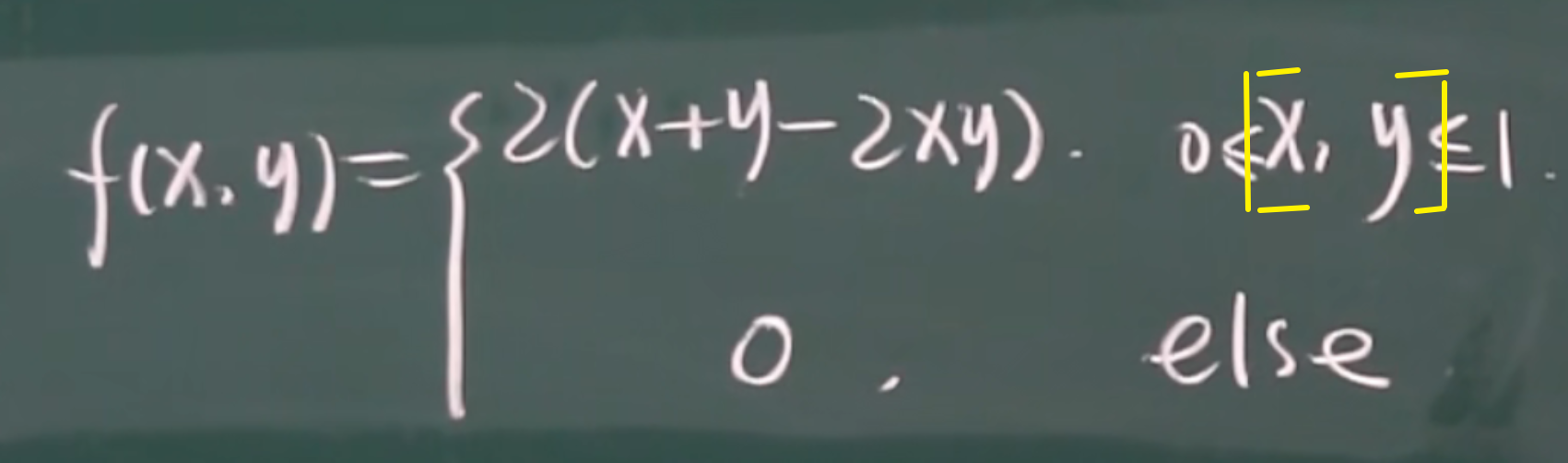
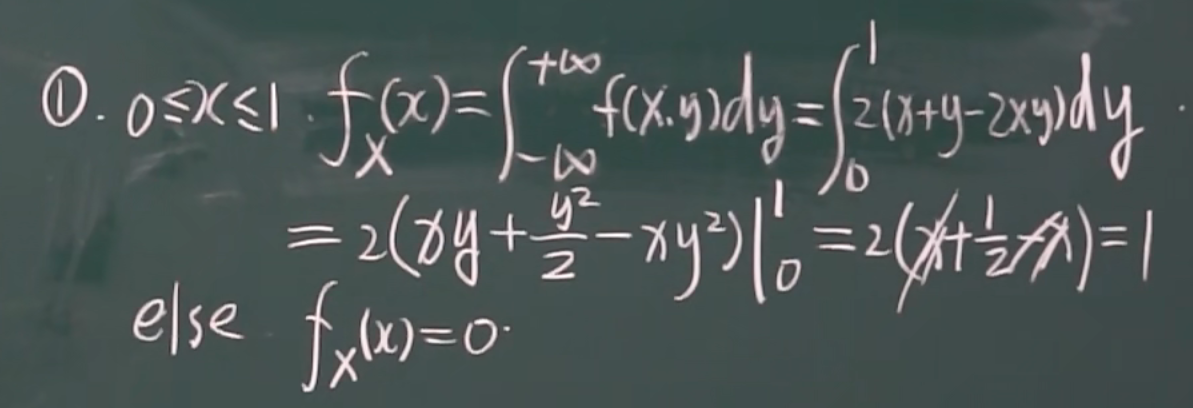
常见二维分布
二维均匀分布
G是有界区域
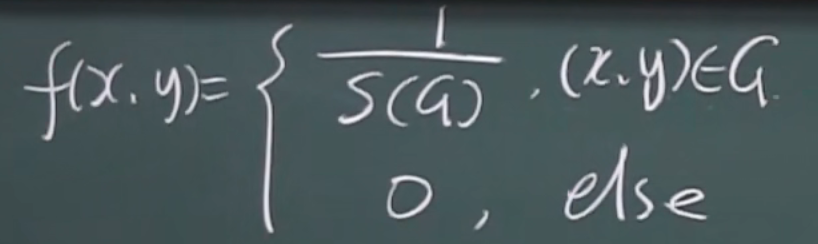
二维正太分布

3.2.1-3.2.3 条件分布(学校不考)
3.2.4 随机变量的独立性
判断条件
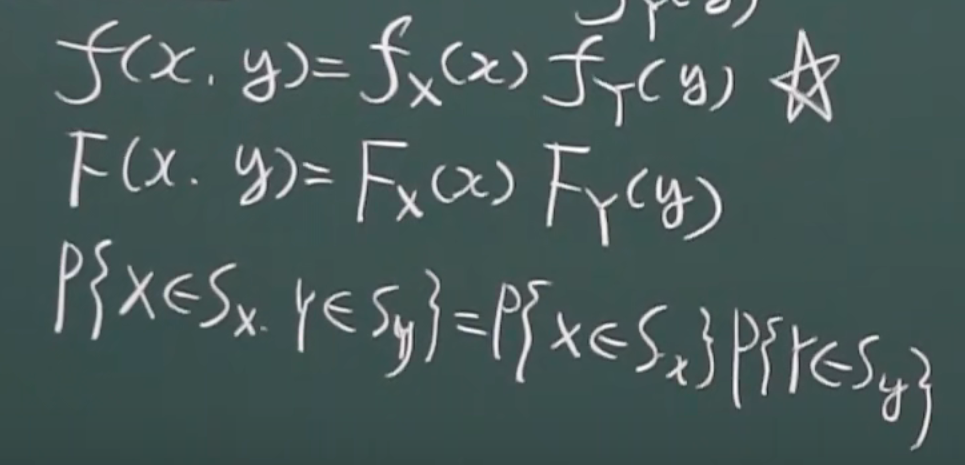
则x,y独立
(优先用第一个判断)
二维离散型的独立性
判断公式
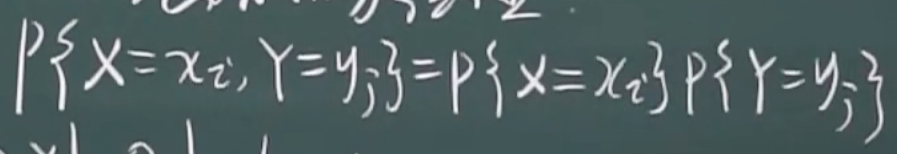
eg
不独立(只要有一个不等则不独立)
0.4*0.4 != 0.2
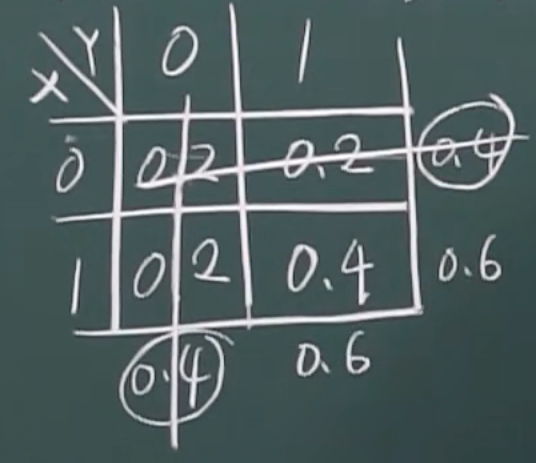
独立(每个都要相等)
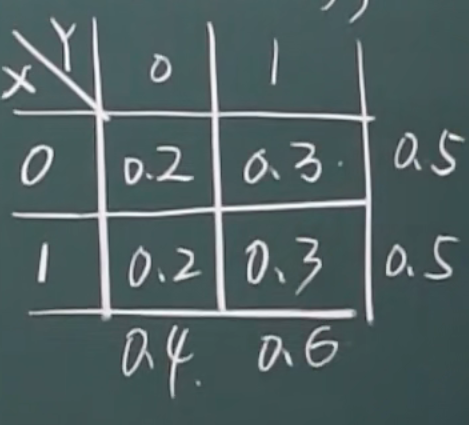
二维连续型的独立性
判断公式
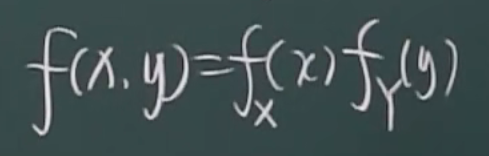
eg

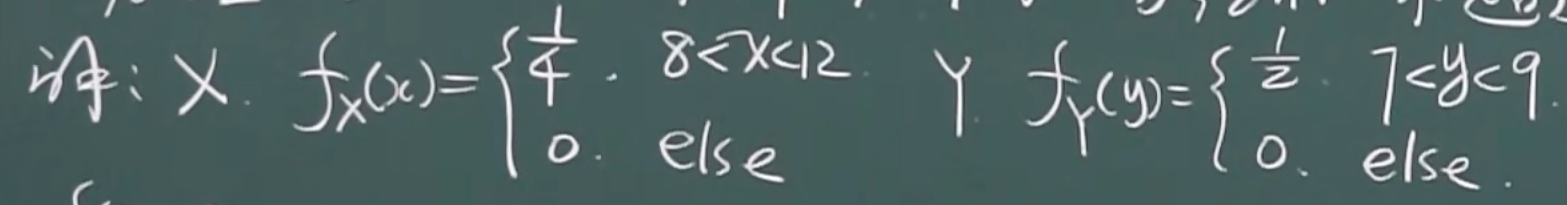
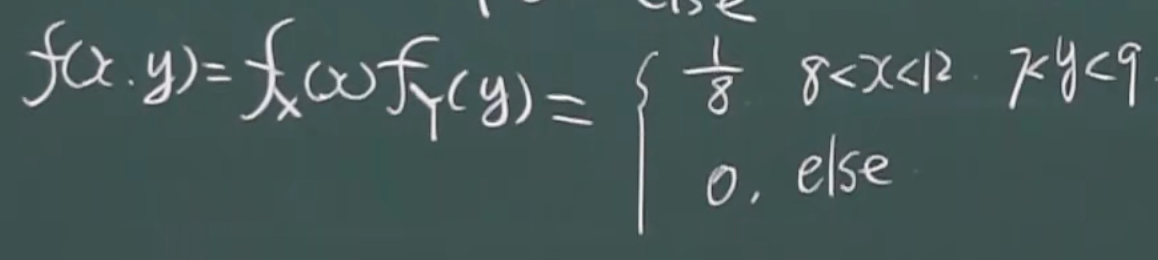
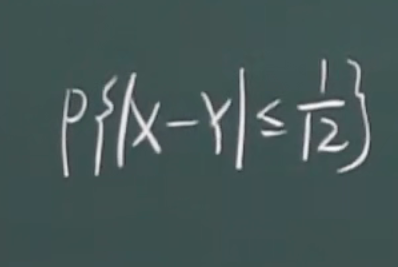
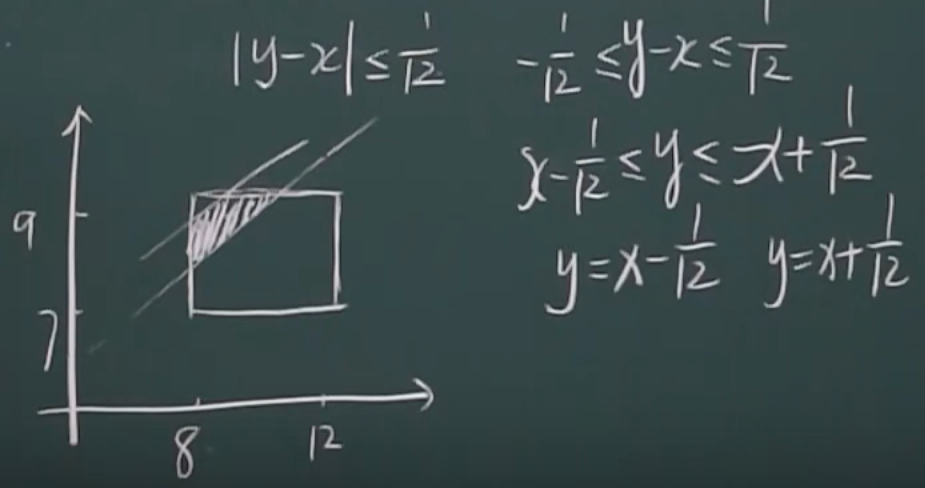
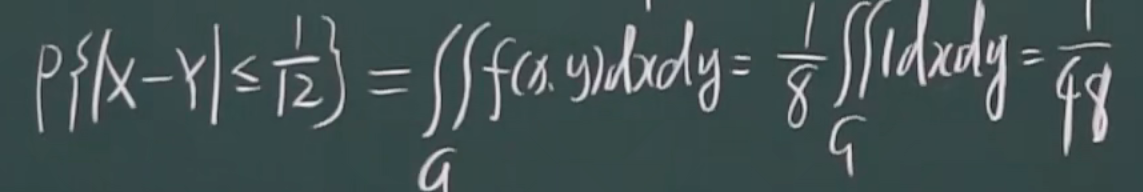
变量独立,构造的函数也独立
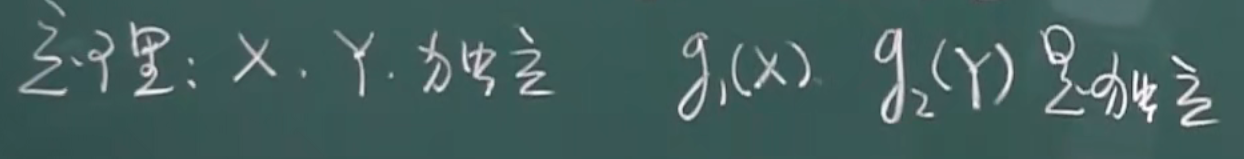
eg
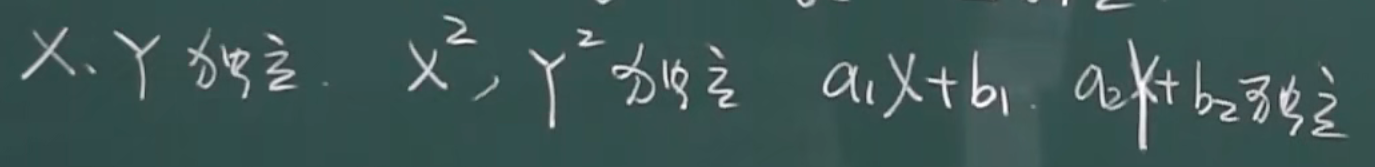
3.3.1 二维离散型随机变量函数的分布
注意:重复的要合并
eg
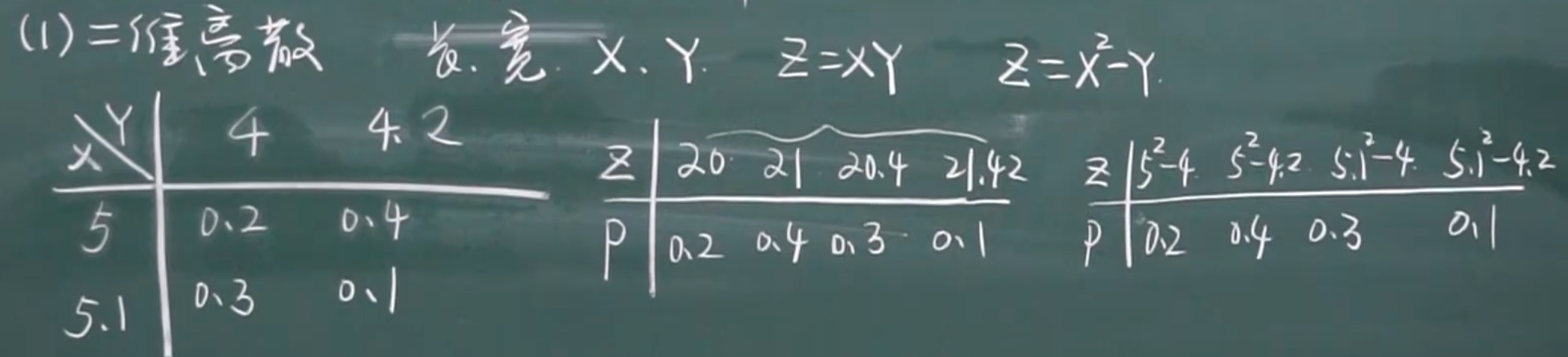
两个0-1分布相加是二项分布
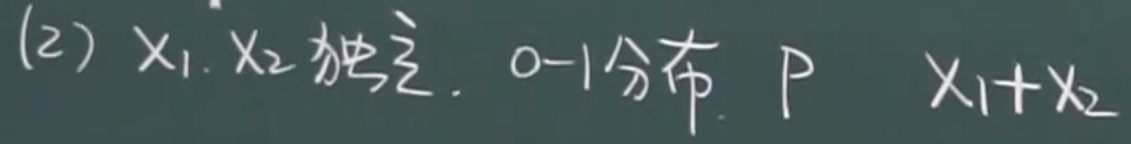
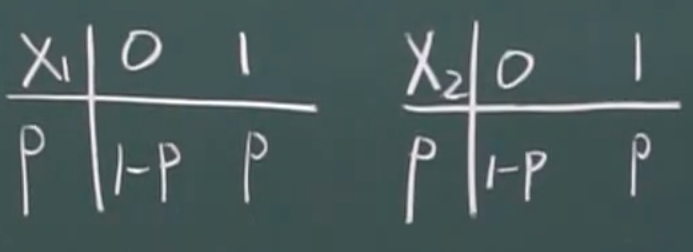
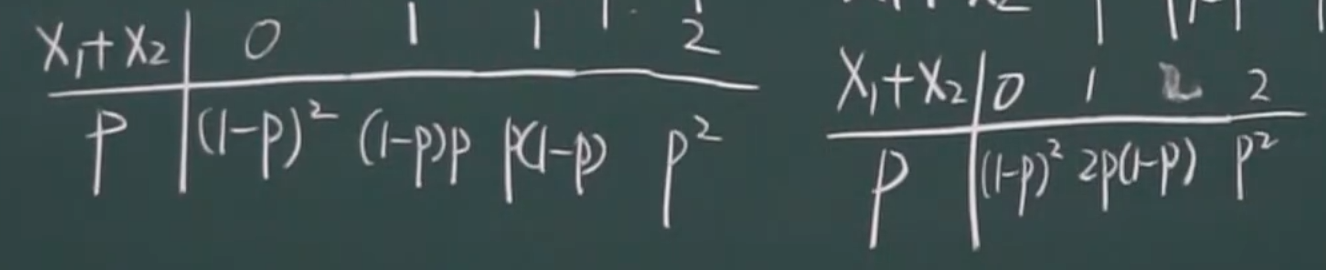
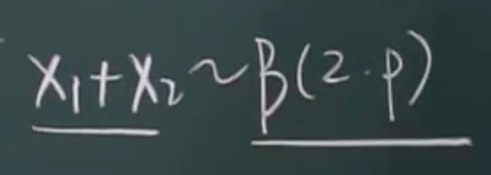
两个泊松分布相加是泊松分布
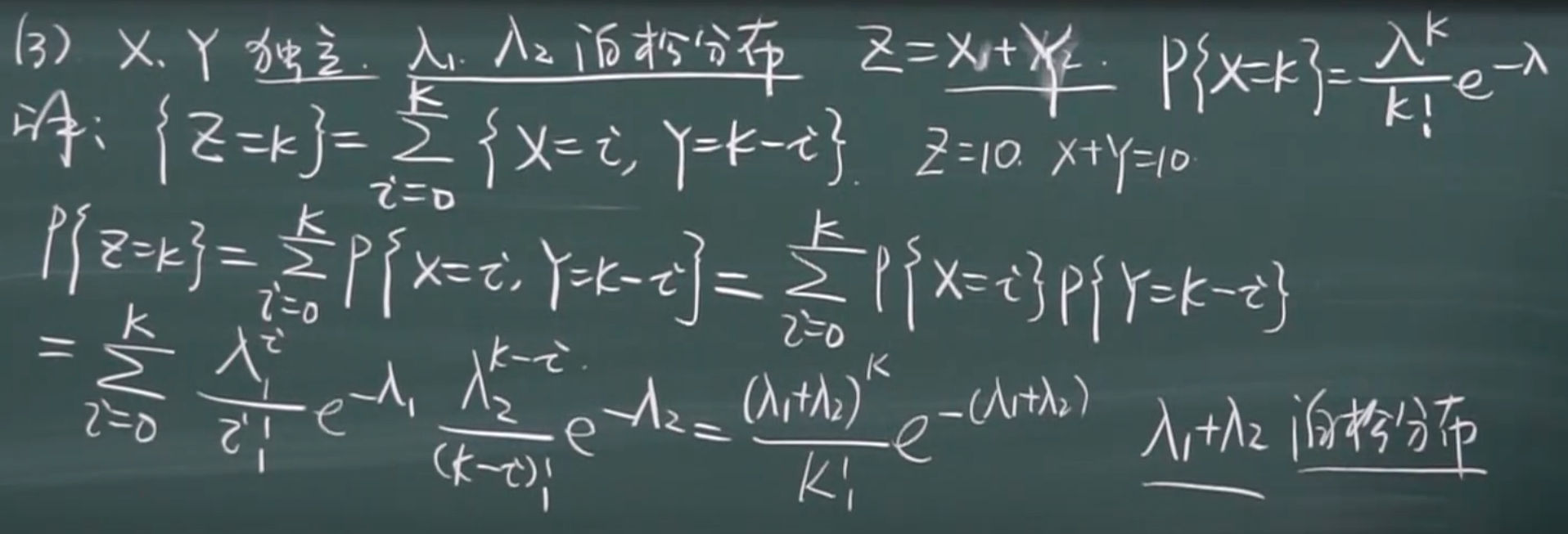
3.3.2二维连续型随机变量函数的分布
《概率论与数理统计》教学视频全集(宋浩)_哔哩哔哩_bilibili
1.先求分布函数
2.对分布函数求导,得密度函数
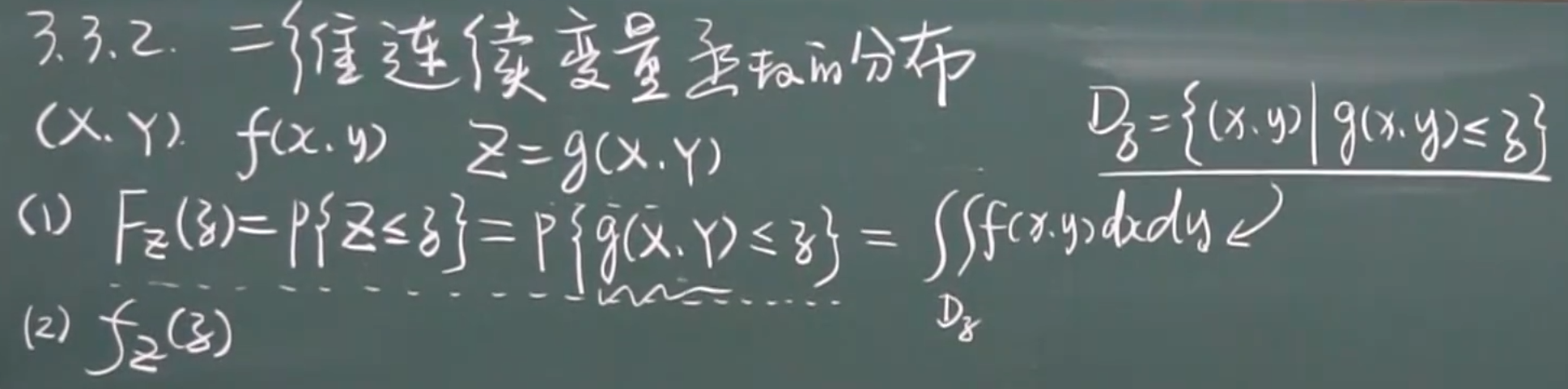
eg
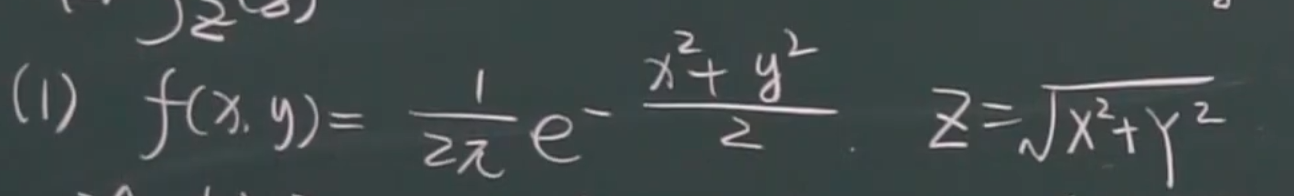
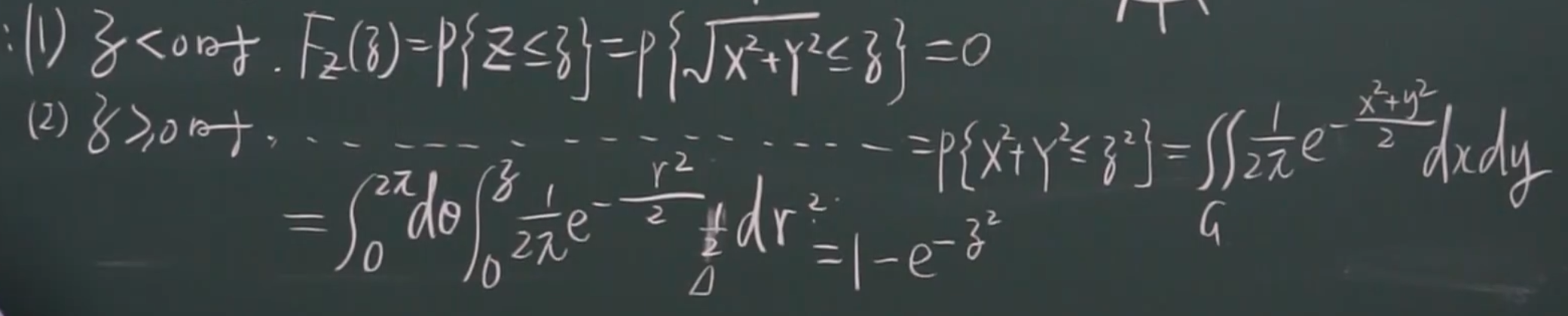
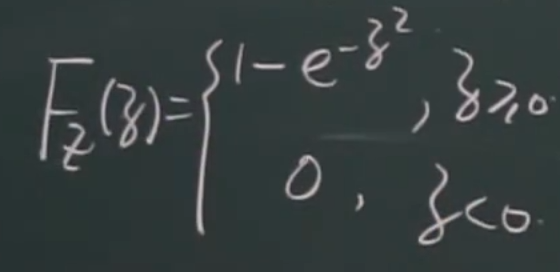
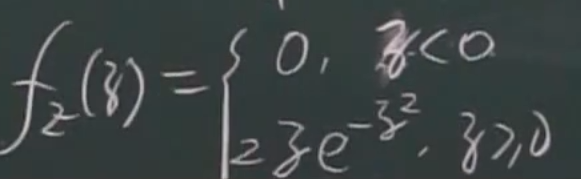
中间步骤(二重积分:极坐标)
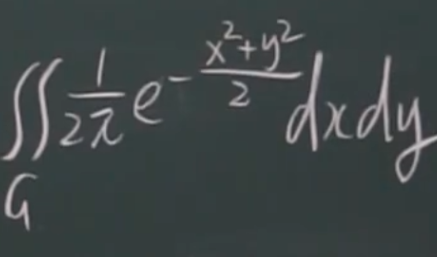
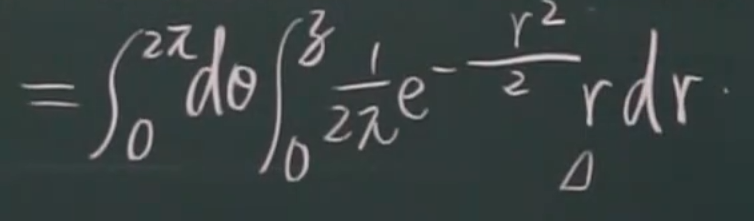
1. Z = X + Y
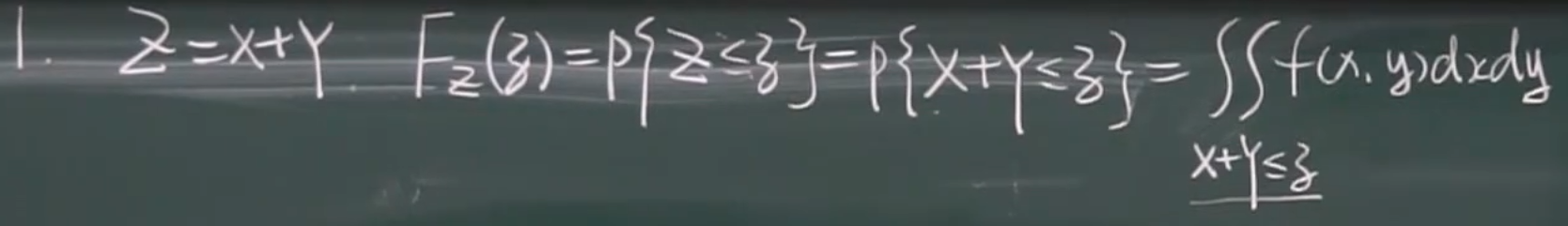


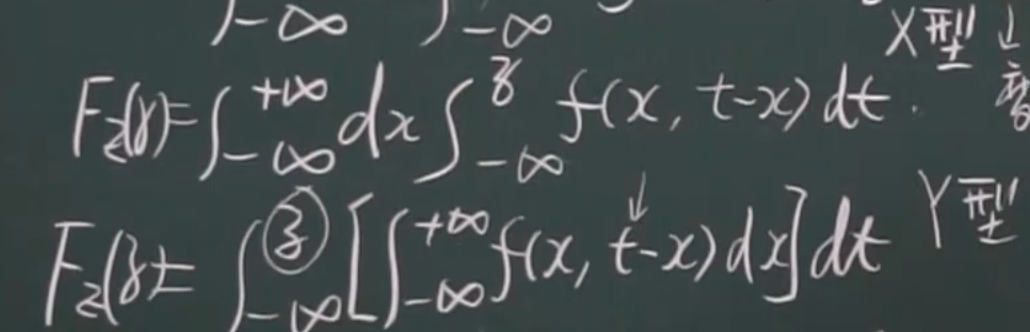
(注1:二重积分的积分区域是长方形时,交换积分次序上下限不变,其他情况要变限)
(注2:Y型更方便求导)
求导得:
卷积公式
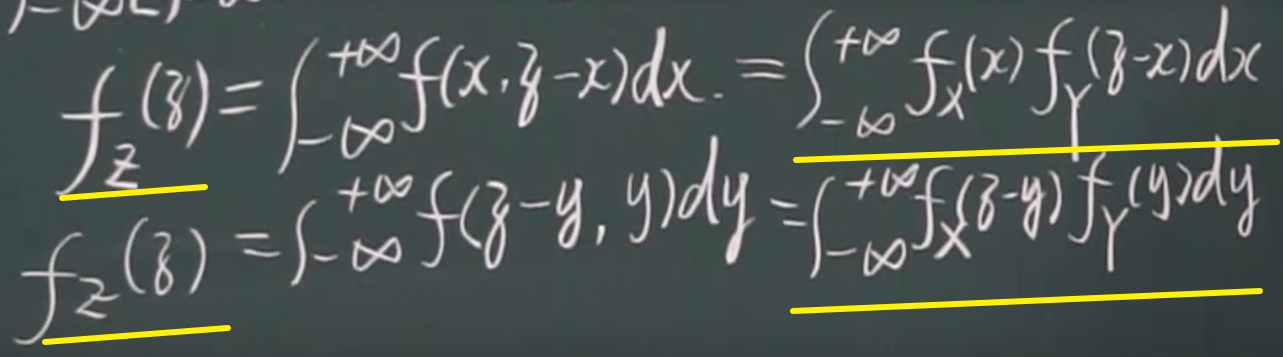
卷积公式使用条件
- Z = X + Y
- X,Y独立
例题
X,Y是标准正太分布
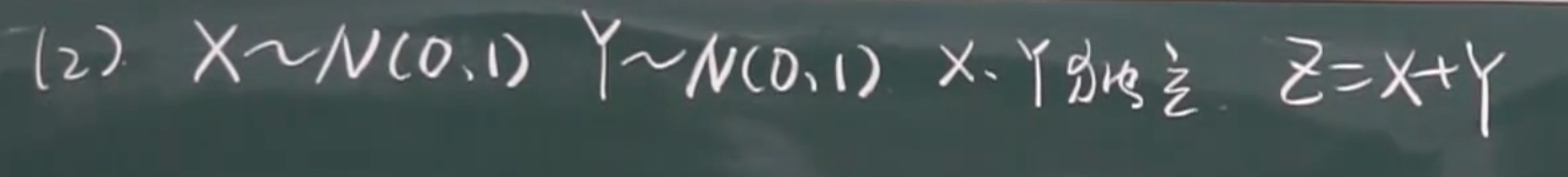
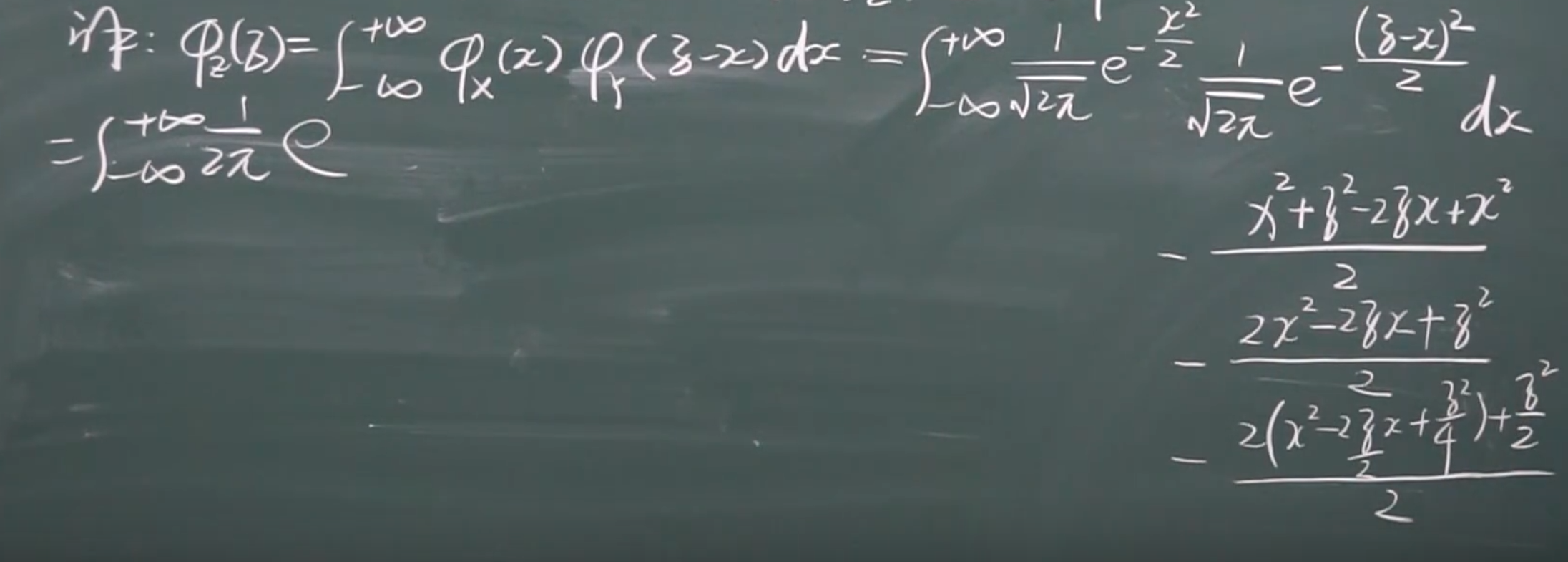
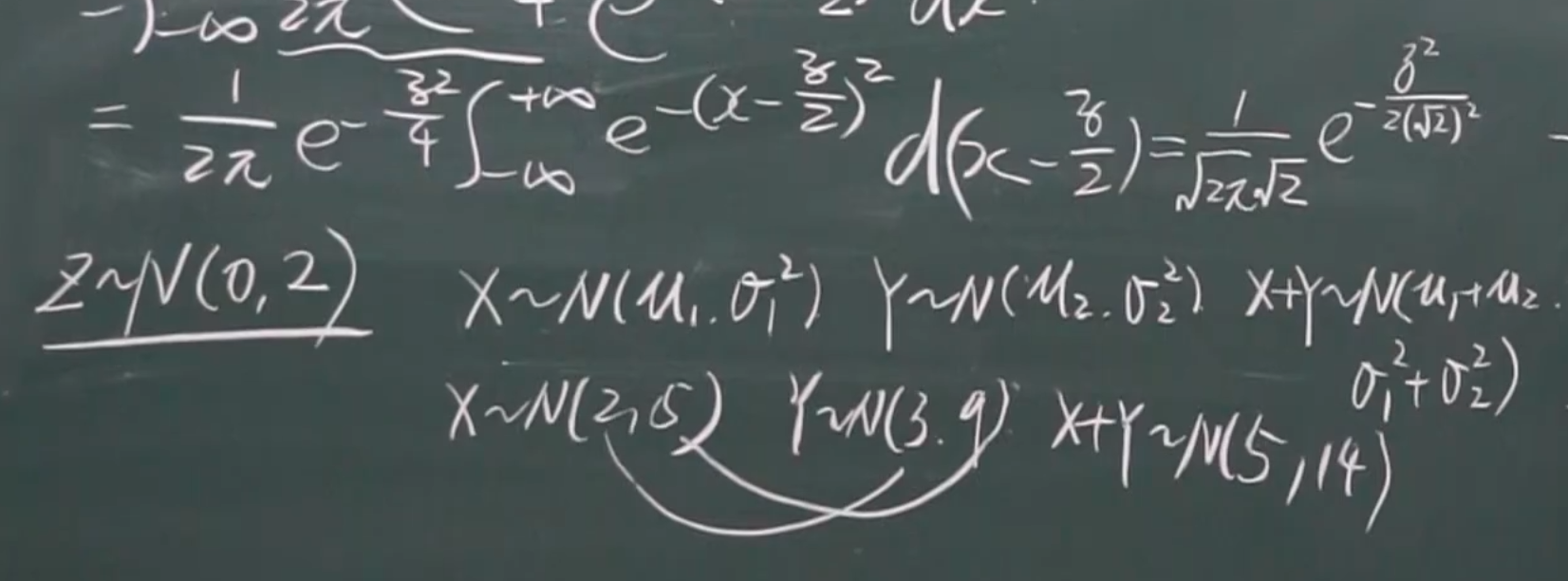
两个正太分布相加是正太分布(有公式)
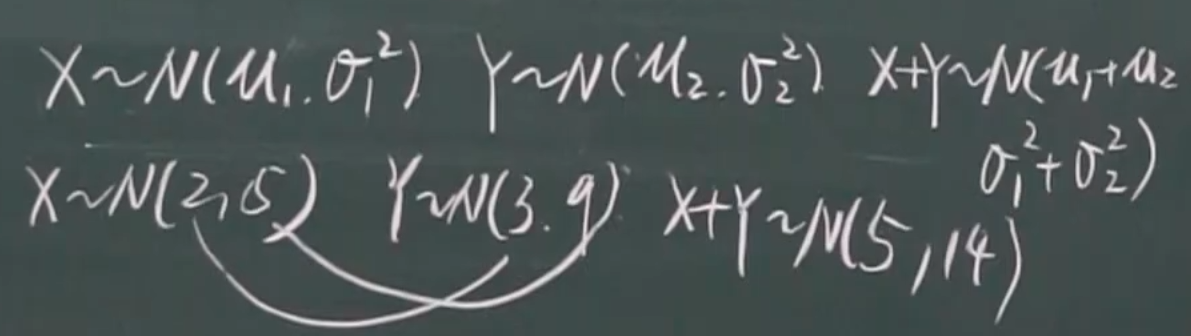
2. M = max{X,Y} & N = min
X,Y独立
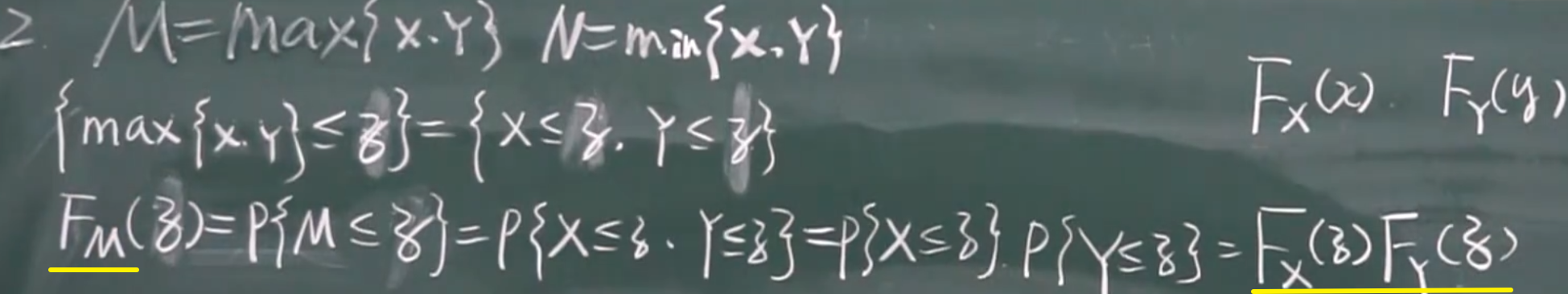
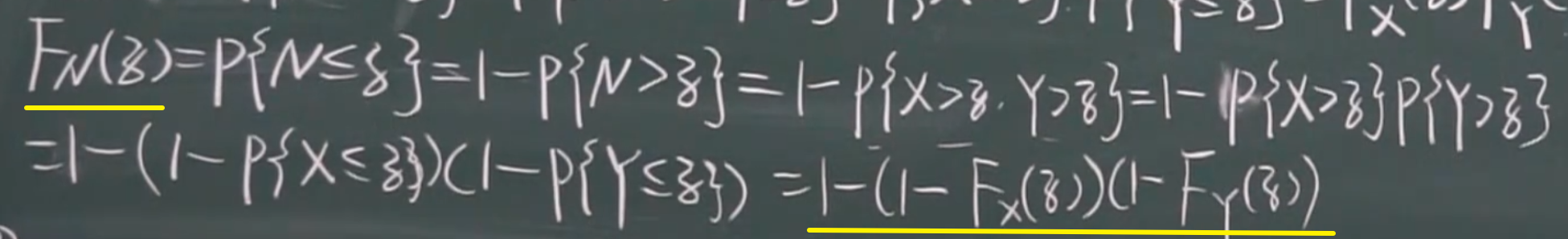
eg
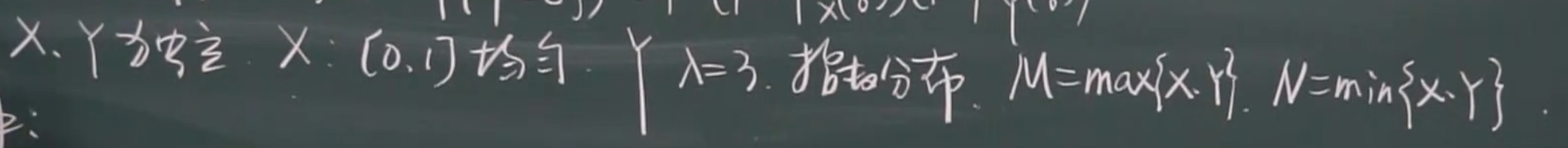
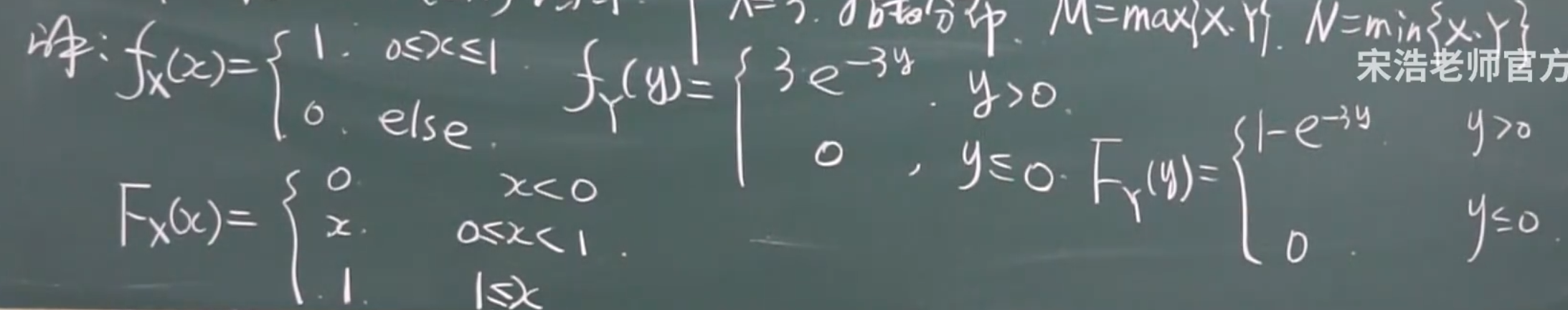
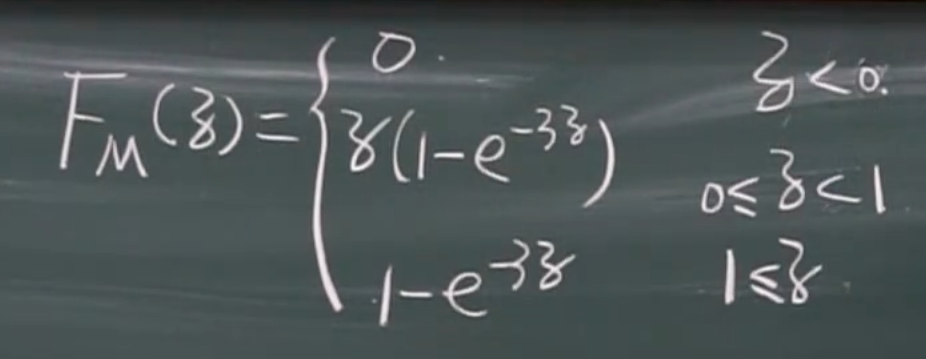
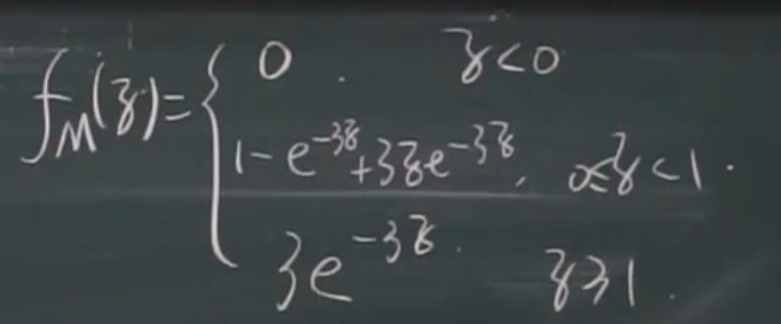
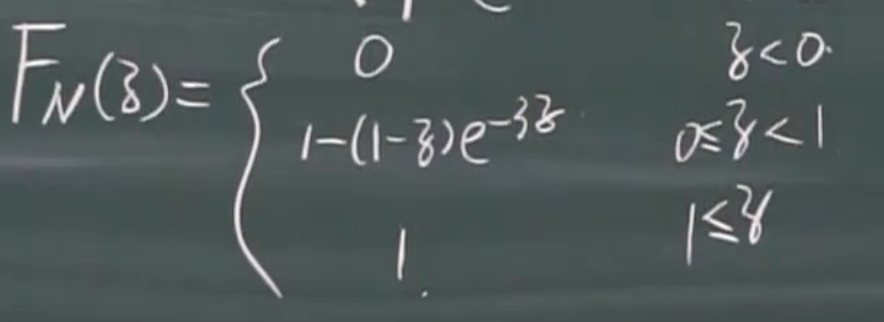
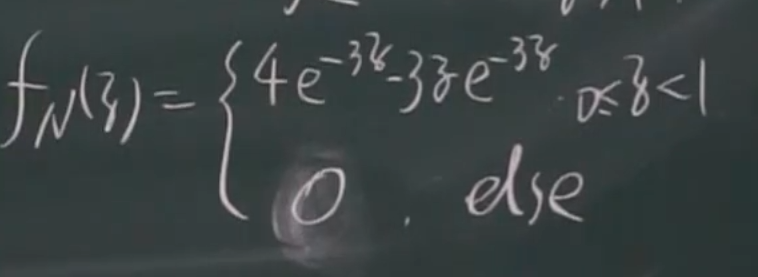

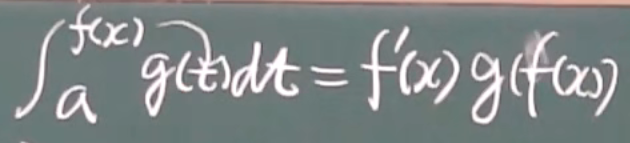

 浙公网安备 33010602011771号
浙公网安备 33010602011771号