第二章：随机变量及其分布

2.1 随机变量的概念

image-20220304110733556

事件的表示

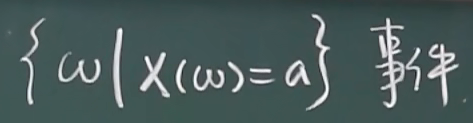
image-20220304111050045

eg：X（硬币反面朝上）= 1

简化

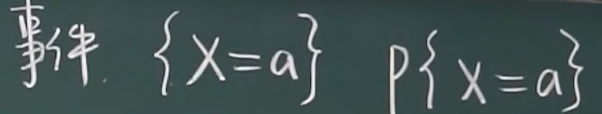
image-20220304111102973

eg：X = 1 代表硬币反面朝上这个事件

image-20220304111842139

2.2.1 离散型随机变量及其概率分布

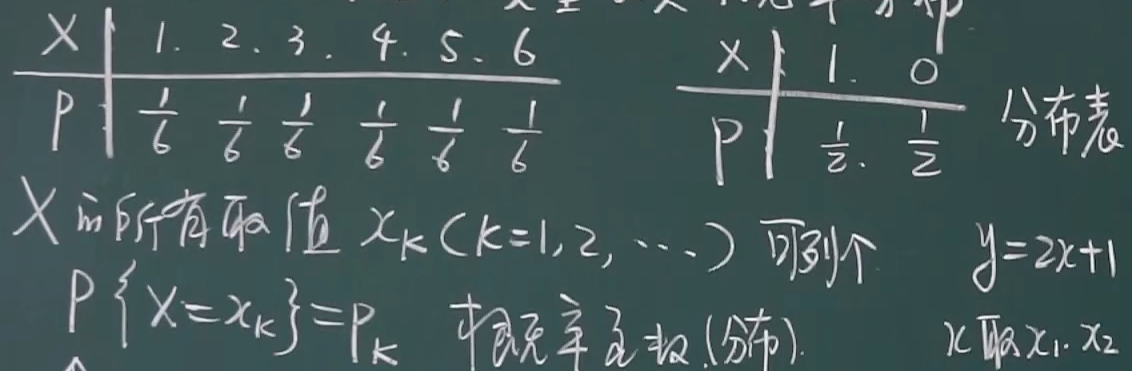
image-20220308143511041

概率图

image-20220308143531441

例题

image-20220308144010109

image-20220308144044097

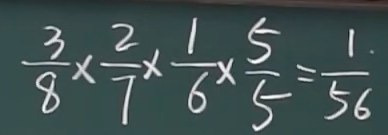
image-20220308144115732

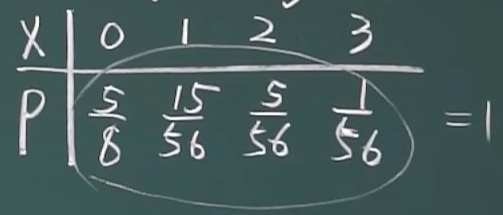
image-20220308144240806

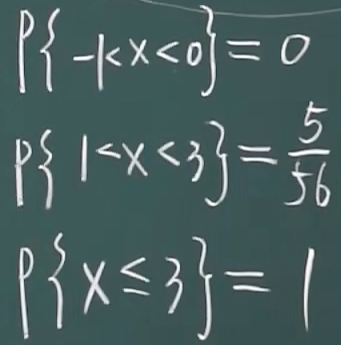
image-20220308144419644

2.2.2 连续性随机变量及其概率密度函数

引例

image-20220308145042199

频数直方图

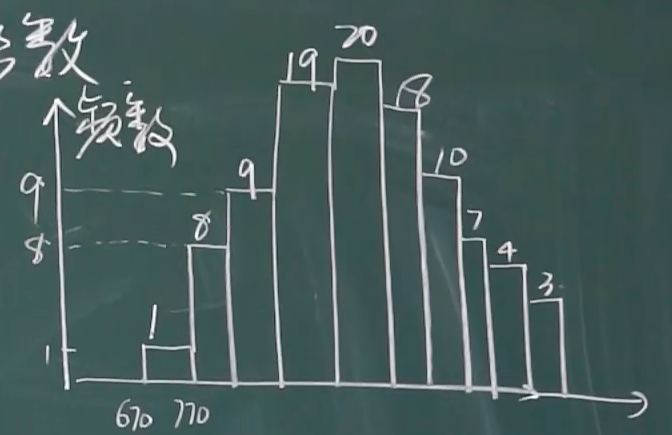
image-20220308145157277

频率密度直方图

image-20220308145449651

性质

image-20220308150004096

当组距趋近于无穷小时：

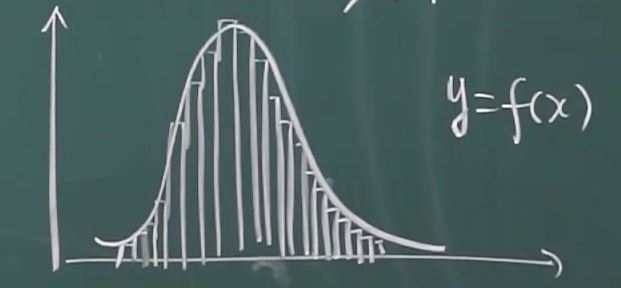
image-20220308150111701

概率分布密度函数

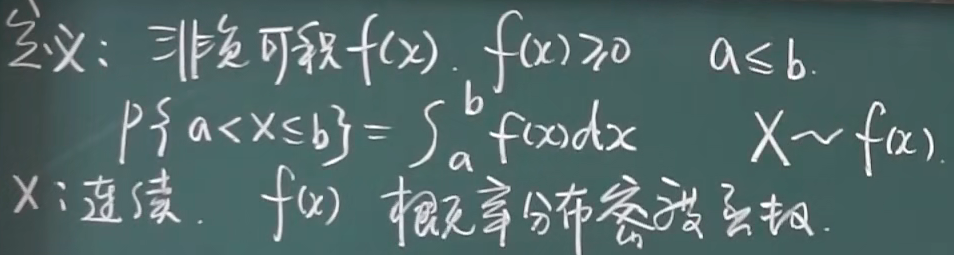
image-20220308150259155

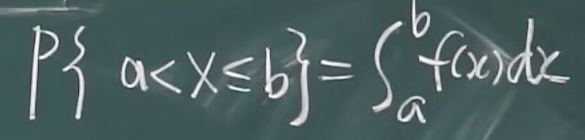
image-20220308152714967

性质

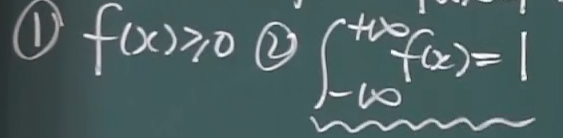
image-20220308150458777

图像上点的含义

f(x1)表示X取x1附近值时概率的大小

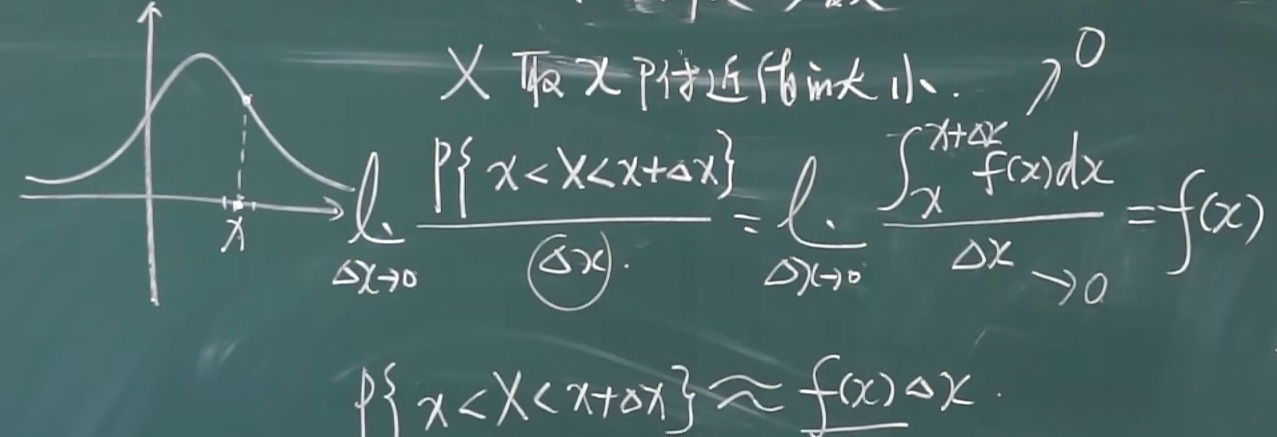
image-20220308155120738

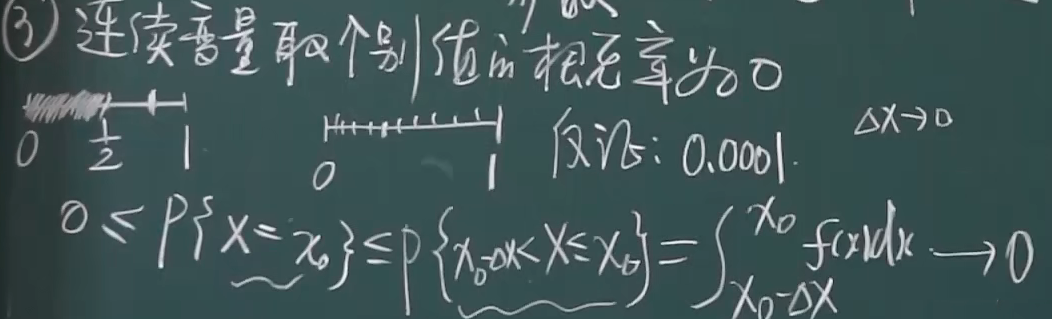
image-20220308151601884

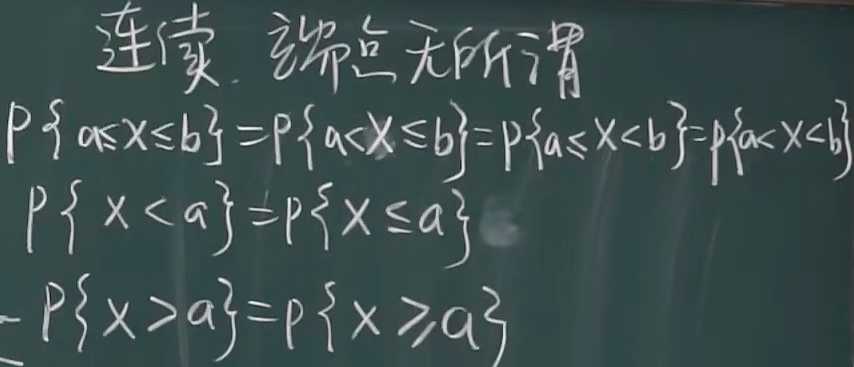
image-20220308151803739

image-20220308152243164

例题

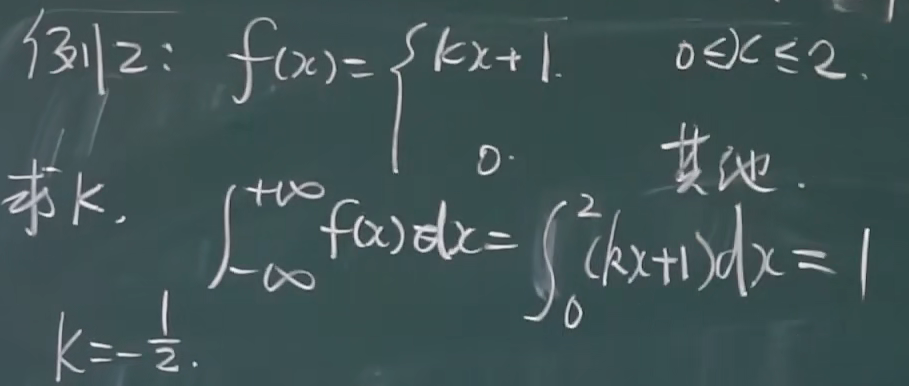
image-20220308152617548

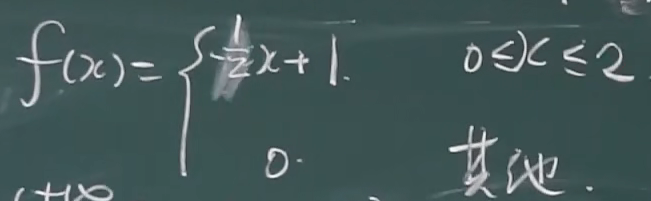
image-20220308152900354

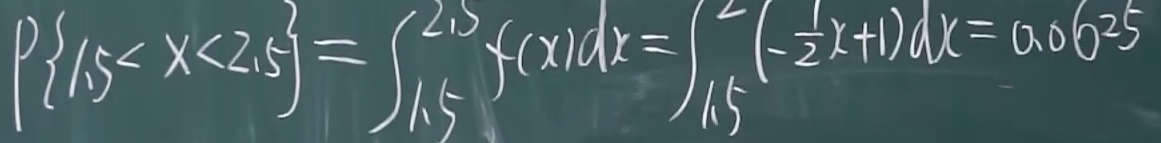
image-20220308152947167

2.2.2 分布函数的定义

定义

image-20220308192224865

小写的x是实数，大写的X是随机变量，{X<=x}表示事件

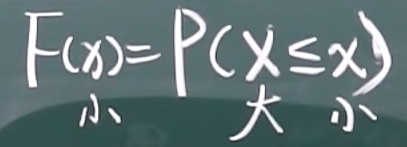
image-20220308200327006

性质

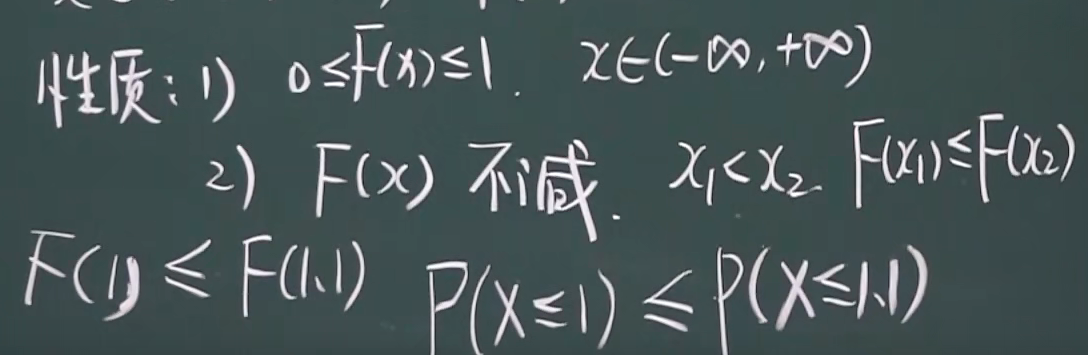
image-20220308192245173

image-20220308192510955

image-20220308192550774

image-20220308192556315

观察离散型分布函数图像：从左边逼近函数值不等于极限值，从右边逼近函数值等于极限值

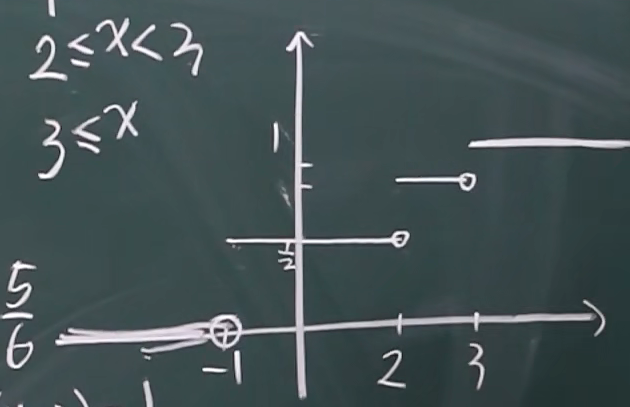
image-20220308201040517

右连续

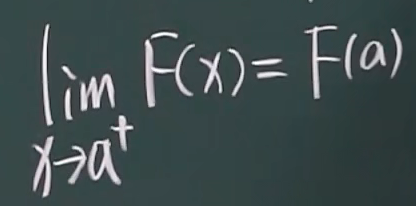
image-20220308193101402

左连续

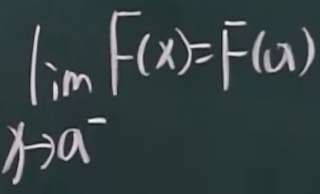
image-20220308193133721

公式-对离散型和连续性都成立

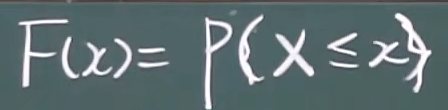
image-20220308194021284

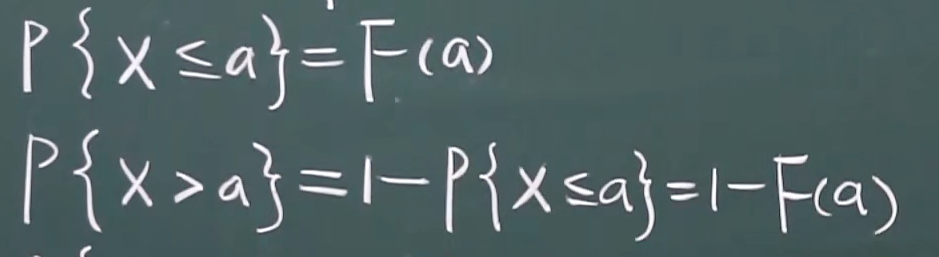
image-20220308194035497

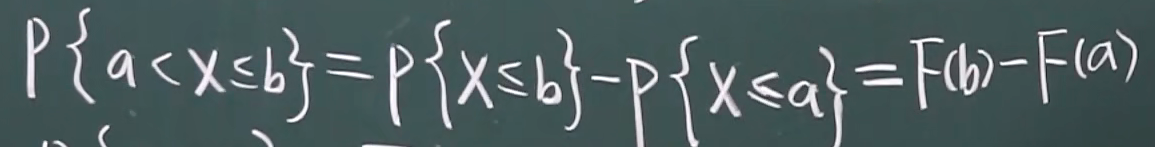
image-20220308194051846

F(a-0)是函数在a点的左极限，F(a-0)=P{X<a},F(a)=P{X<=a}

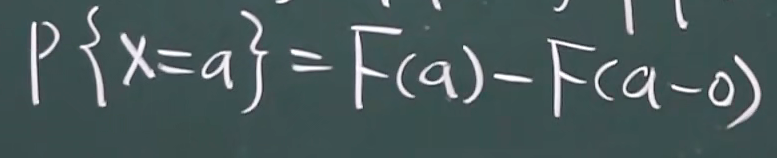
image-20220308194102124

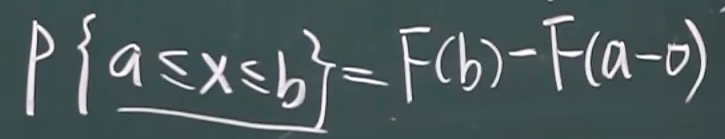
image-20220308194449089

从左边无限接近a但不包含a

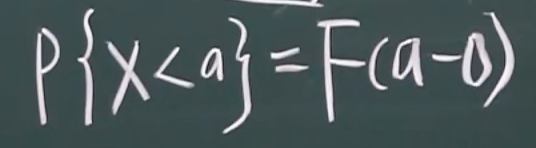
image-20220308194643477

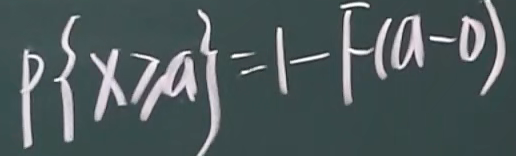
image-20220308194746017

2.2.2 离散型的分布函数

例题

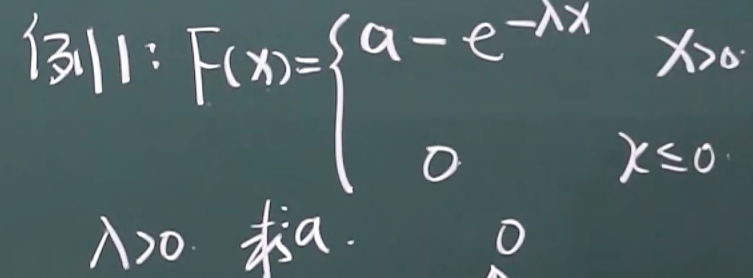
image-20220308195839386

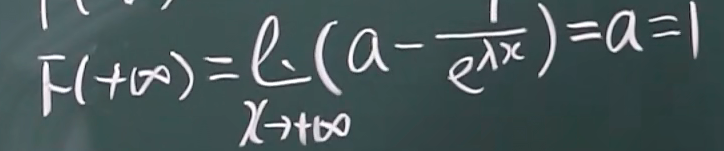
image-20220308195851761

2.重点：根据分布表求离散型的分布函数

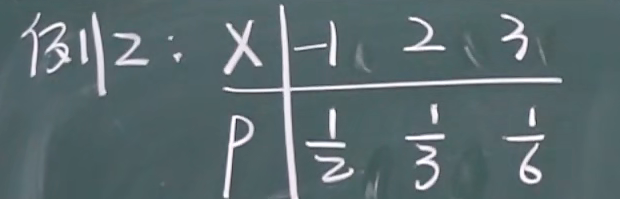
image-20220308200910906

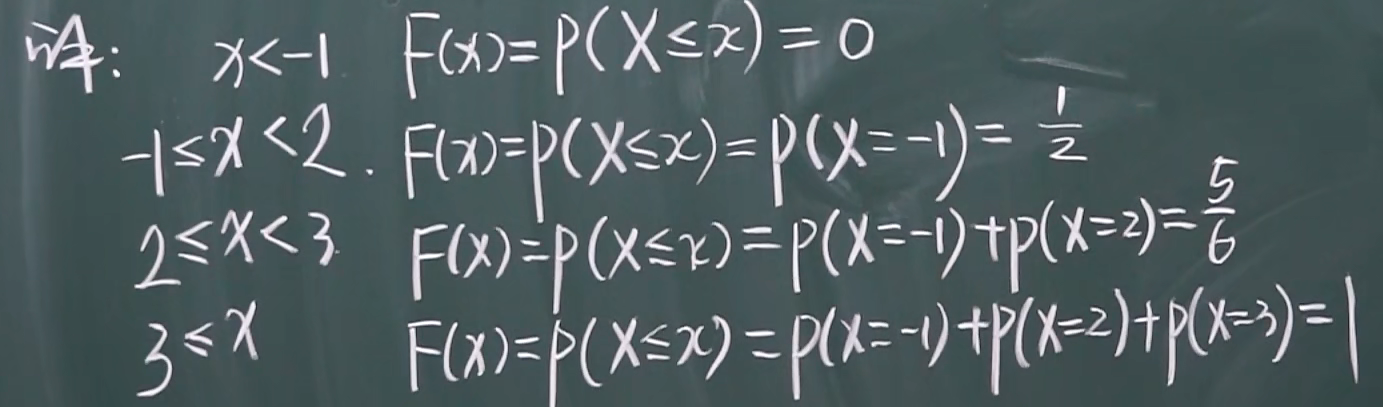
image-20220308200917493

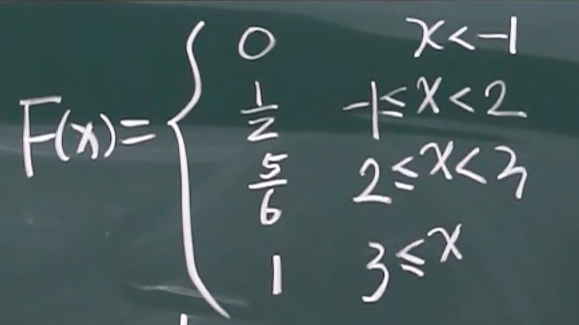
image-20220308200950429

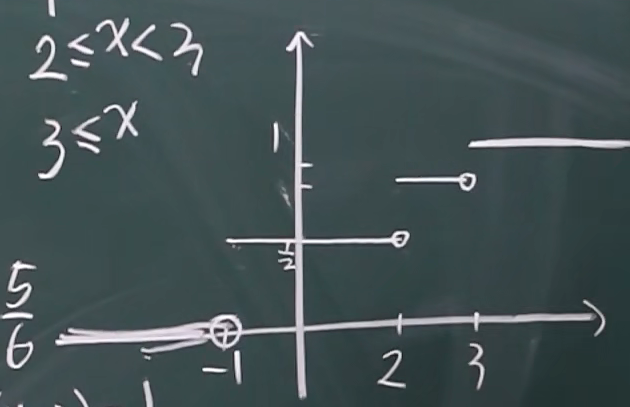
image-20220308201040517

套路

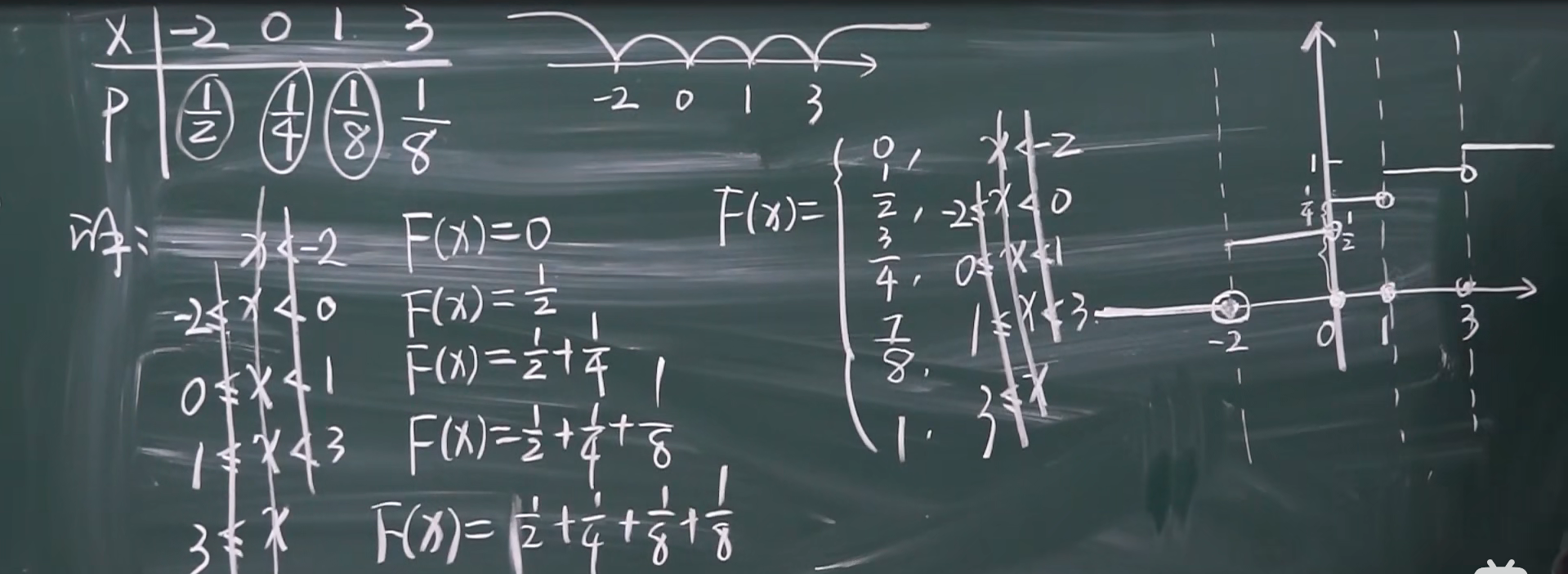
image-20220308202307451

由分布函数求概率函数

分布函数的间断点就是随机变量 X 的取值

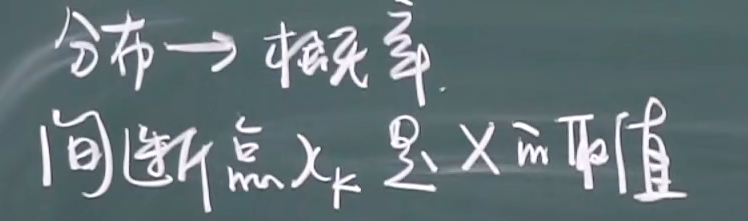
image-20220308203255591

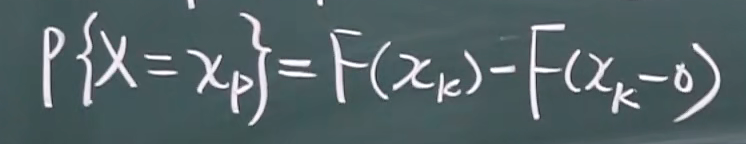
image-20220308203742900

eg:

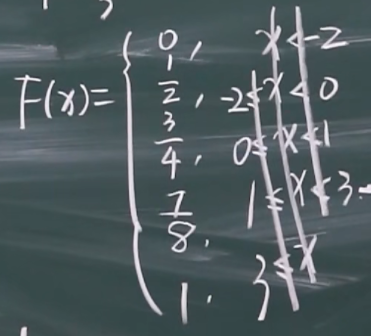
image-20220308203944497

P{X=-2}=F(-2)-F(-2-0)=1/2-0

P{X=0}=F(0)-F(0-0)=3/4-1/2

通常通过观察分布函数的图像求值

2.2.2 连续型的分布函数

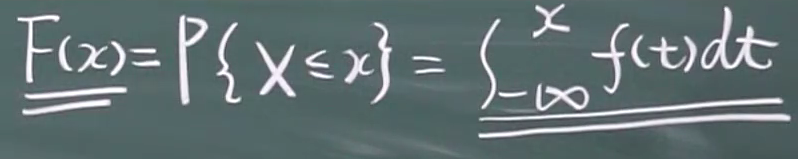
image-20220308211204292

例题：
1.

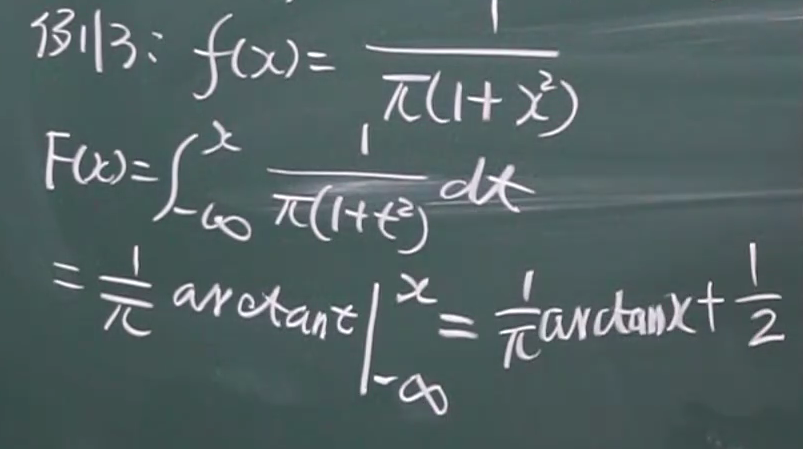
image-20220308211529253

2.由连续型概率密度函数求分布函数

image-20220308212109121

对连续型分布函数求导 = 连续型概率密度函数

3.已知连续型分布函数

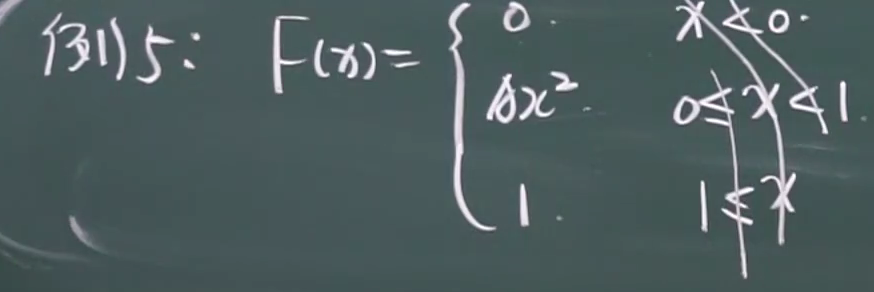
image-20220308212514136

（1）求A

（用此法求不出）

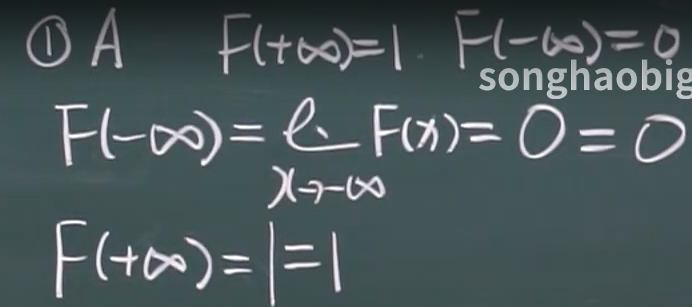
image-20220308212530831

（根据F(x)是连续的，在x=0处用右连续的条件，求不出A）

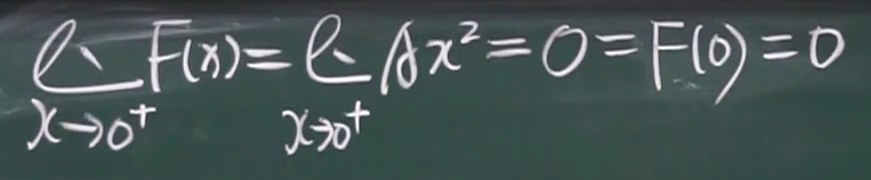
image-20220308212918178

（在x=1处用左连续的条件：左极限等于函数值）为什么用左连续：1左边的函数表达式是Ax平方，与要求的相关

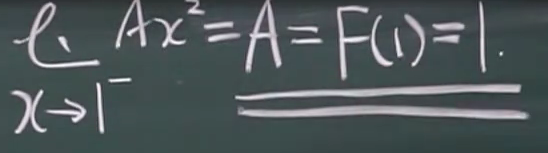
image-20220308213410708

（2）求连续型概率密度函数

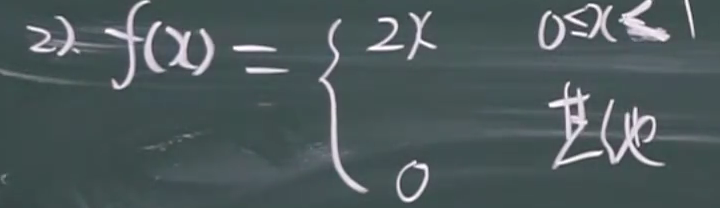
image-20220308213802659

（3）

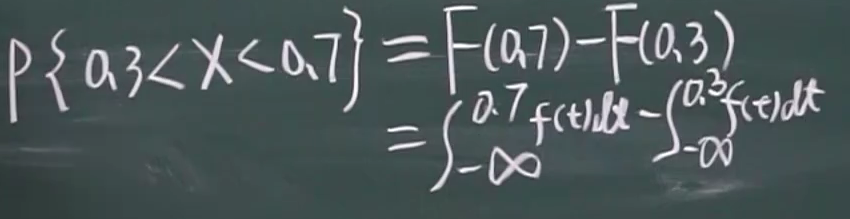
image-20220308213936811

2.2.3 常见随机变量的分布

1.离散型的分布

0-1分布

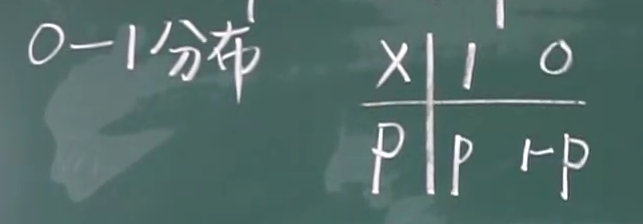
image-20220309202032933

image-20220309202358069

0-1分布是特殊的二项分布，只做一次实验要么发生要么不发生

几何分布

image-20220309202919834

例题

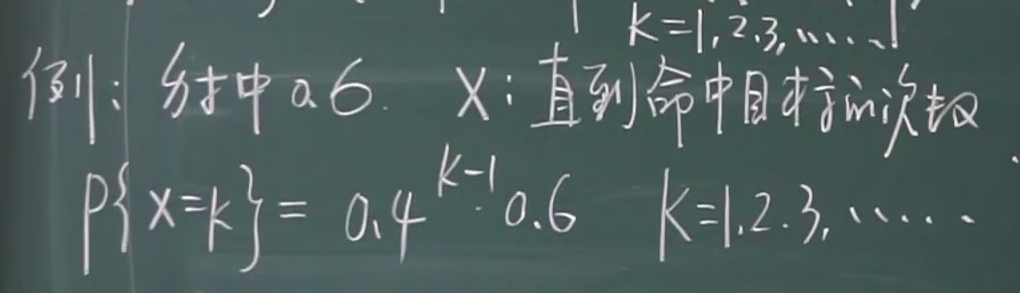
image-20220309203055535

二项分布

image-20220309203401774

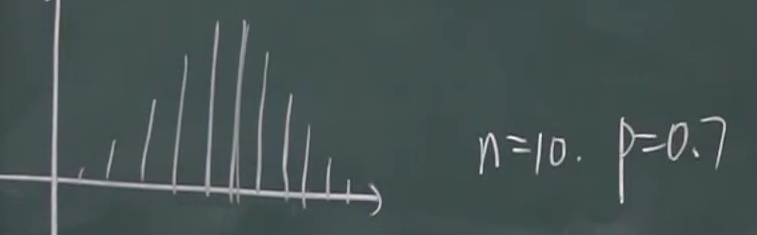
image-20220309203832437

k取何值时P{X=k}最大？

img

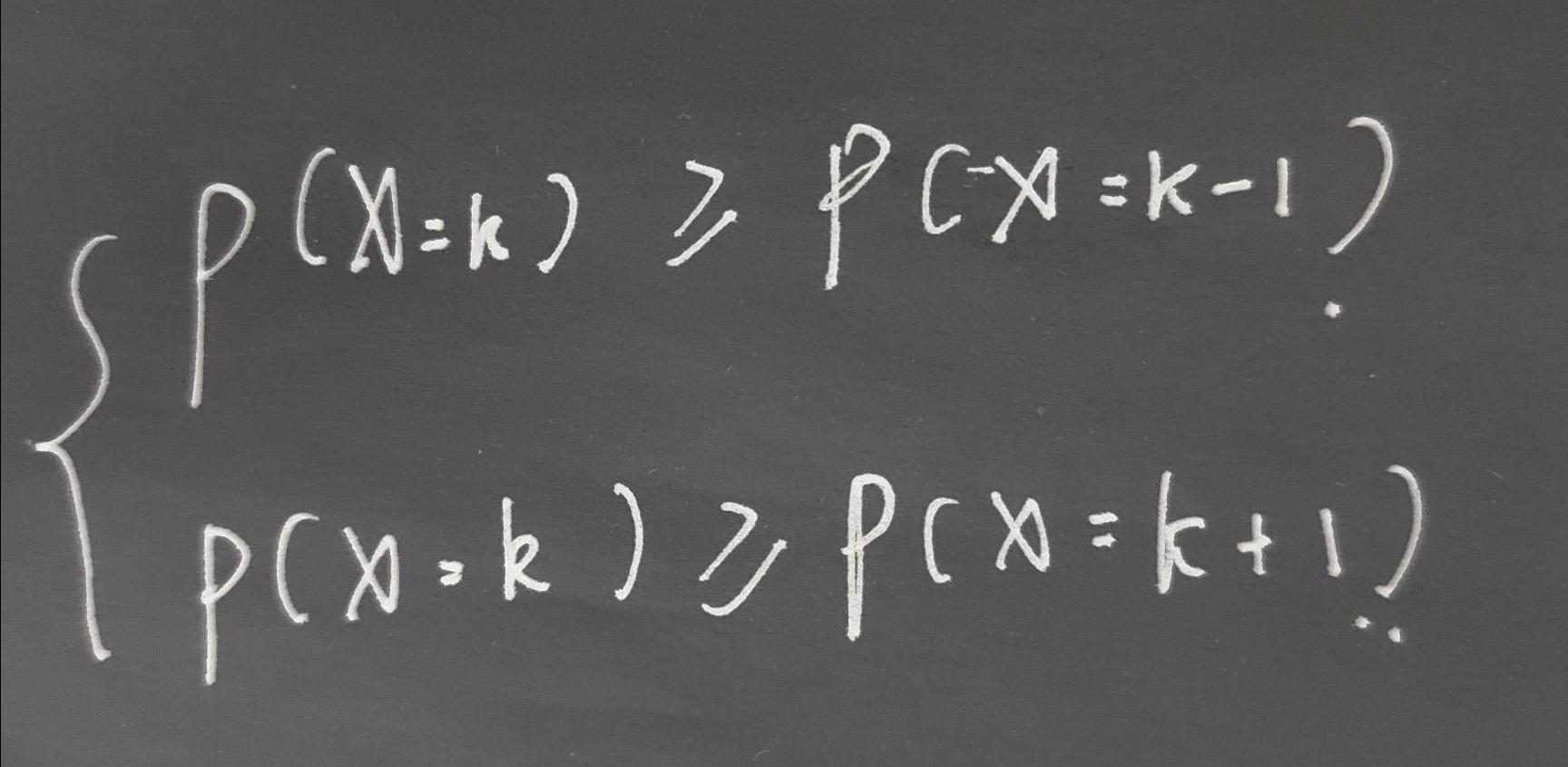
结论：

image-20220309205658504

先计算判断（n+1）p是不是整数

例题：

1.求至少需要安装多少台报警器，n=报警器台数

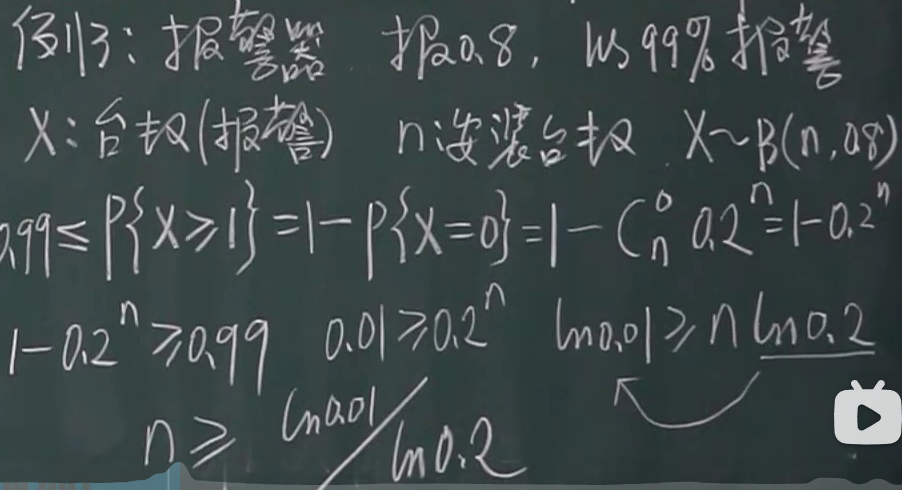
image-20220309210256681

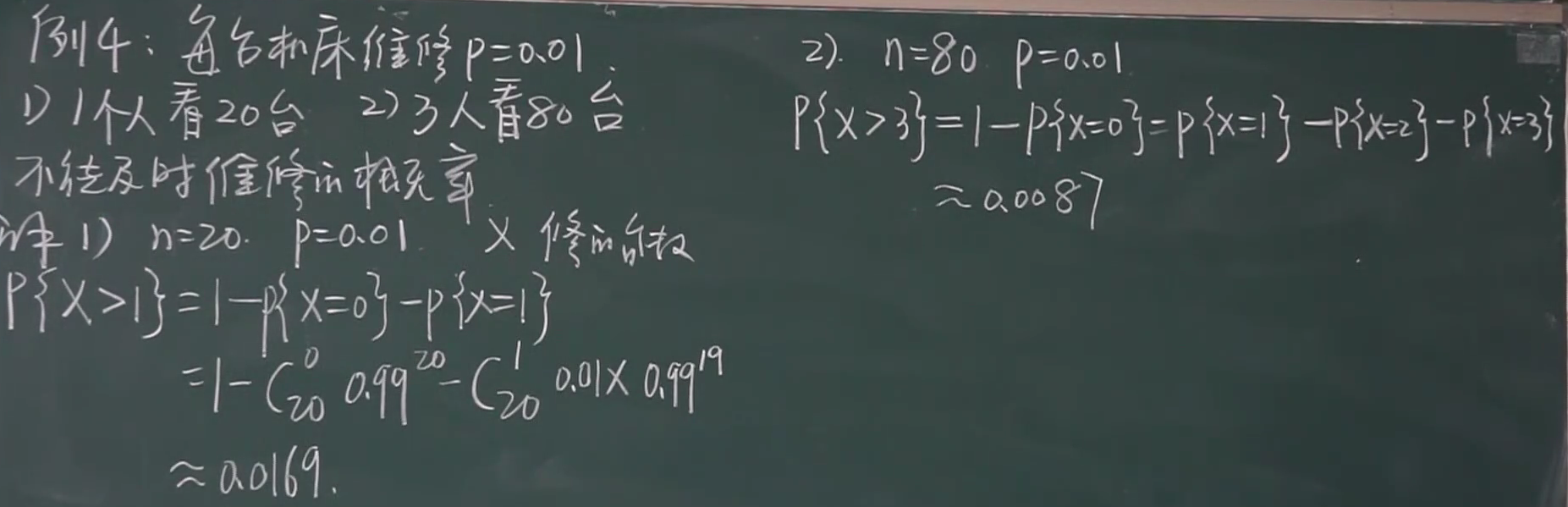
image-20220309210858287

泊松分布

公式

image-20220309211314612

常见题目背景

image-20220309211526651

如何计算

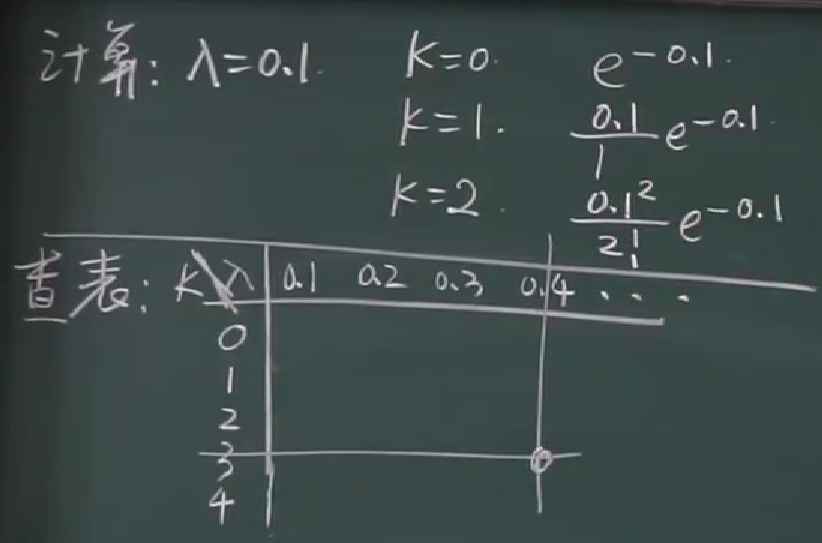
image-20220309211807933

注意另一种分布表

img

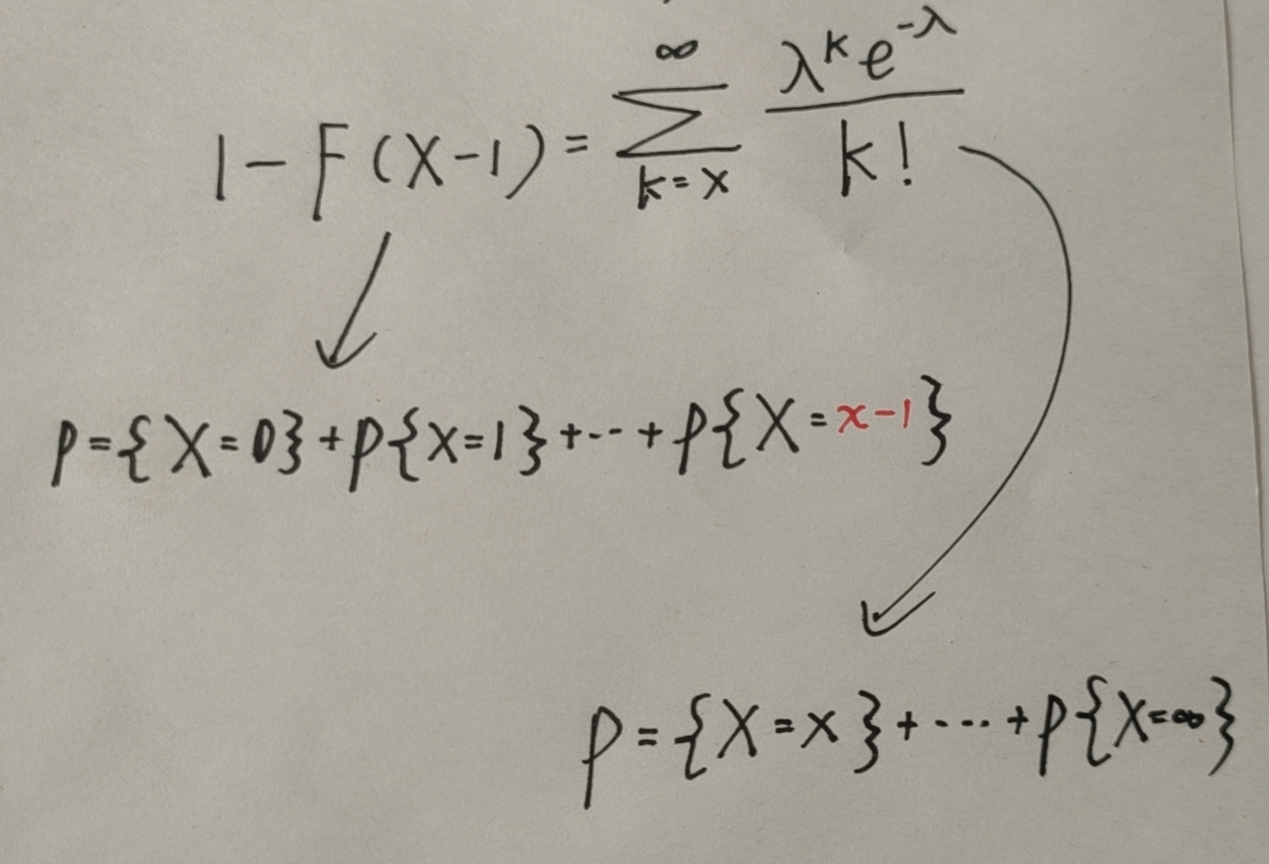
如何用泊松分布求二项分布的近似值（即用泊松分布来近似）

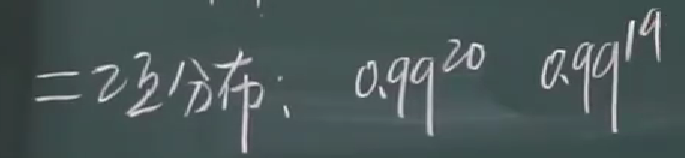
image-20220309211934527

适用条件：

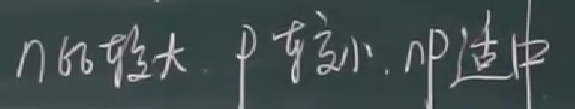
image-20220309212047830

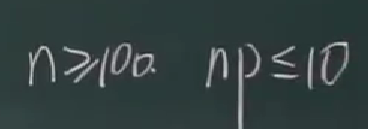
image-20220309212109296

例题

要准备多少现金x

\[np<=10可用泊松分布来近似，且\lambda=np=6 \]

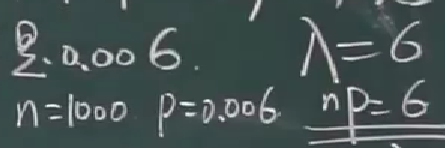
image-20220309213524518

image-20220309213451686

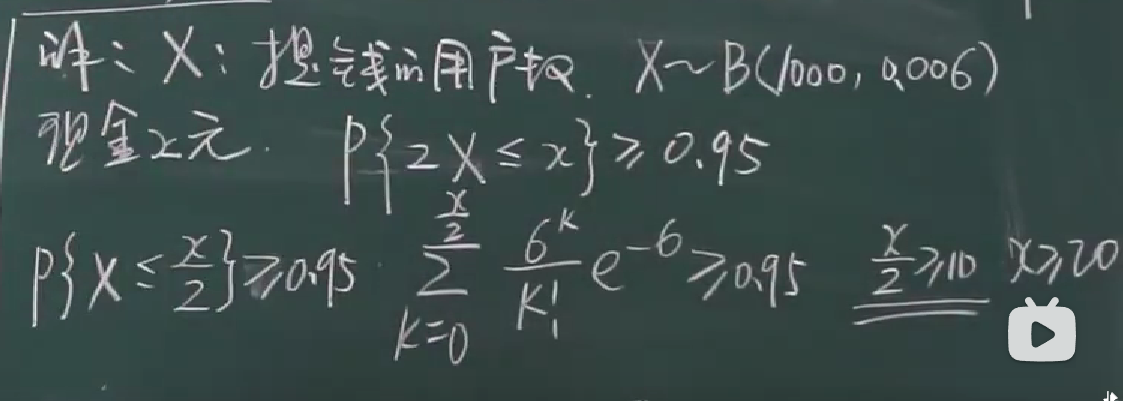
image-20220309213500120

查表

image-20220309214349812

从k=0开始加，发现加到k=10对应的数后，和大于0.95，说明x/2>=10

泊松分布例题

1.不超过5次的概率

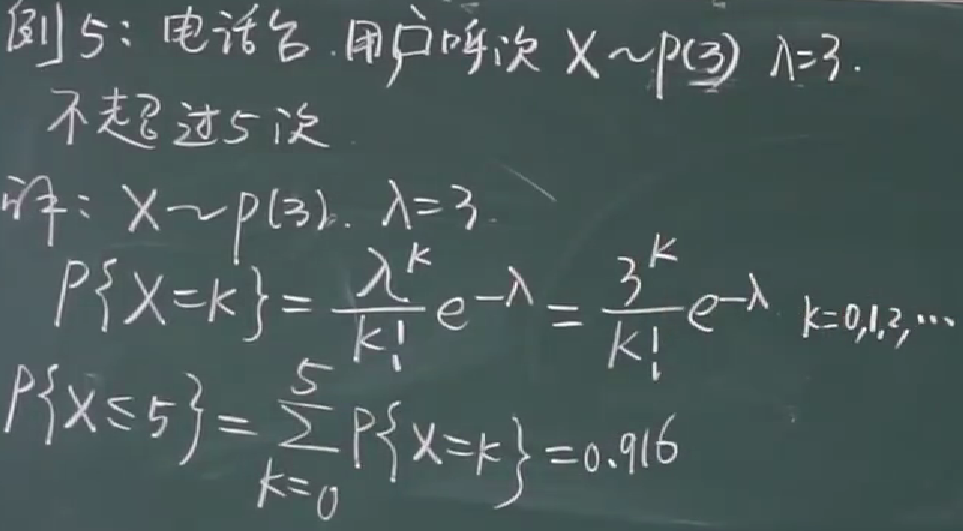
image-20220309212548965

2.二项分布用泊松分布来近似

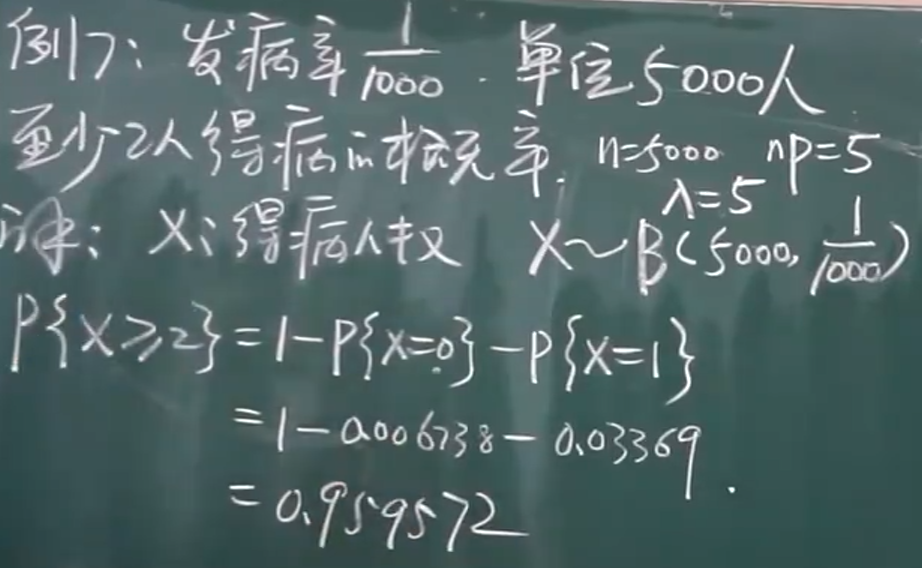
image-20220309220725413

超几何分布

引例

image-20220311211851862

定义

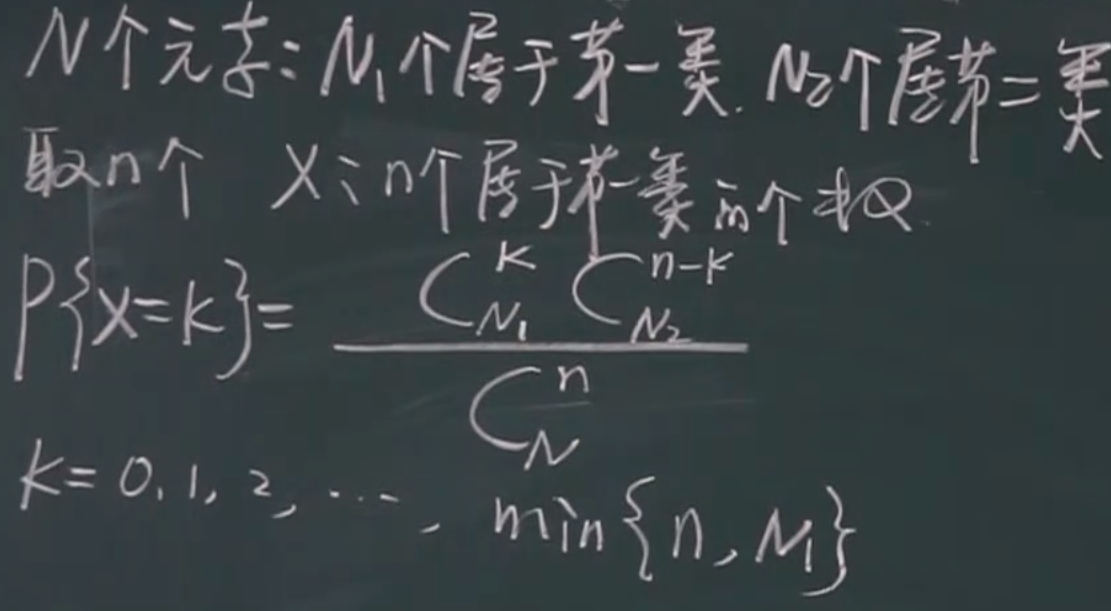
image-20220311212037438

例题

image-20220311212344872

对于不放回抽样实验，当总数N较大，抽样数量n较少时，超几何分布可以近似为二项分布（即抽取n=10粒种子，每个种子的发芽率都为p）

image-20220311215401649

例题

image-20220311221712902

N=10000，n=200，可将超几何分布近似为二项分布

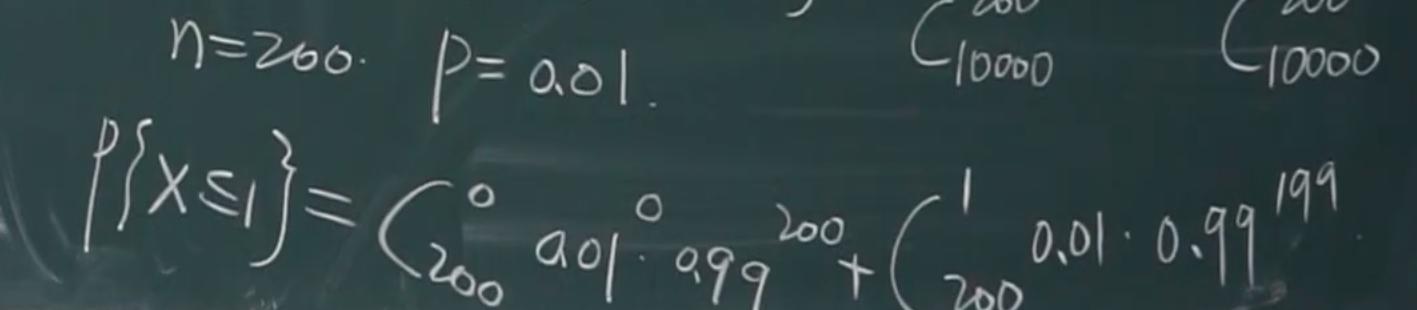
image-20220311221839654

n=200，p=0.01，np=2适中，可将二项分布近似为泊松分布

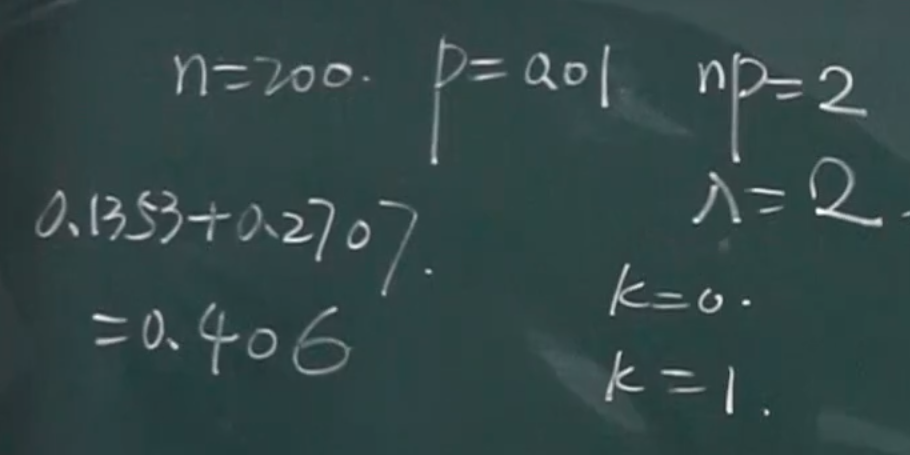
image-20220311222408823

本题总节

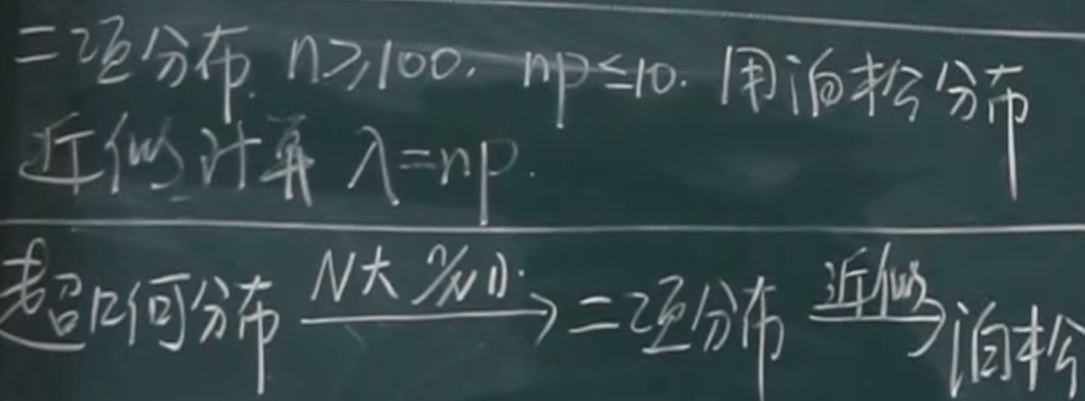
image-20220311222724926

2.连续性的分布

均匀分布

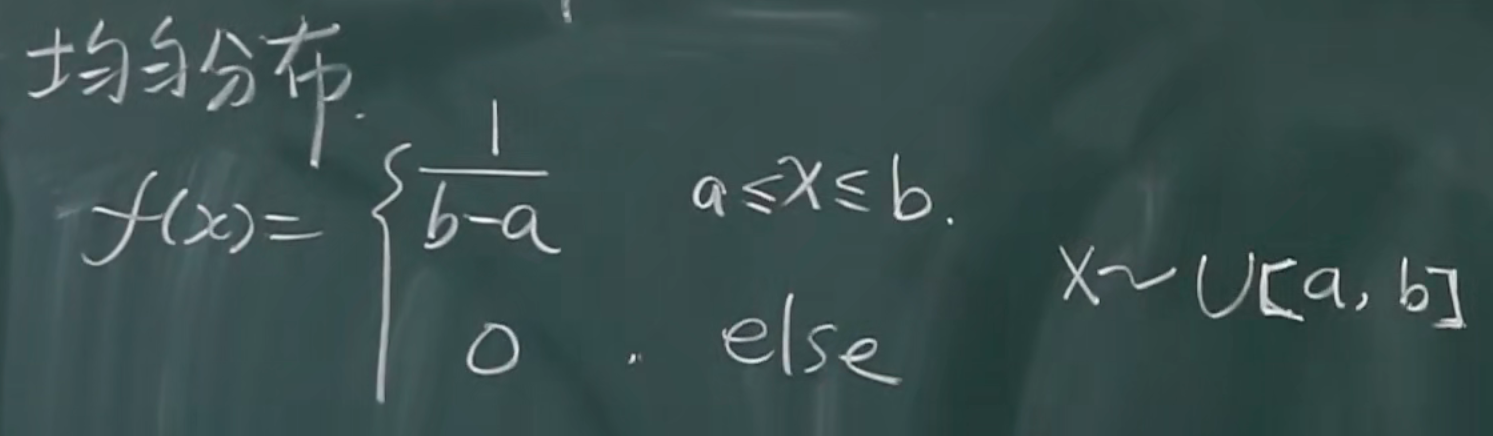
image-20220314101152316

概率密度函数下方的面积为1

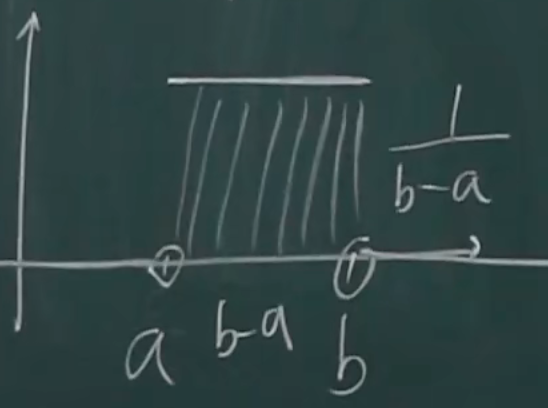
image-20220314101425943

均匀分布的 分布函数

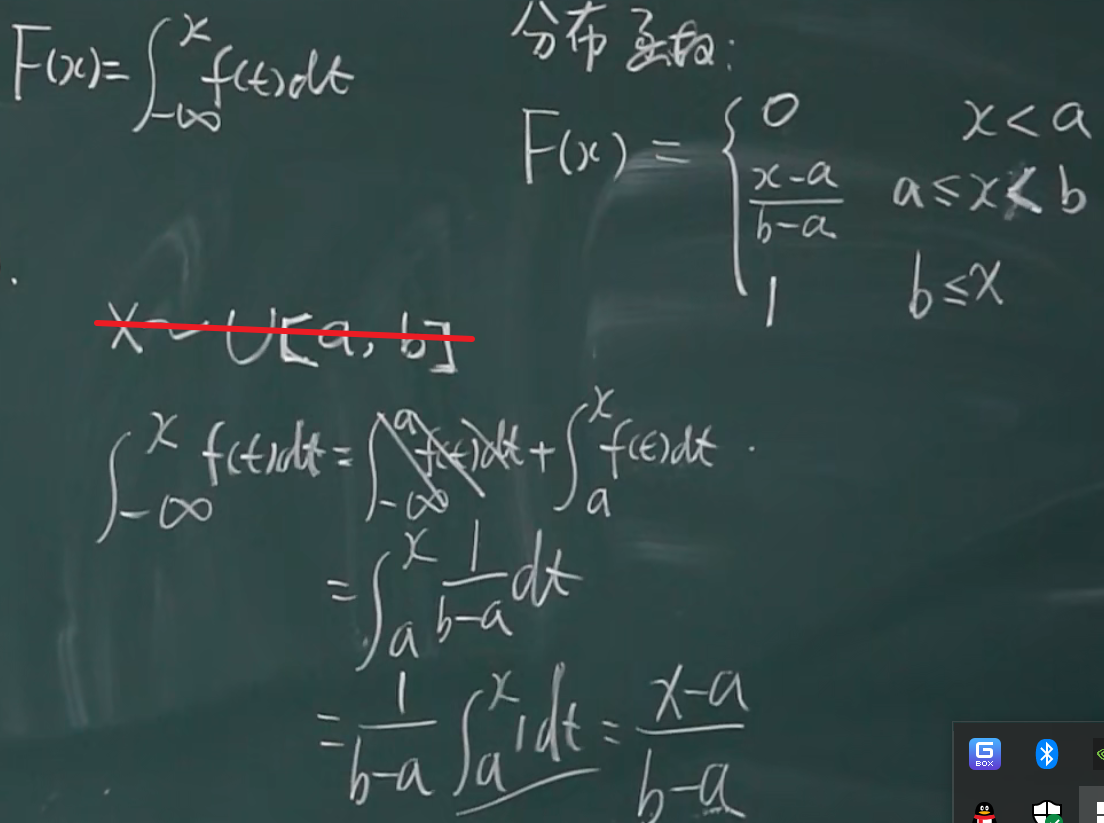
image-20220314101942909

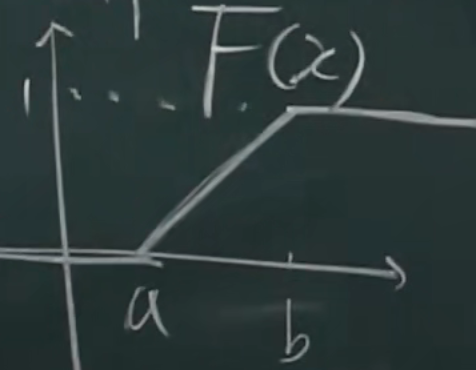
image-20220314102115343

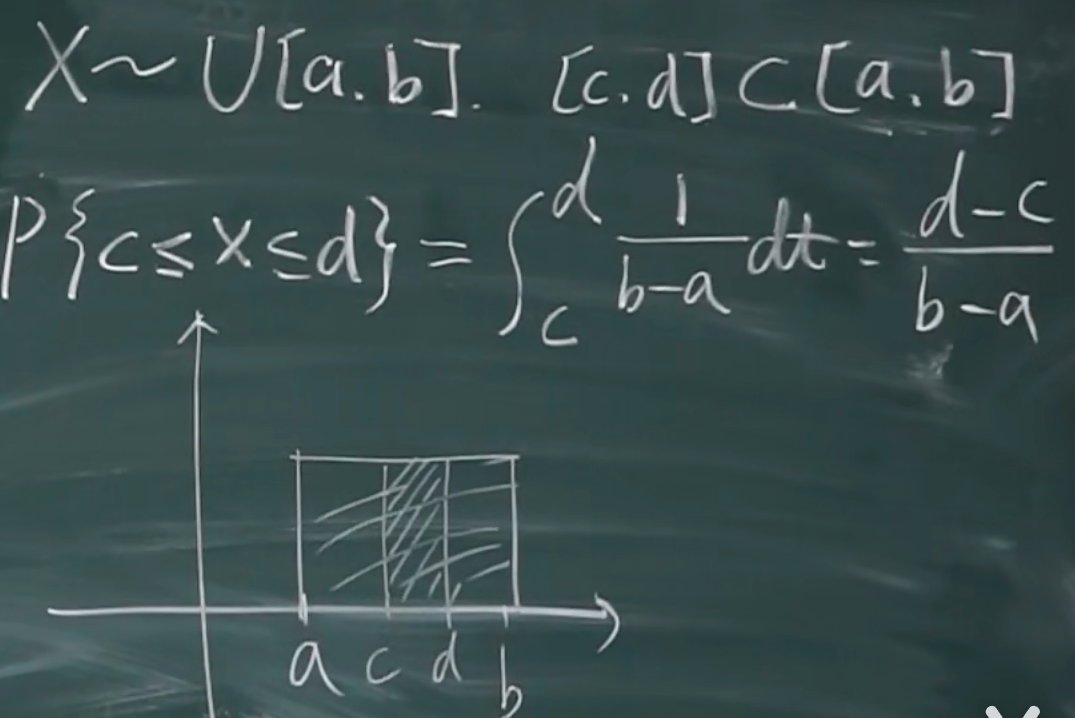
image-20220314102511677

例题

image-20220314103205615

指数分布

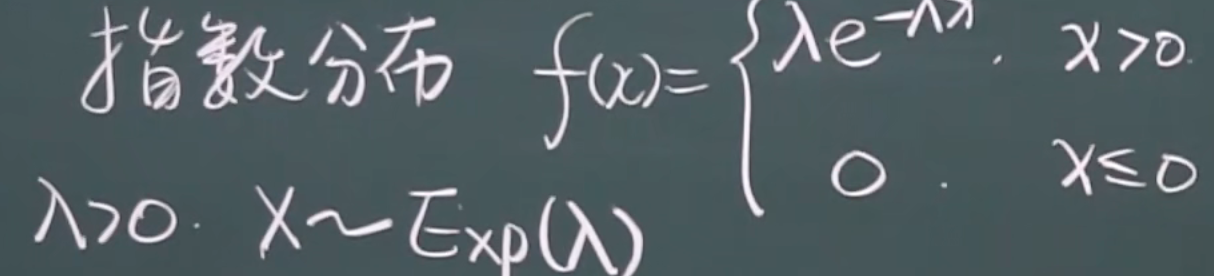
image-20220314103528934

概率密度函数

image-20220314103714886

指数分布的 分布函数

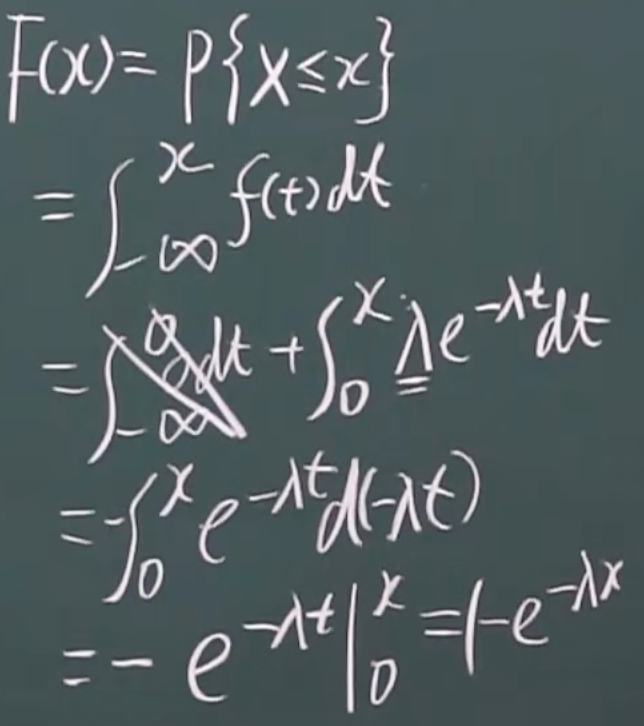
image-20220314103952825

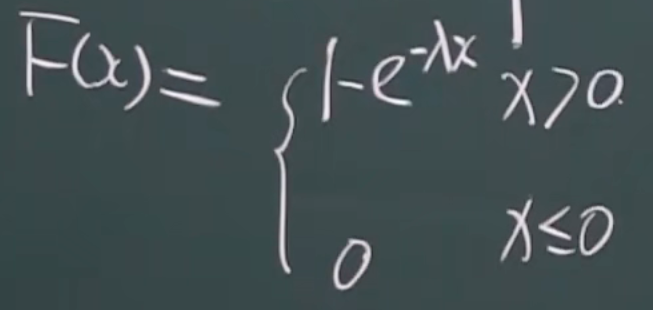
image-20220314104005955

例题

1.三个元件工作都大于1000小时

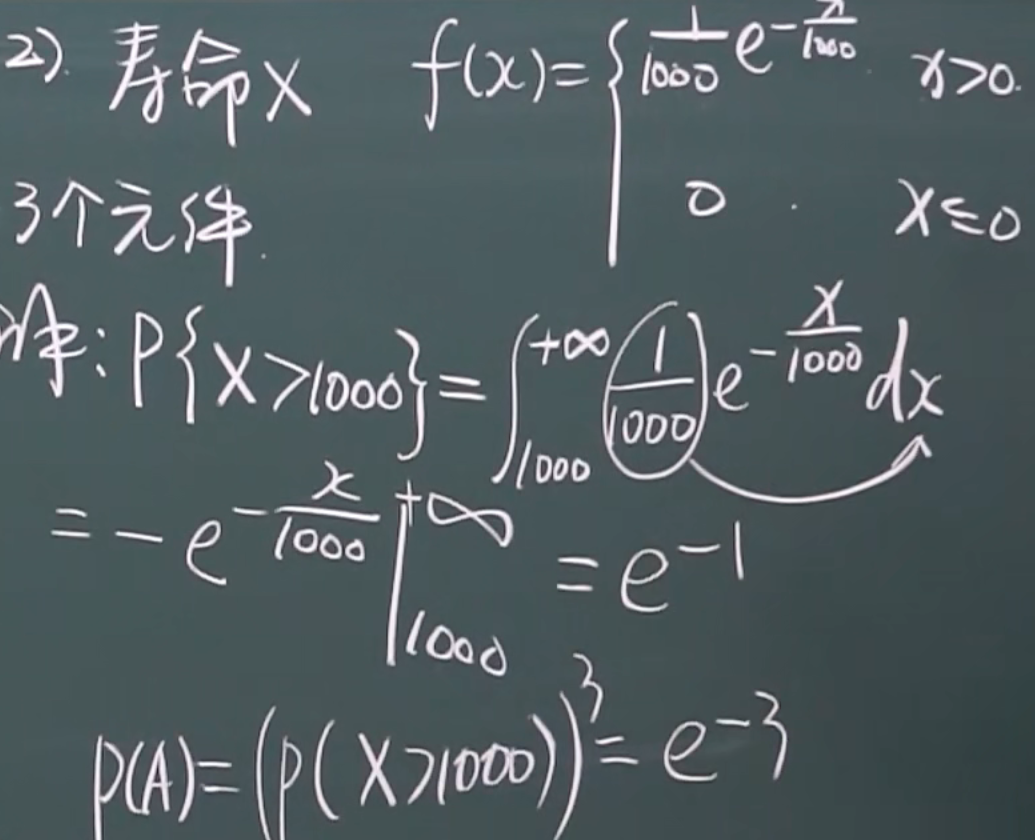
image-20220314104253372

无记忆性

某设备寿命为x，在时刻s，能再活t的概率与它现在的年龄s无关，称设备对已使用寿命无记忆性

即：p(活到t年)=p(再活t年|已经活了s年)

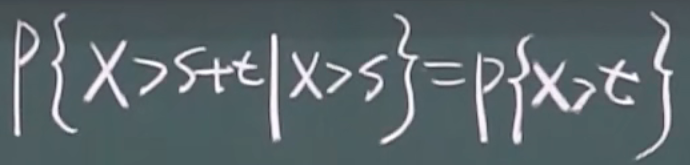
image-20220314105352756

eg：p(刚买的灯泡能用一年)=p(用了15年的灯泡再用一年)

例题

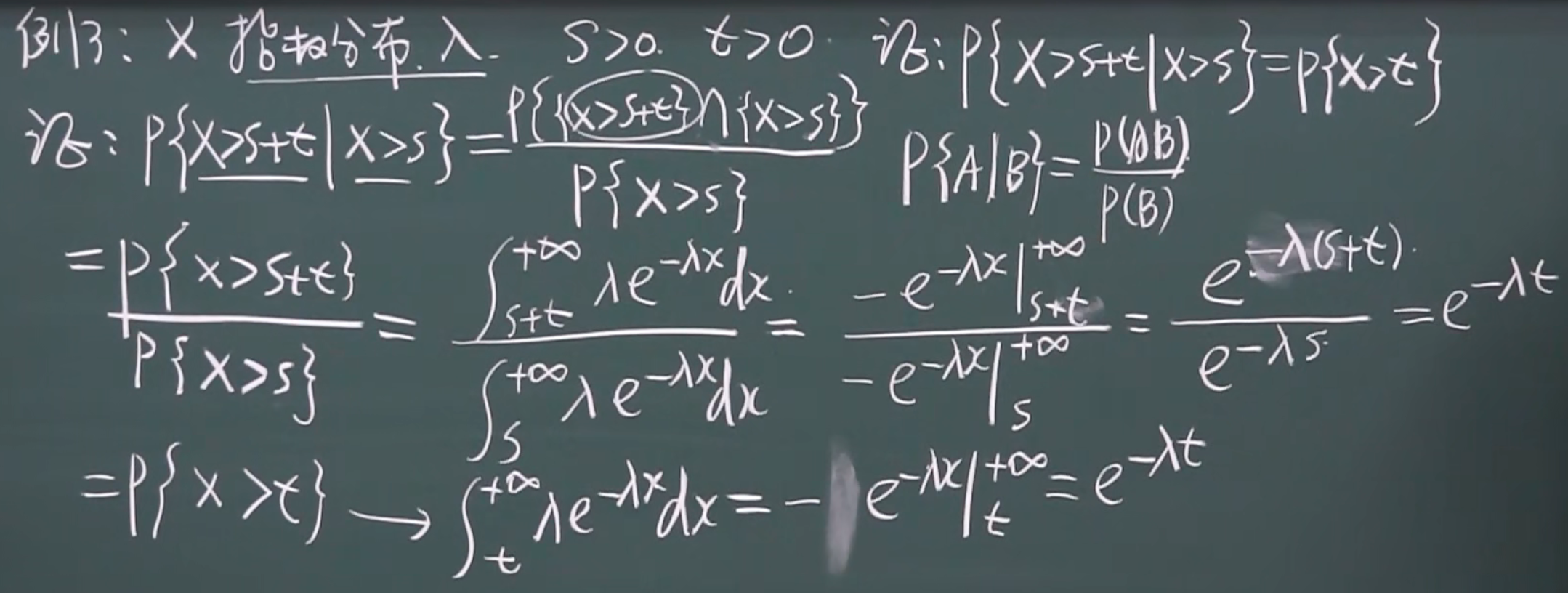
image-20220314213231999

画图解释

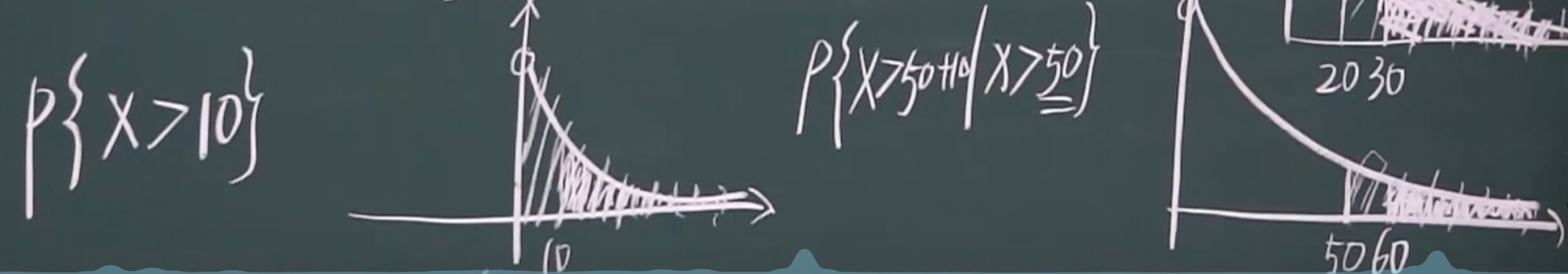
image-20220314213305655

正太分布

概率密度函数(小fai)

image-20220314213508729

分布函数(大fai)

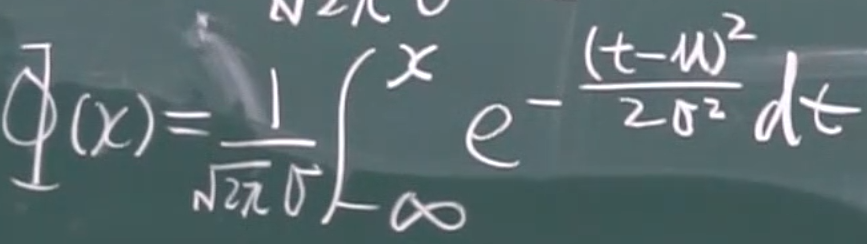
image-20220314214256974

性质

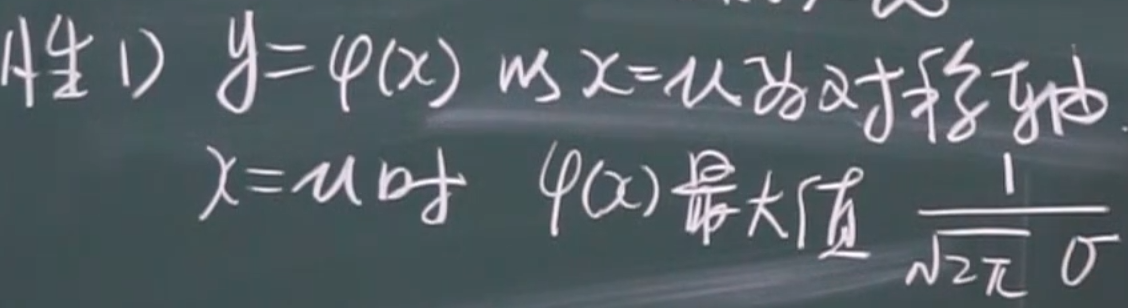
image-20220314214511258

image-20220314214725397

image-20220314214906990

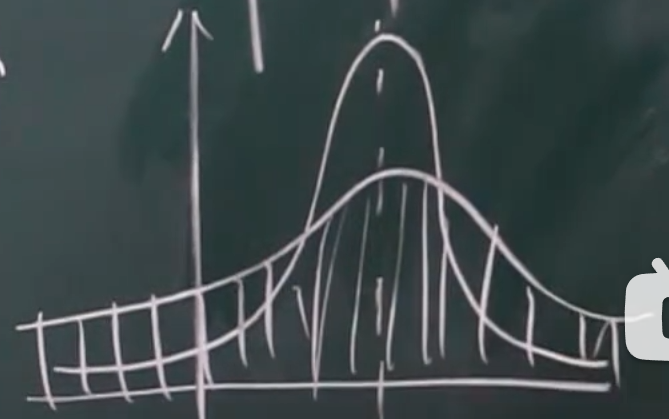
image-20220314215039307

标准正太分布

概率密度函数

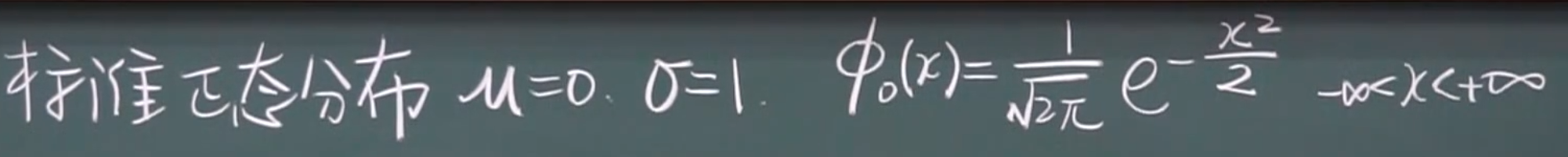
image-20220314215802033

分布函数

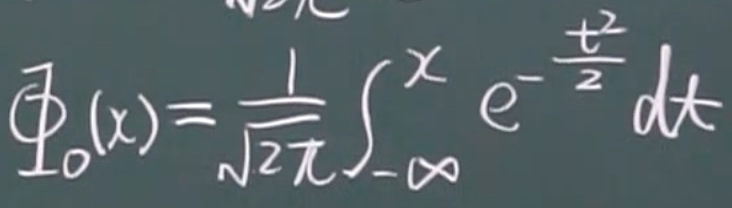
image-20220314215826310

性质

image-20220314220116693

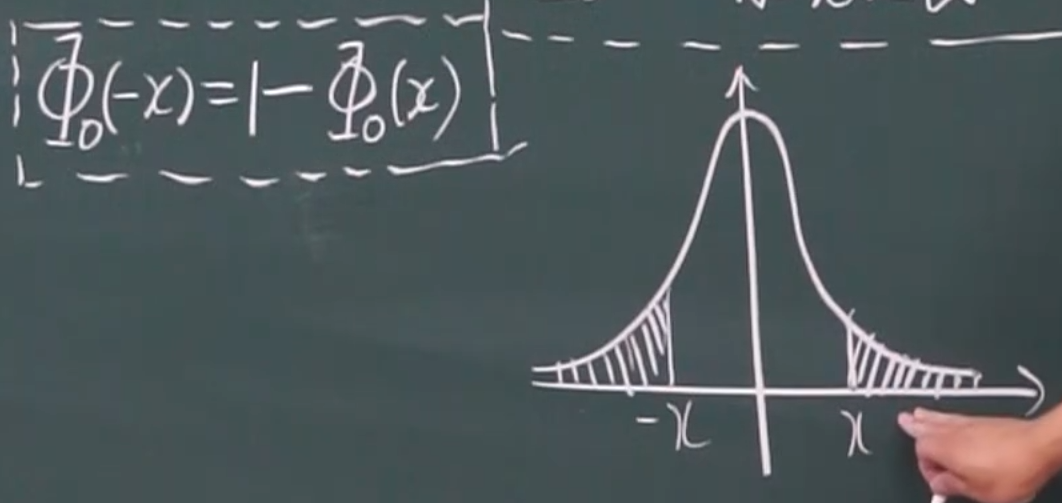
image-20220314220216540

计算：查表

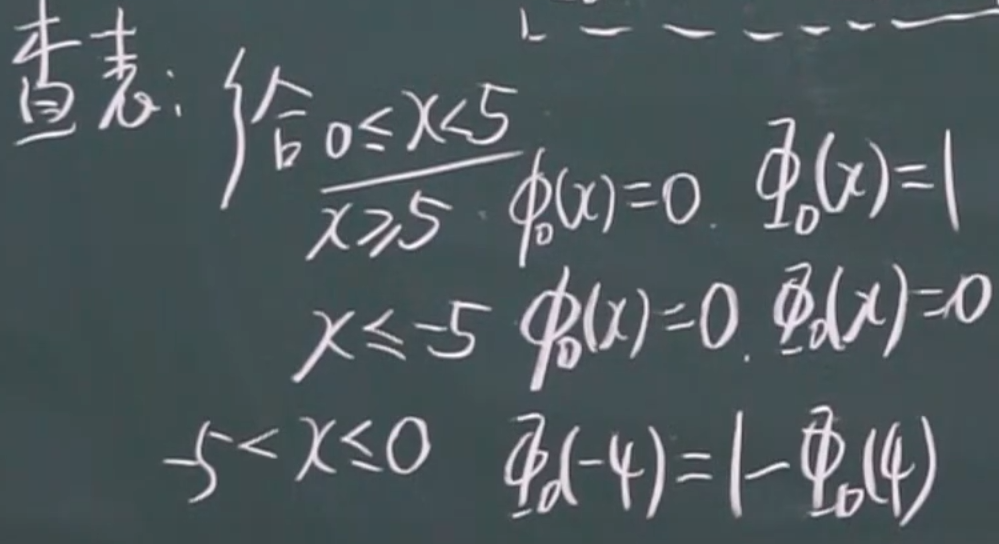
image-20220314220707585

如何将一般的正太分布化为标准的正太分布

概率密度函数的转化

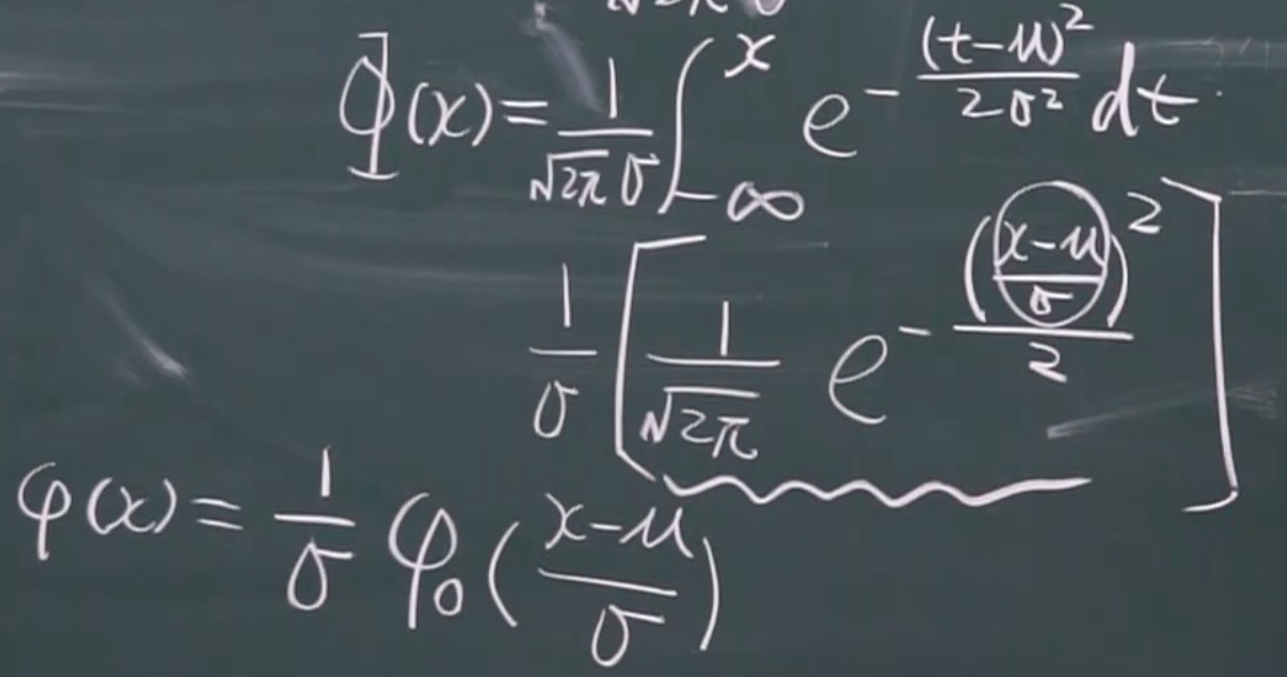
image-20220314221103940

分布函数的转化

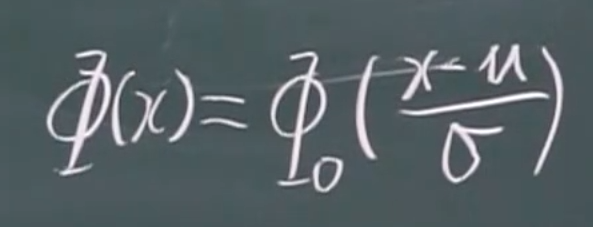
image-20220314221350243

公式

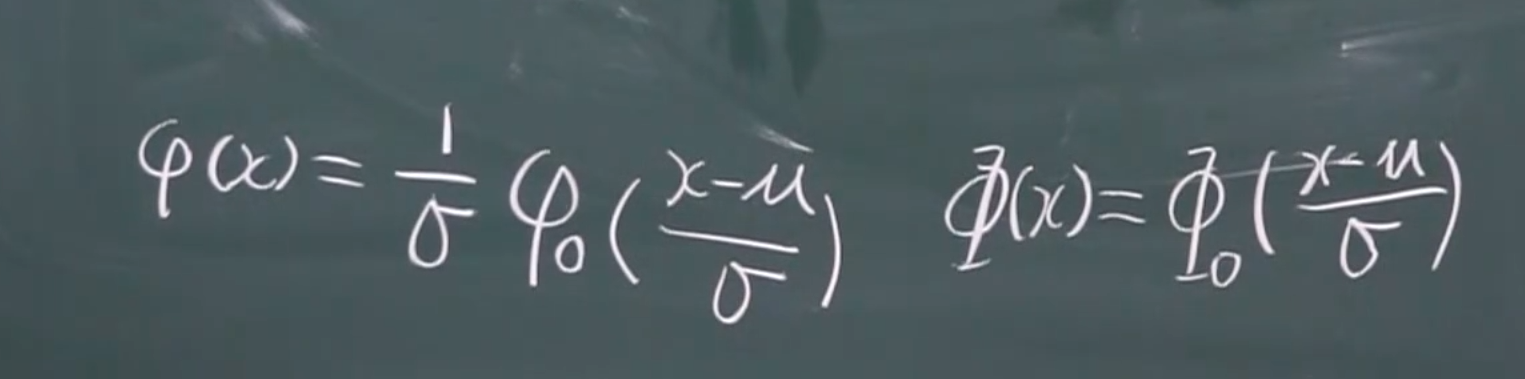
image-20220314221404803

例题

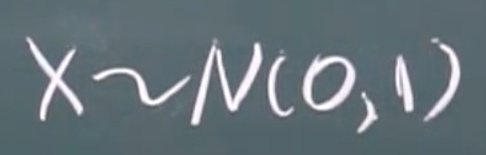
image-20220314221702473

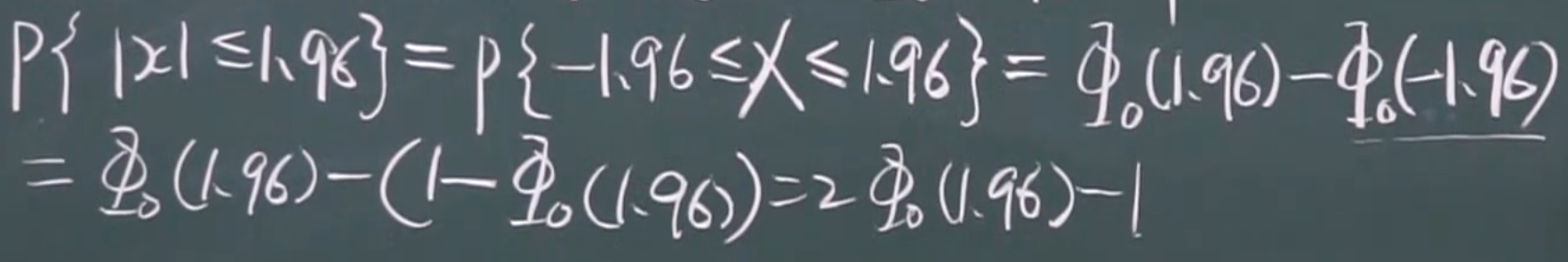
image-20220314221824432

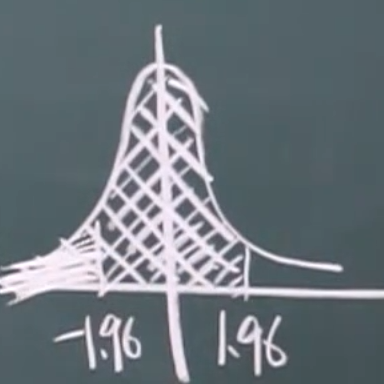
image-20220314221729285

2.！

(1)

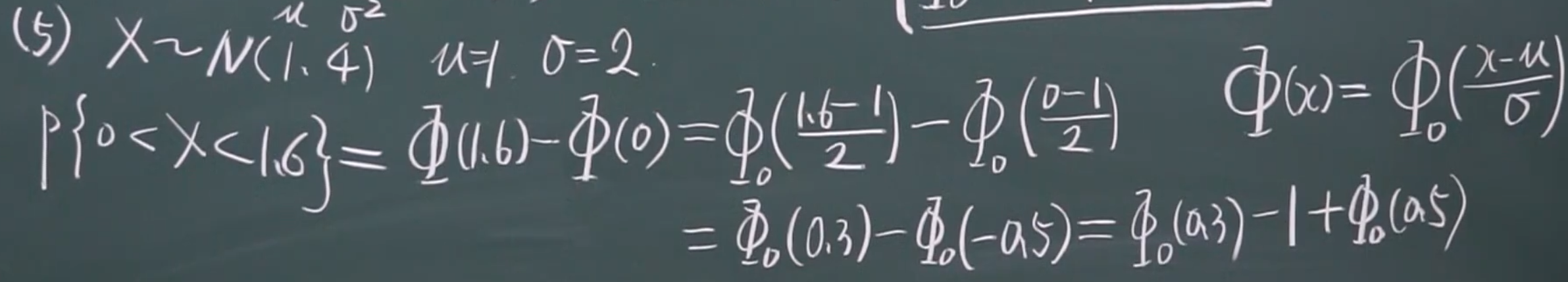
image-20220314222220904

(2)

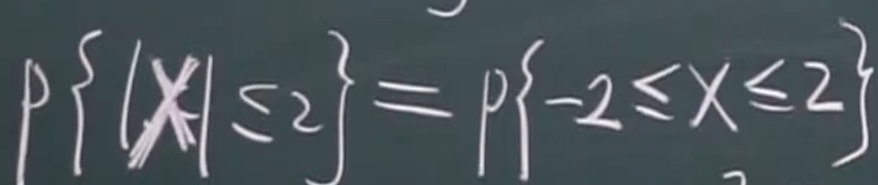
image-20220314222454984

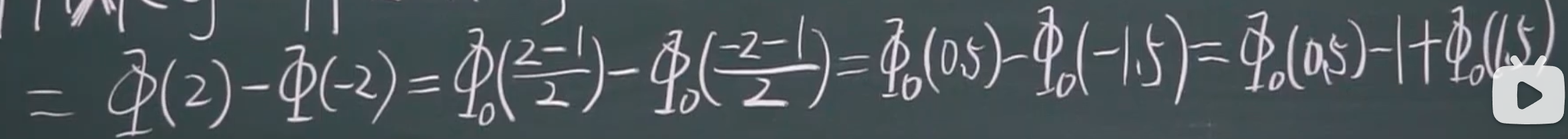
image-20220314222446969

方法二

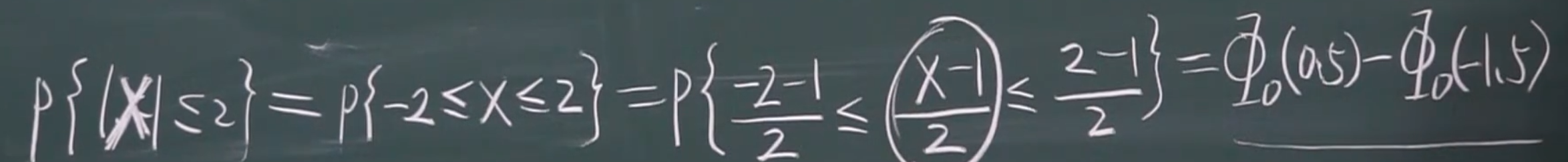
image-20220314223242344

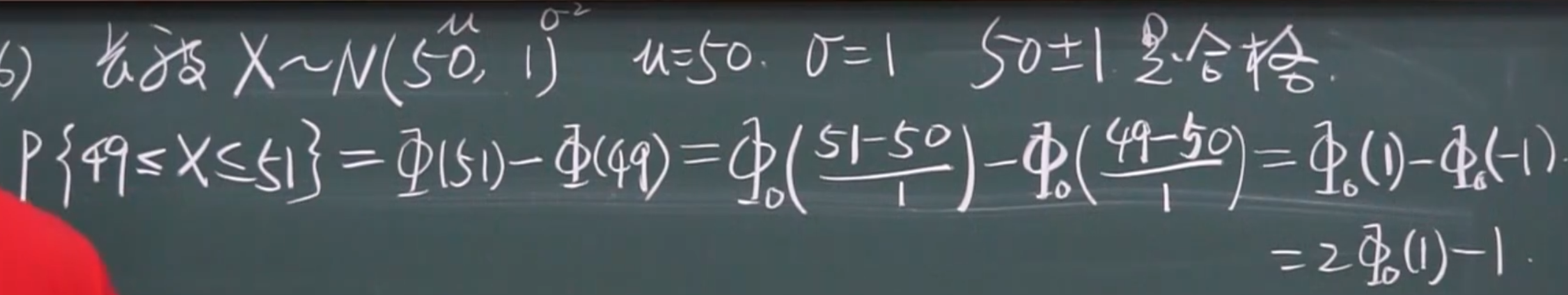
image-20220314223645331

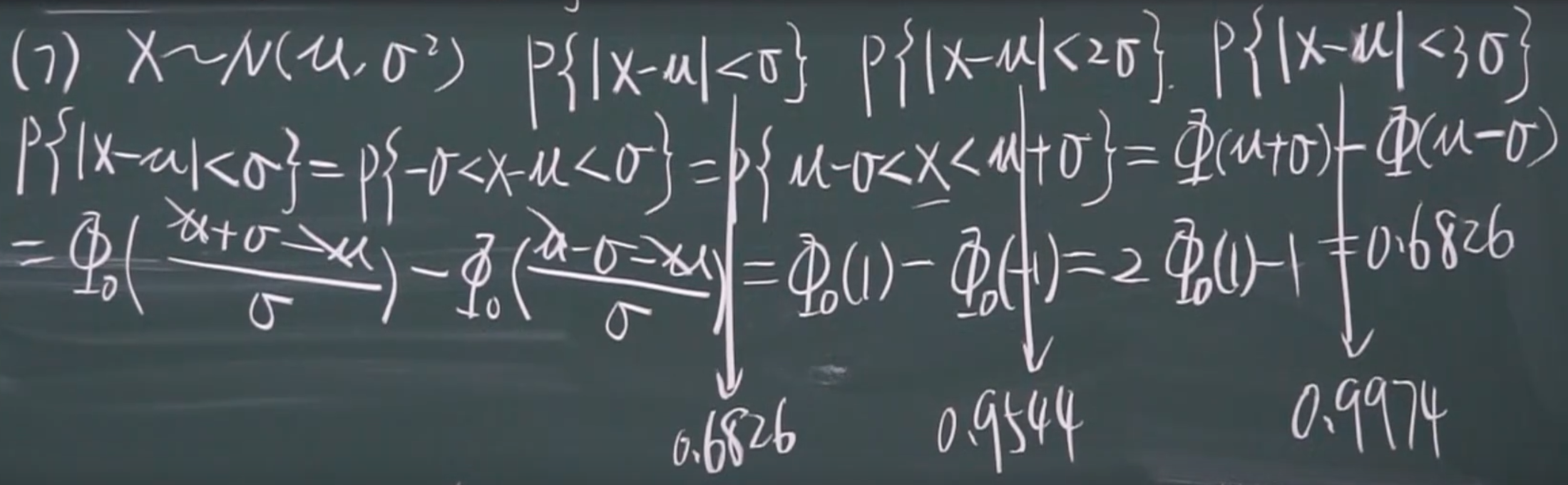
image-20220315093038976

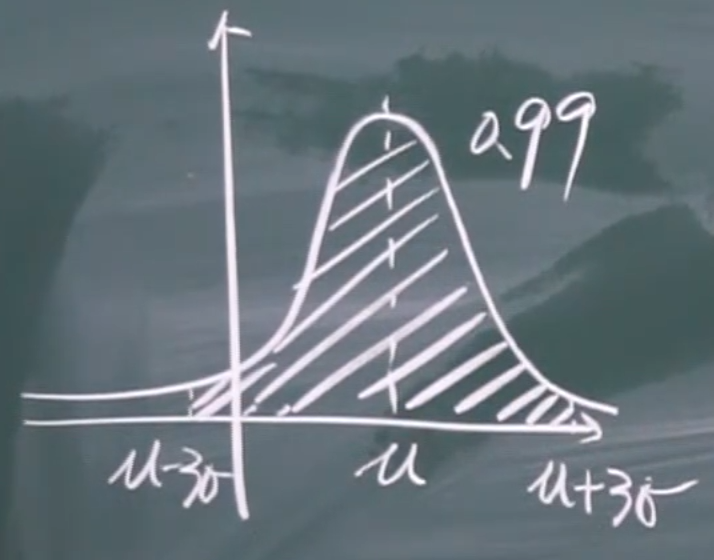
三\(\sigma\)准则

image-20220315095020889

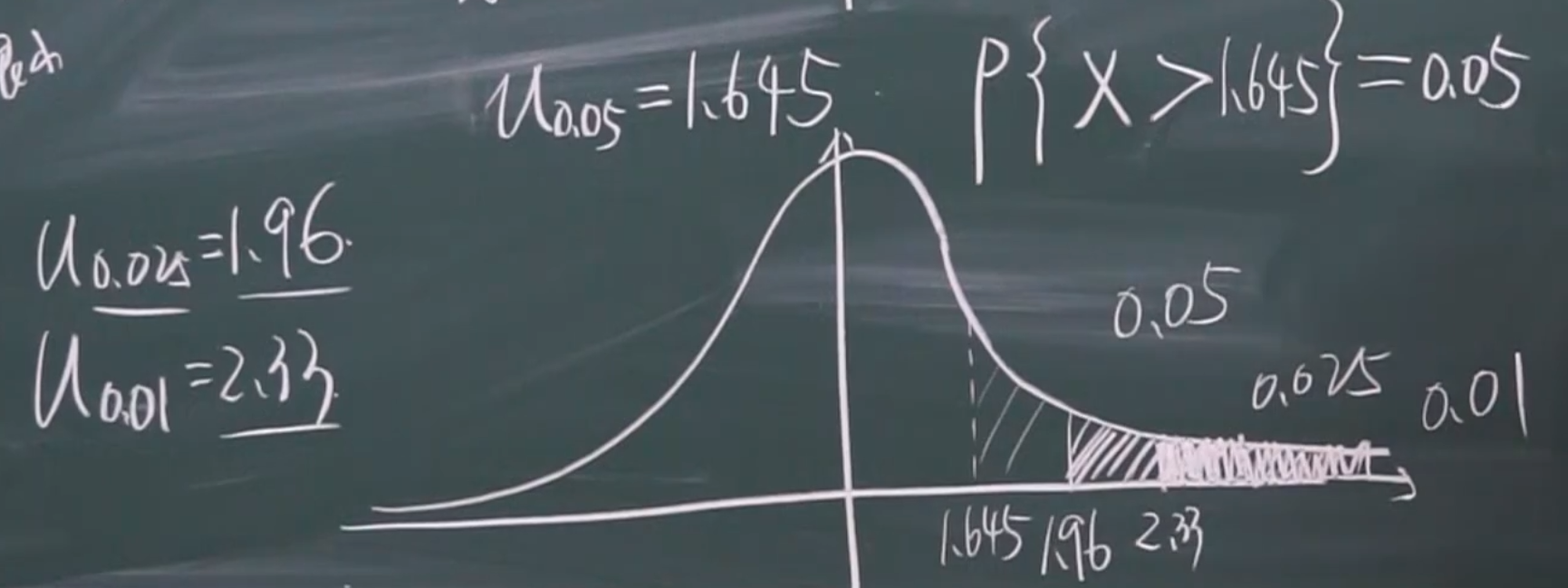
上\(\alpha\)分位数

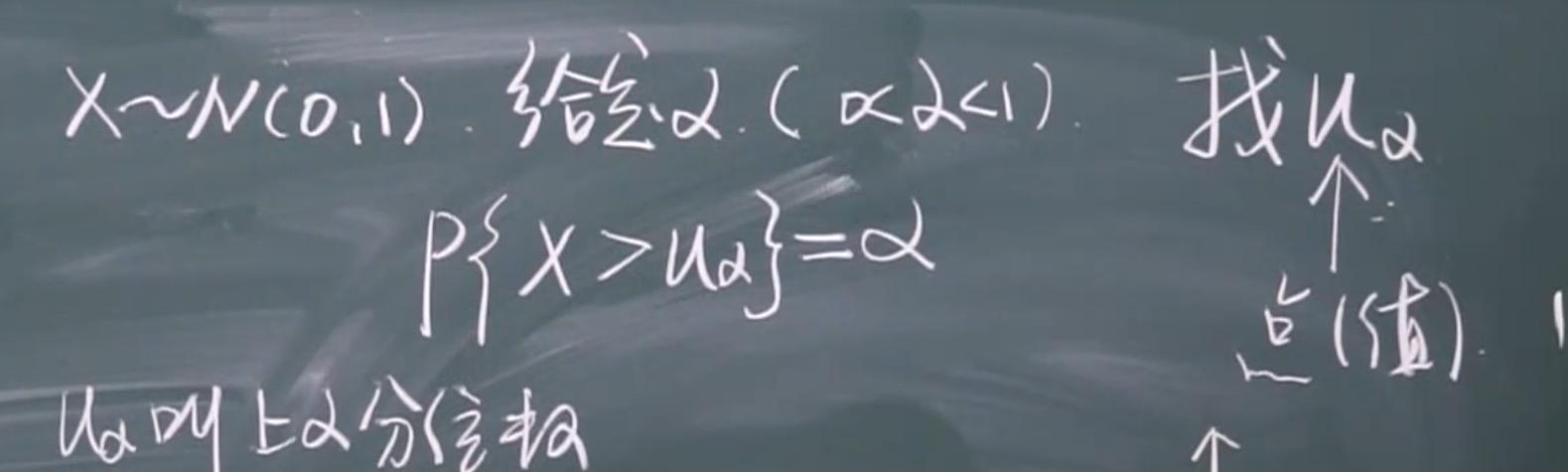
image-20220315095956114

\(u_\alpha\):上\(\alpha\)分位数

image-20220315100333528

2.3.1 离散型-随机变量函数的分布

image-20220315101448116

例子

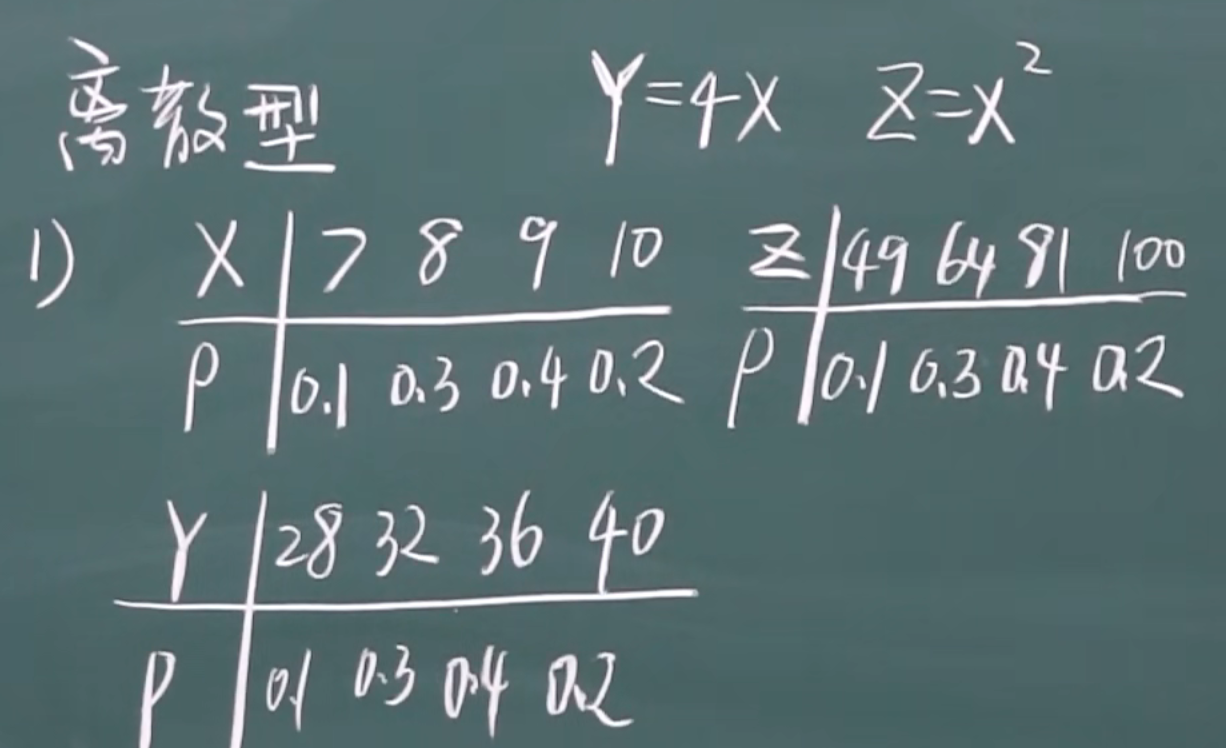
image-20220315101703022

image-20220315101934859

2.3.2 连续性-随机变量函数的分布

X的概率密度函数已知，Y是关于X的函数，求Y的概率密度函数

步骤

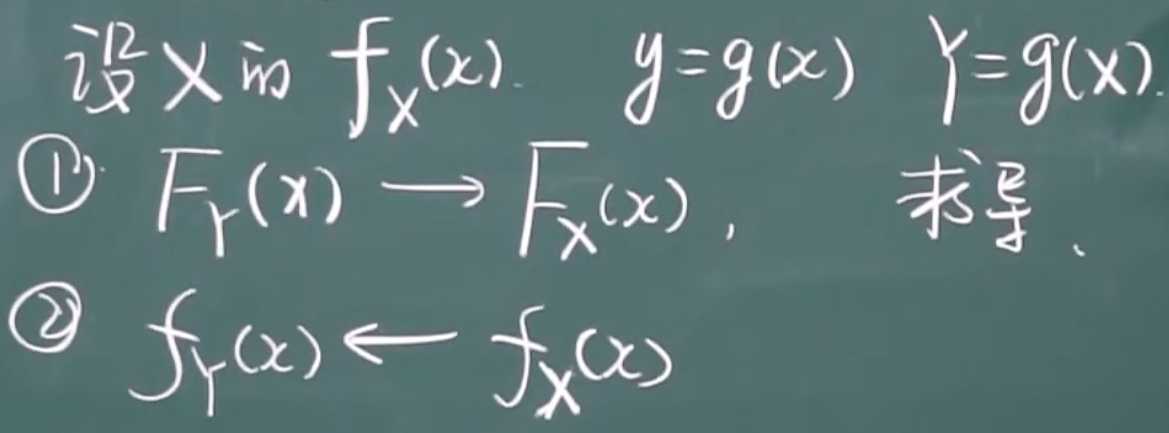
image-20220315102401221

公式

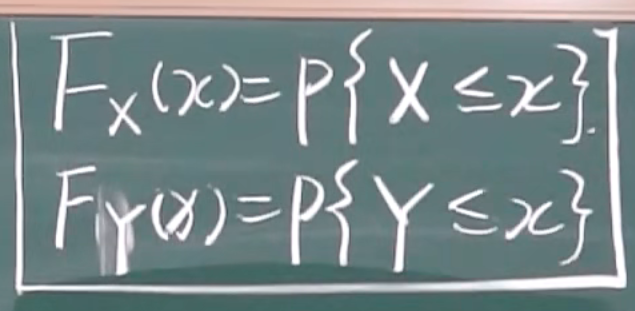
image-20220315113403339

例题

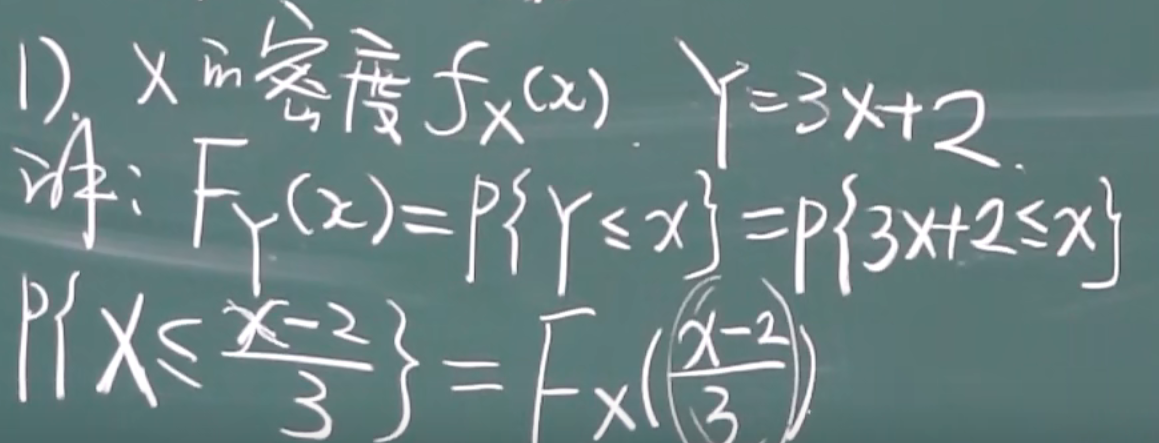
image-20220315125147201

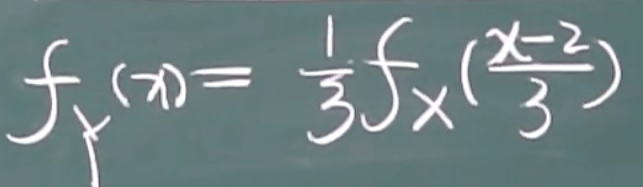
image-20220315125154151

具体的例子

1.X是均匀分布，Y是X的线性函数,Y=kX+c

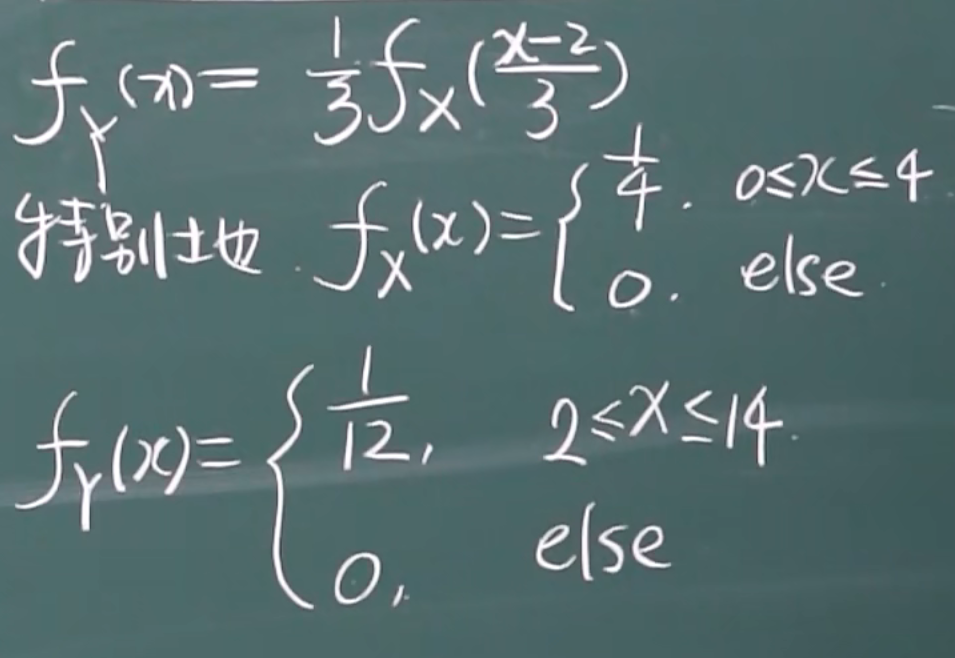
image-20220315125951821

结论：

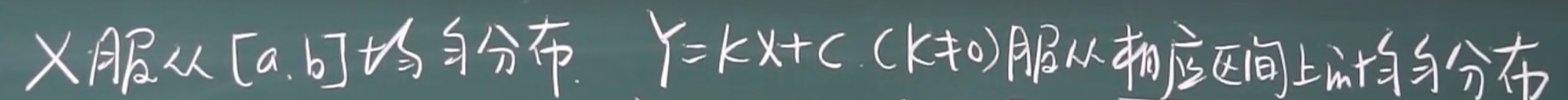
image-20220315130456352

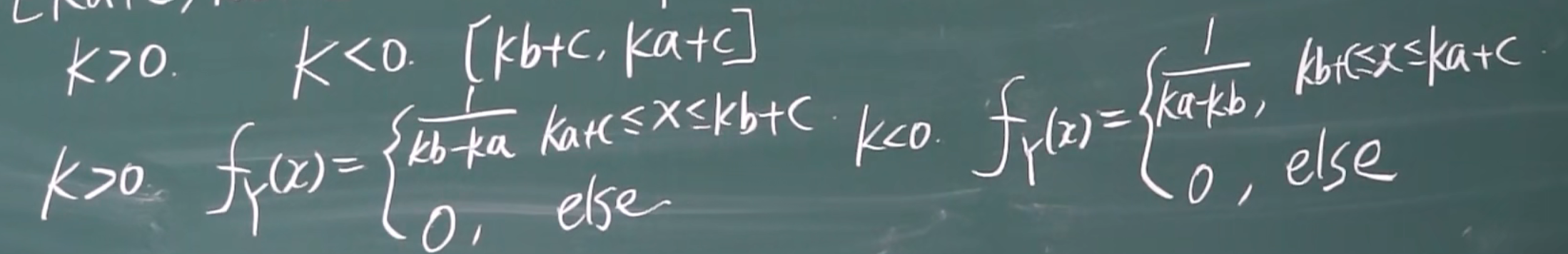
image-20220315130510585

2.X是正太分布，Y是X的线性函数，Y=kX+c

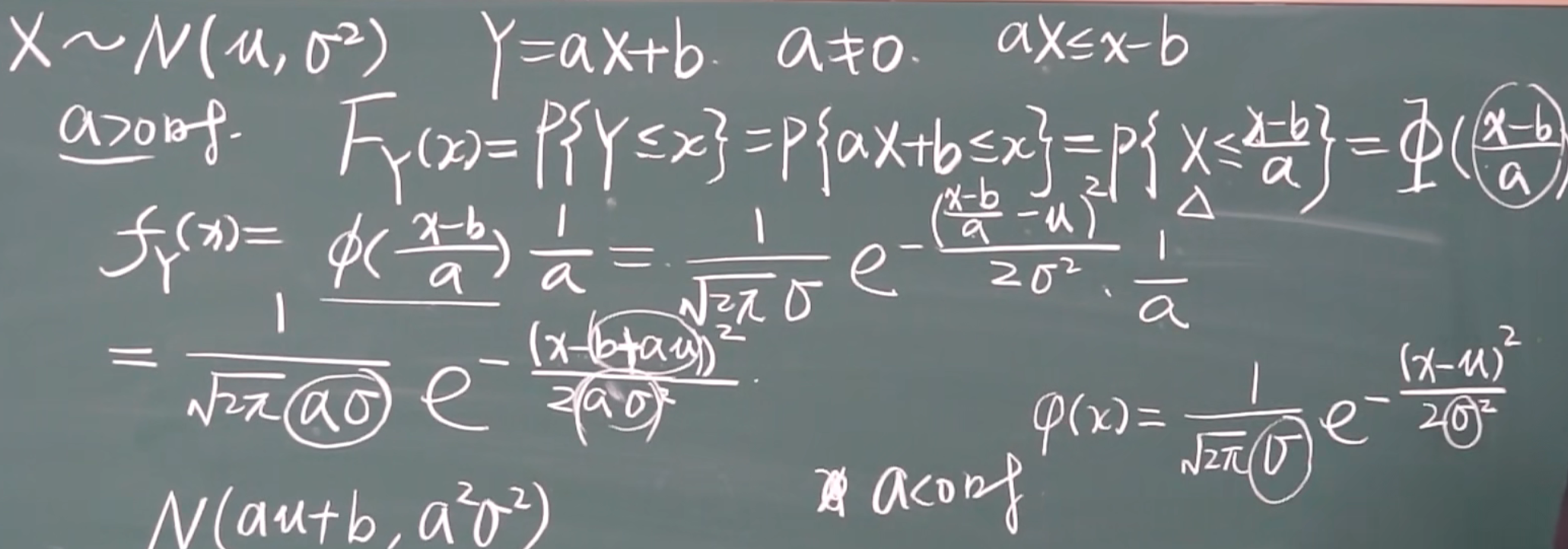
image-20220315132849772

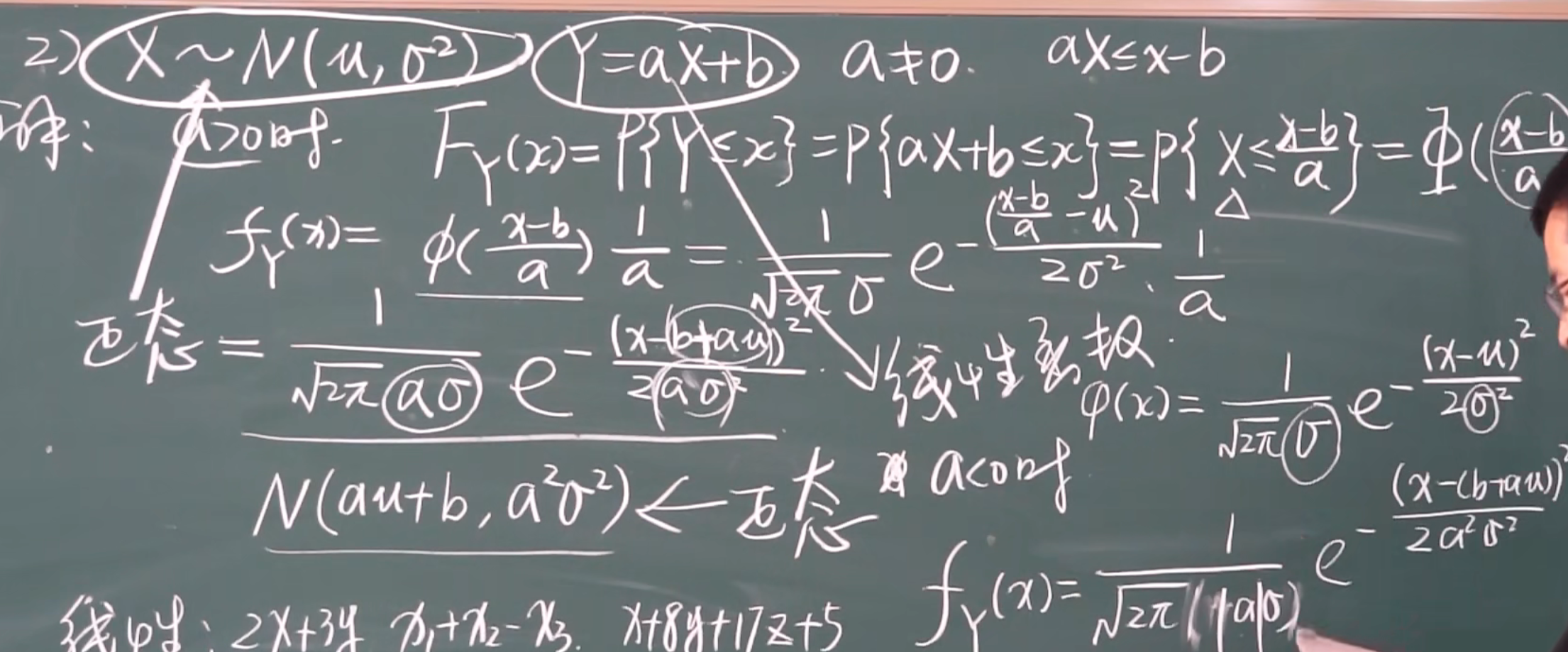
image-20220315132655761

特别的有：

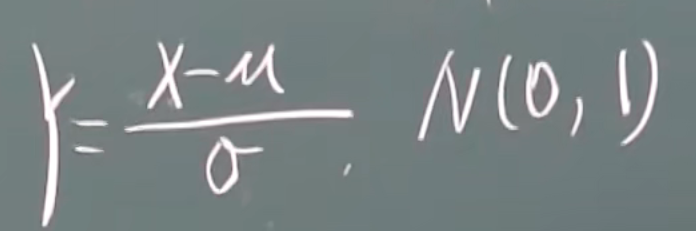
image-20220315134418850

3.X是标准正太分布，Y=X2

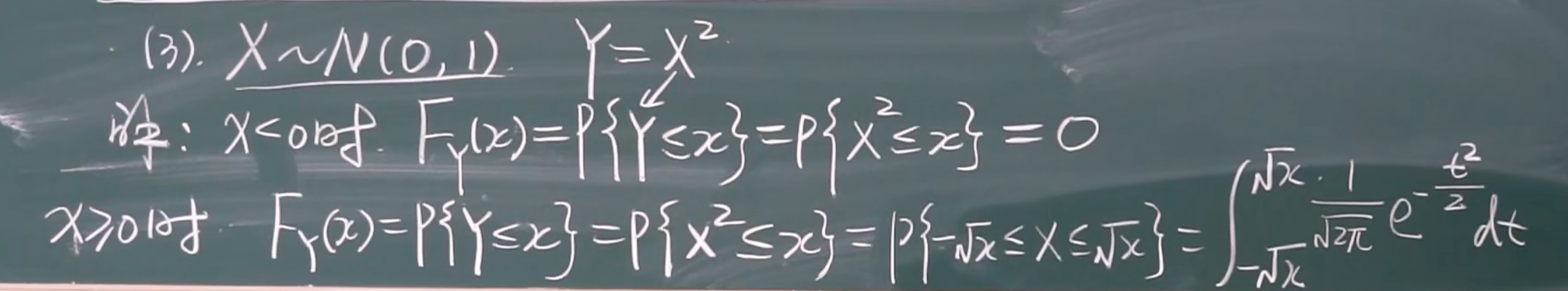
image-20220315140138534

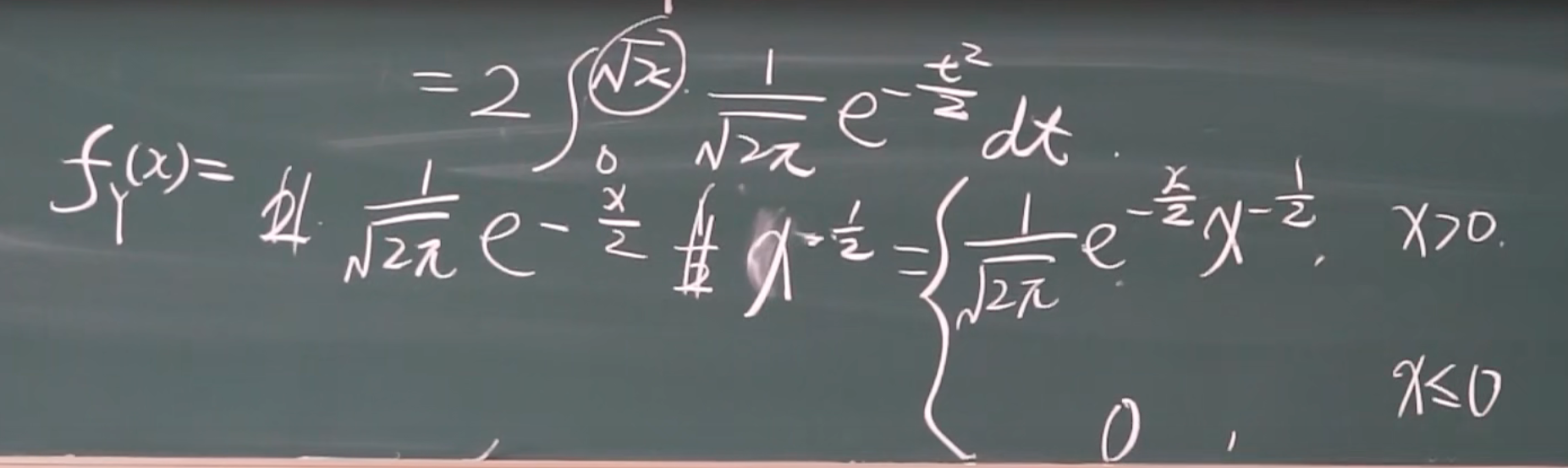
image-20220315140219454

定理

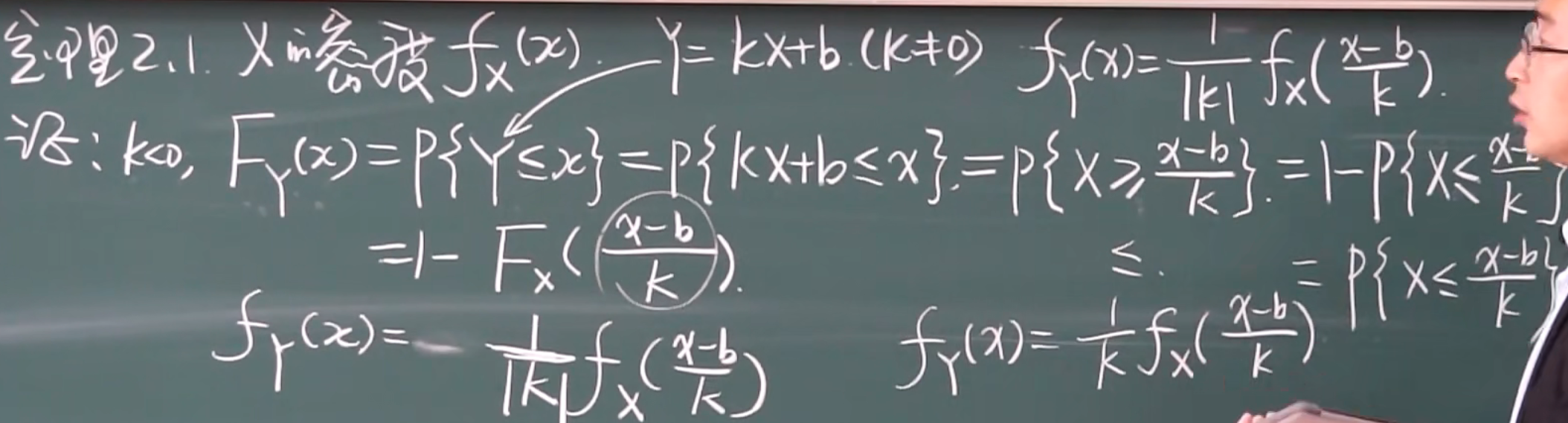
image-20220315134905440

posted @ 2022-03-29 13:35  Cornfield_Chase  阅读(344)  评论(0)    收藏  举报