第一章：概率论的基本概念

一.一 随机事件

1.1.1 随机实验与随机事件

随机实验

image-20220216141757250

事件 & 随机事件

image-20220216141850674

随机事件：可能发生也可能不发生的事件，用A,B,C表示

基本事件 ！

image-20220216142231965

复合事件 ！

image-20220216142548155

eg：扔色子：点数小于5

必然事件 & 不可能事件

image-20220216143439256

不可能事件的发生概率为 0，反之不成立

概率为 0 的事件也有可能会发生

eg：往0-1的线段上投质子投到 0.1处的概率为 0 ，但有可能发生

必然事件的发生概率为 1，反之不成立

概率为 1 的事件也有可能不会发生

eg：往【0，1】的线段上投质子投到（0，1）间的概率为 1 ，但有可能不发生

1.1.2 样本空间与事件的集合表示

样本空间 & 样本点

image-20220217134610457

样本点即为基本事件

事件的集合表示

色子的点数为偶数点：

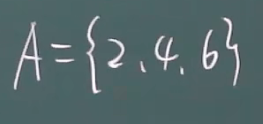
image-20220217135518450

小结

image-20220217135700107

1.1.3 事件间的关系

包含

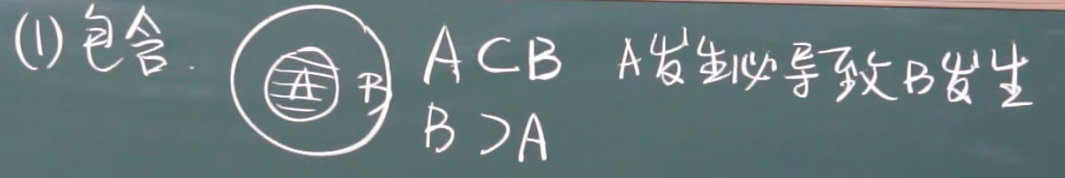
image-20220217140504809

一定成立：

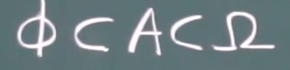
image-20220217140523282

事件相等：

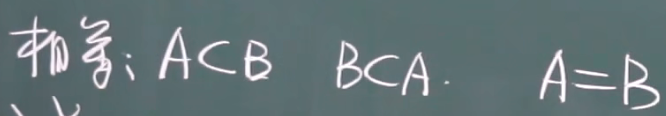
image-20220217140725224

并（和）

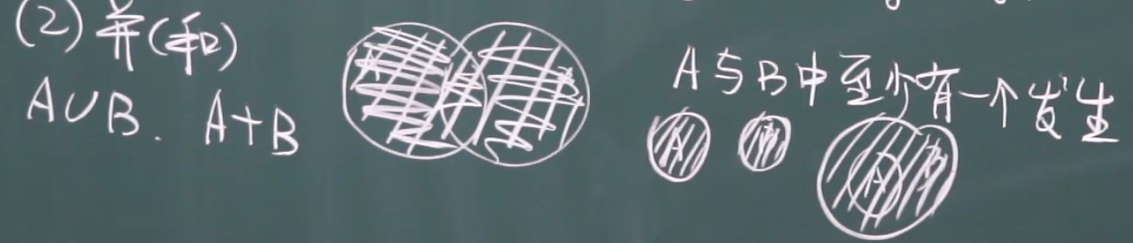
image-20220217140916703

交（积）

image-20220217141159180

差

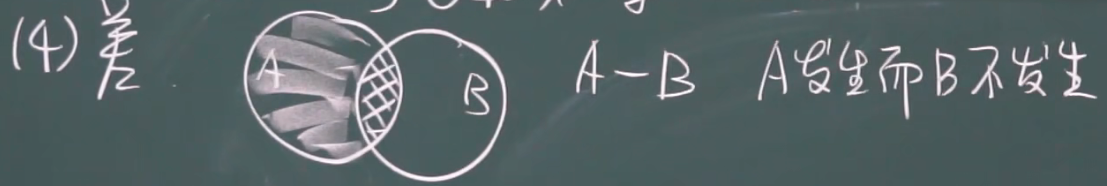
image-20220217142846613

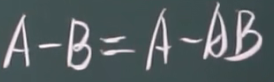
image-20220217143018014

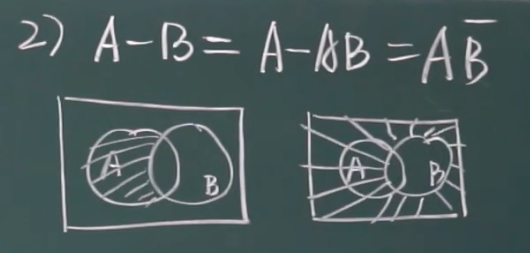
image-20220217144053536

互不相容事件

image-20220217143335531

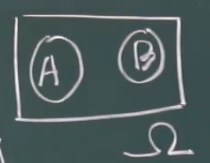
image-20220217143758744

对立事件

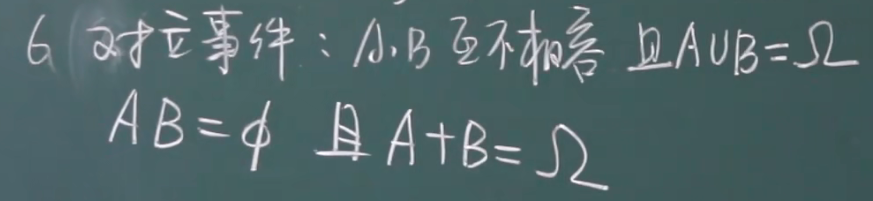
image-20220217143719427

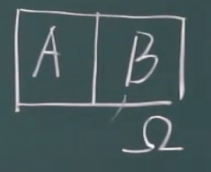
image-20220217143806568

记作：

image-20220217143911876

互不相容，对立的联系与区别

image-20220217144534752

完备事件组

image-20220217144746753

事件间的运算律 ！

image-20220217151047249

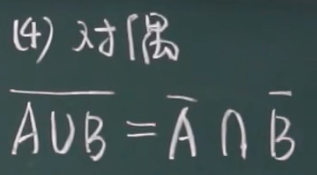
image-20220217151503656

A，B都没发生 = A没发生 且 B没发生

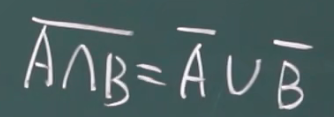
image-20220217151535454

A，B不都发生 = A没发生 或 B没发生

*无限可列个

image-20220217141547705

可列举例：

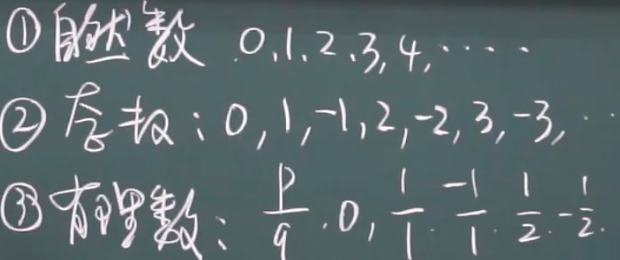
image-20220217142600721

不可列举例：

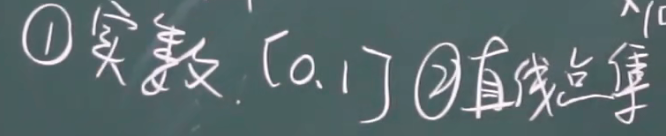
image-20220217142626034

一.二 事件的概率

1.2.1 概率的初等描述

image-20220218155227888

性质：

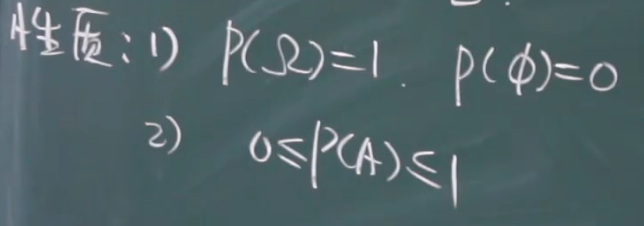
image-20220218155349764

1.2.2 古典概型

image-20220218161549167

image-20220218161724915

排列组合

image-20220218162300600

排列

image-20220218163836244

image-20220218163917794

组合

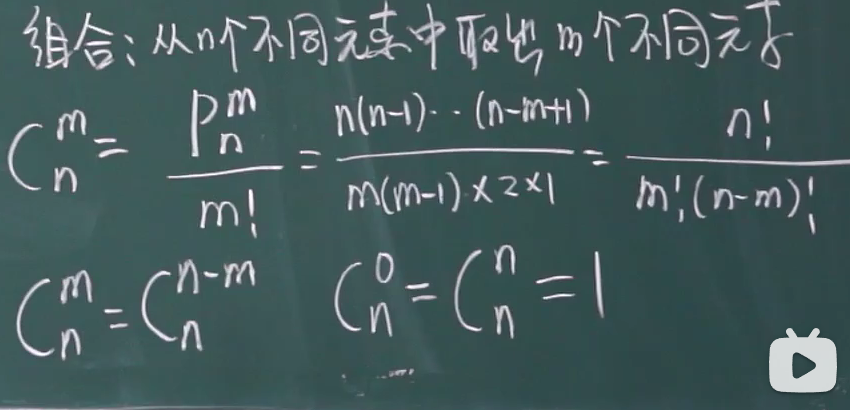
image-20220218164553754

古典概型性质

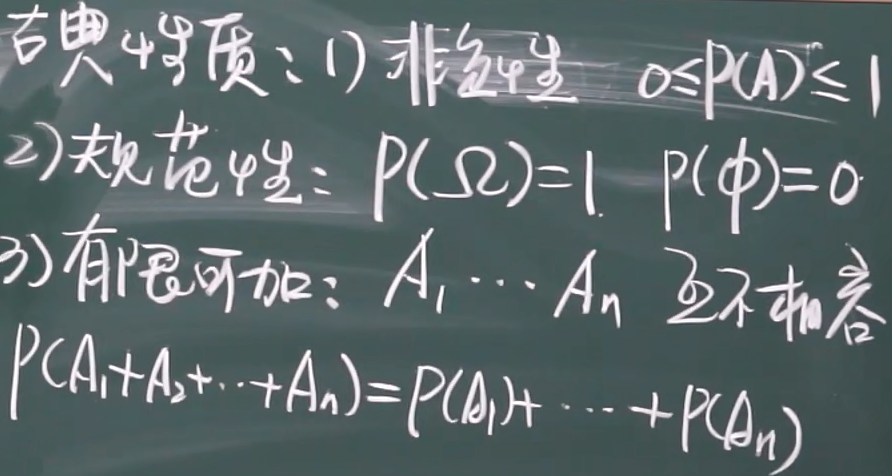
image-20220218222143869

缺点：（1）有限个结果（2）等可能性

1.2.3 几何概型

1.相遇问题

2.蒲丰投针问题

具有完全可加性（古典概型具有有限可加性）

1.2.4 频率与概率

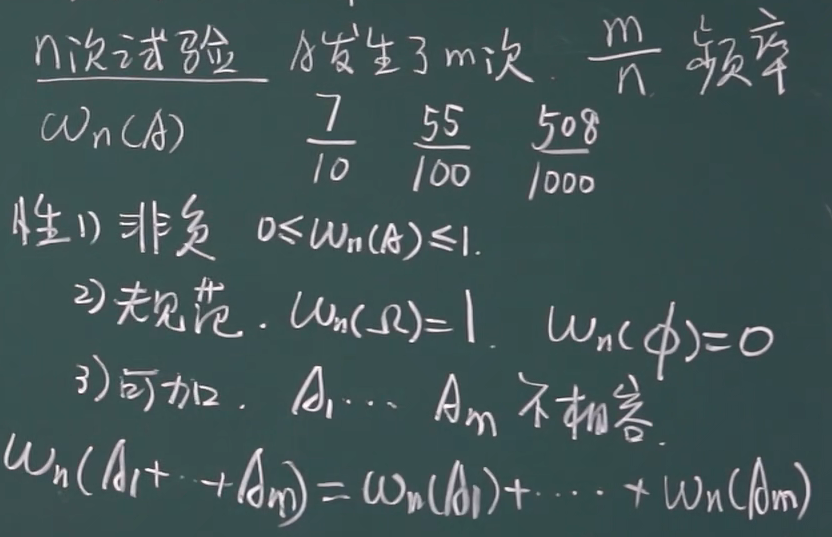
image-20220219143314962

概率可以理解成理想值，频率是实验值

概率先于频率而客观存在

1.2.5 公理化 ！

公理

image-20220219161205890

性质

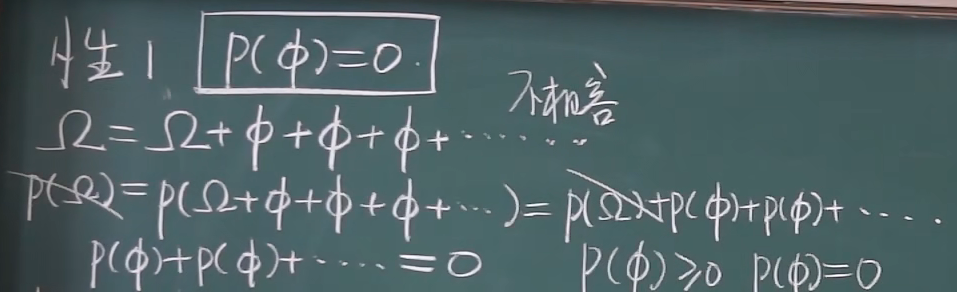
image-20220219161453926

不可能事件的发生概率为 0，反之不成立

概率为 0 的事件有可能会发生

eg：往0-1的线段上投质子投到 0.1处的概率为 0 ，但有可能发生

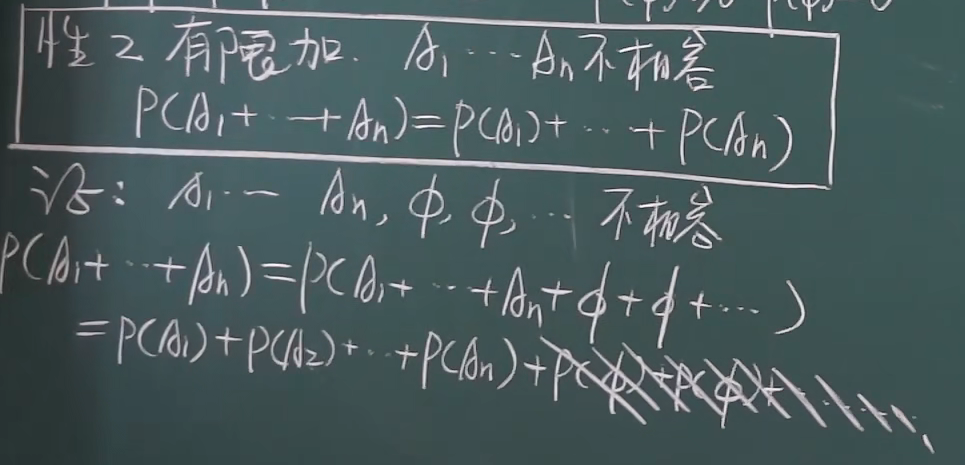
image-20220219161620693

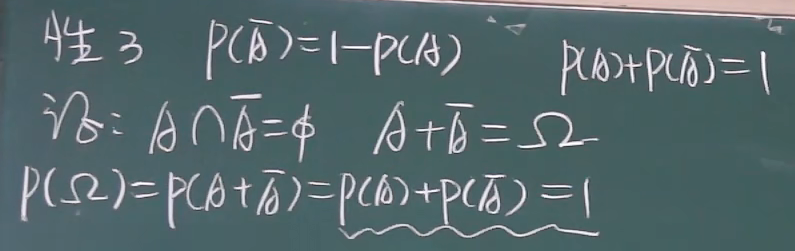
image-20220219161837485

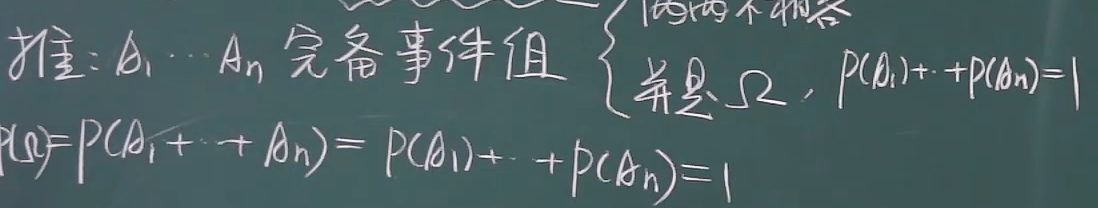
image-20220219162152535

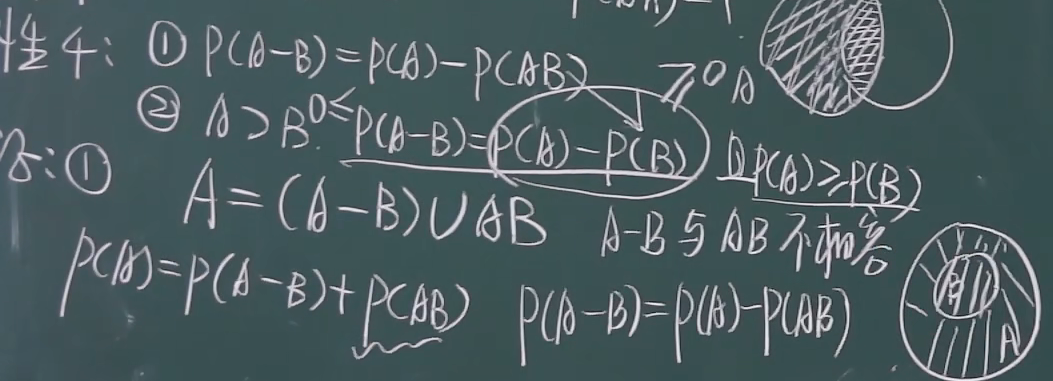
image-20220219162708974

5.加法性质 ！！！

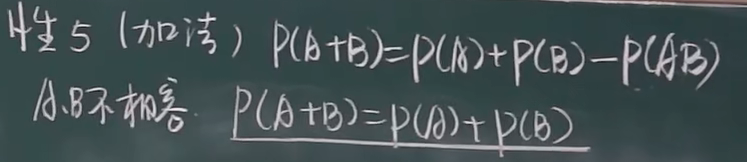
image-20220219163531614

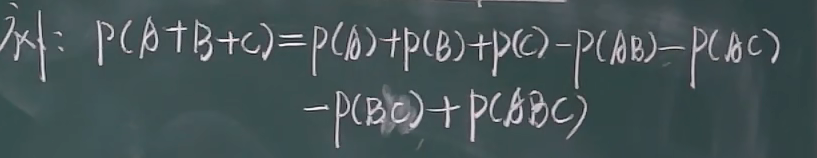
image-20220219163628766

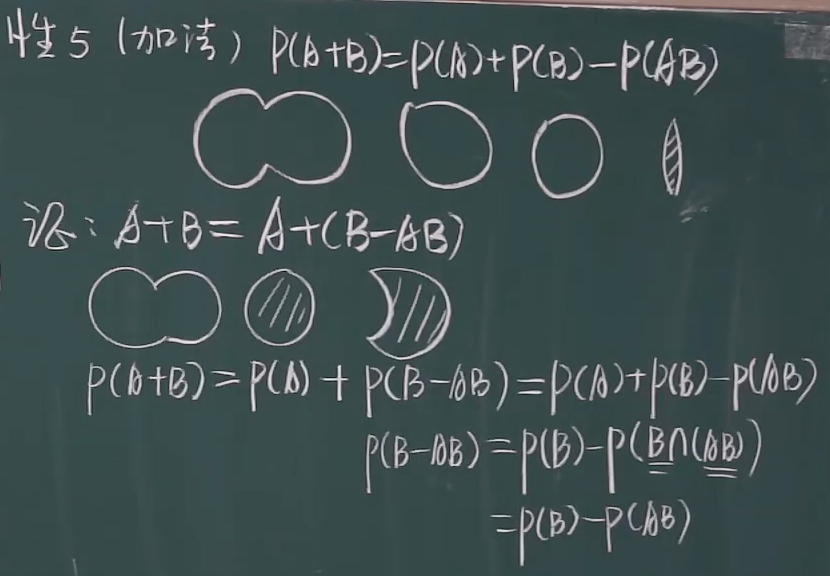
image-20220219163342581

一.三 p(AB) = p(A)p(B|A)

1.3.1 条件概率

image-20220220124659430

image-20220220124709561

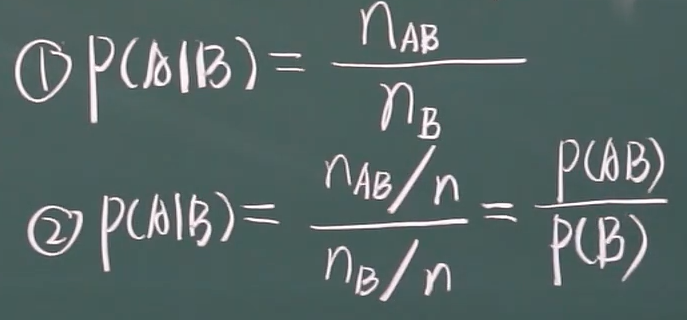
image-20220220124725369

1.3.2 乘法公式

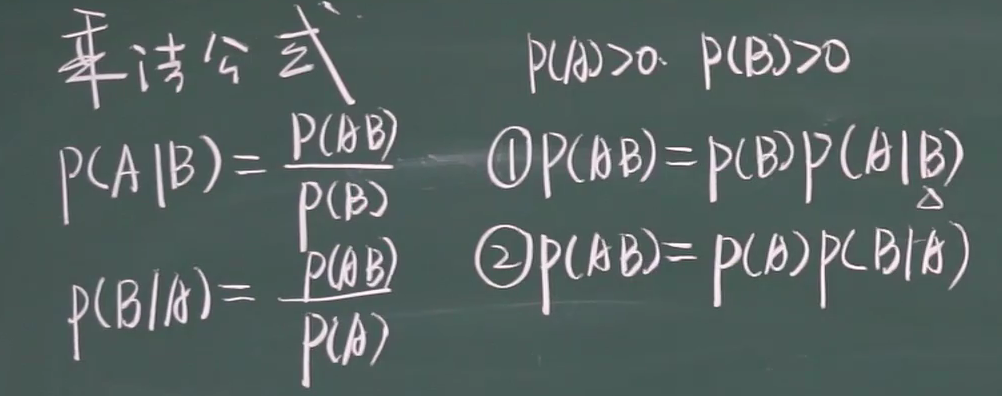
image-20220220130523874

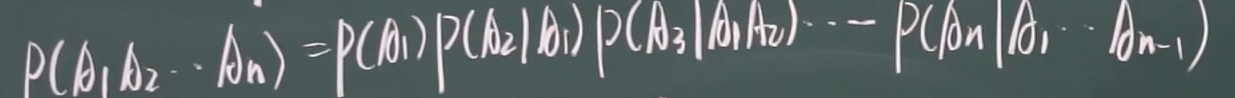
image-20220221102704757

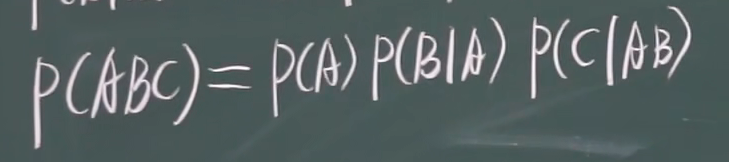
image-20220221102717409

ABC都发生 = A发生 & 在A发生的条件下B发生 & 在AB发生的条件下C发生

一.四 两个公式

1.4.1 全概率公式

分情况讨论用全概率公式

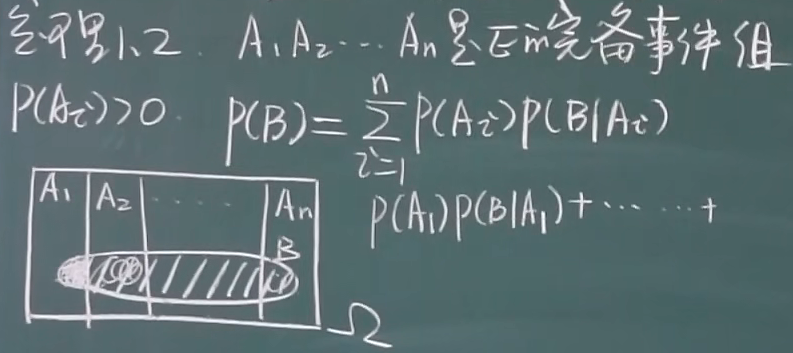
image-20220221135206764

image-20220221142750447

例题1：

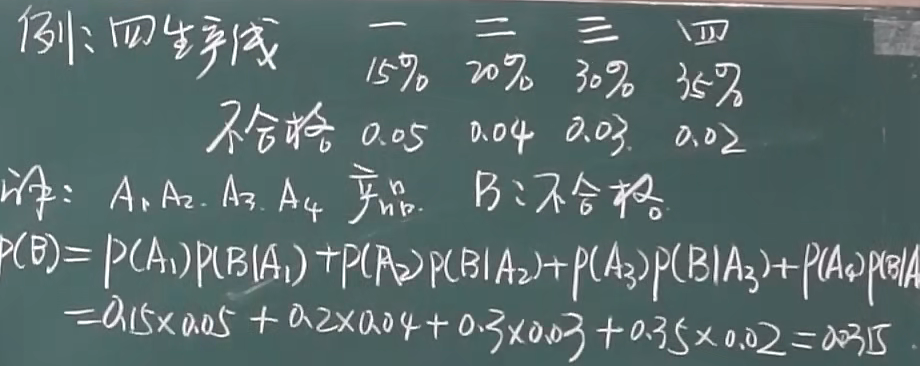
image-20220221135858409

例题2：

image-20220221140351876

例题3：

image-20220221142339908

1.4.2 贝叶斯公式

全概率公式：由因推果

贝叶斯公式：由果推因

image-20220222113201408

先验概率，后验概率

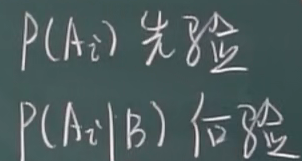
image-20220222113216063

一.五 独立性

1.5.1 事件的独立性

定义

image-20220222120059225

对称性：A对B独立，B也对A独立

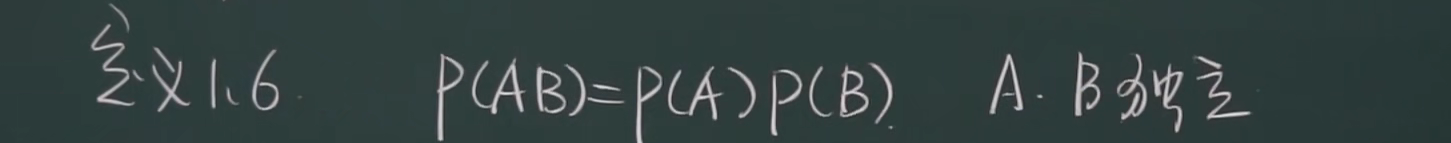
image-20220222120953359

image-20220222142953650

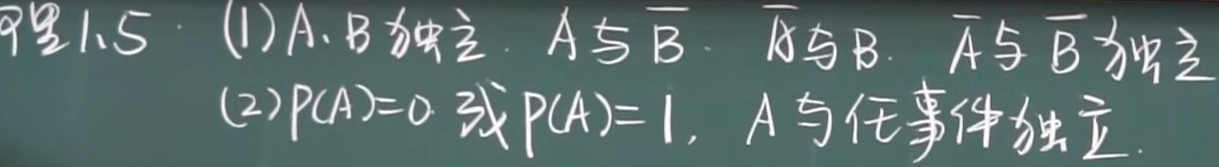
image-20220222143204827

独立和互不相容的区别

事件的独立和事件互不相容两个概念的区别：

1.互不相容考虑的是事件是否能同时发生。A和B互不相容的意思是A发生B就不可能发生。B发生A就不可能发生，也就是说A和B不能同时发生。

2.独立考虑的是两个事件的关联性，一个事件的发生能否影响另一个事件。A和B独立的意思就是，A发生和B发生没有关系，A发生不会影响B发生，A和B也可能同时发生，不过A和B互不影响。

image-20220222150449110

image-20220222220022868

三个事件独立

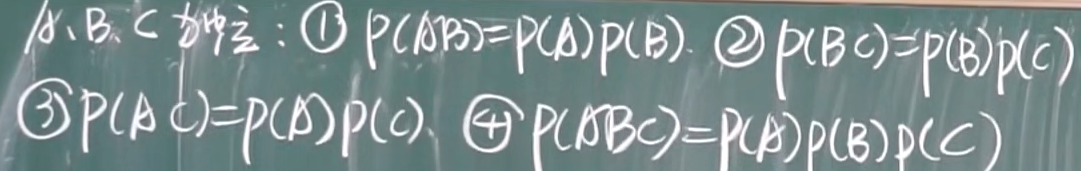
image-20220222220827159

例题

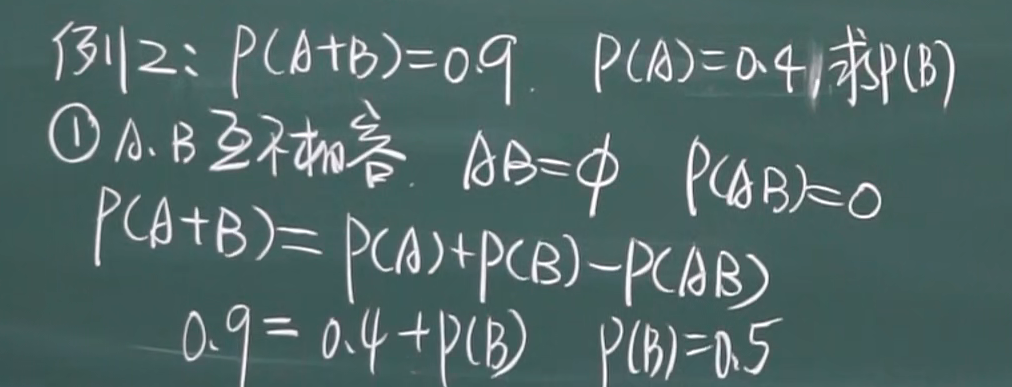
image-20220222221424565

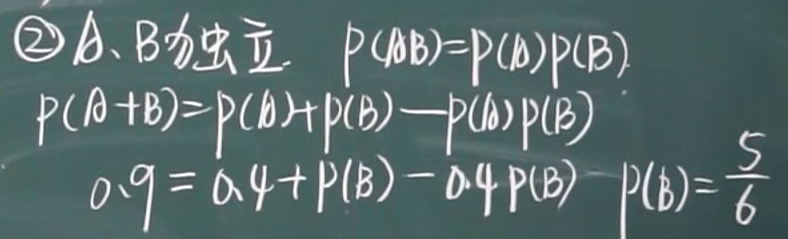
image-20220222221441764

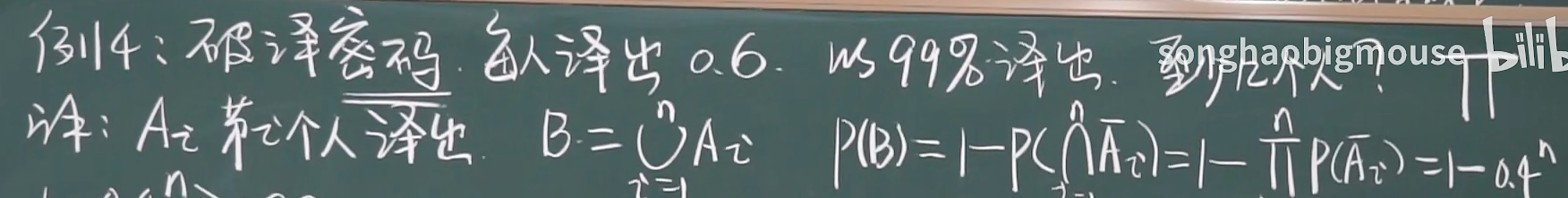
image-20220227210127359

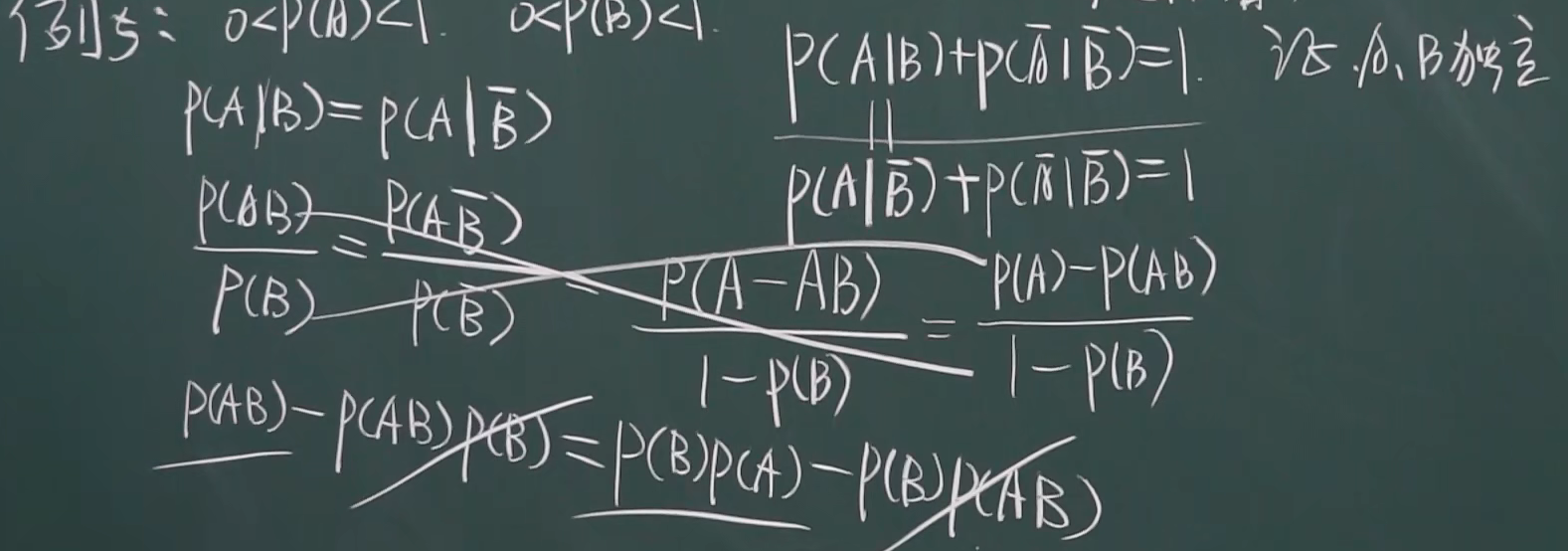
image-20220227210054487

1.5.2 伯努利模型

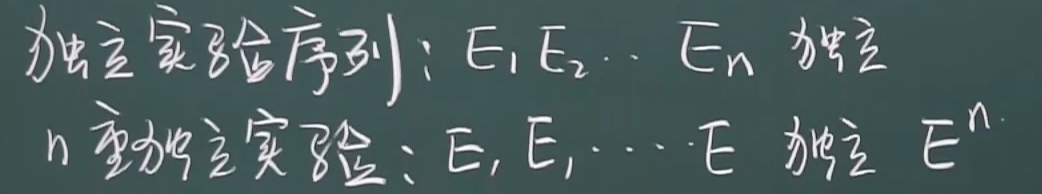
image-20220227213148788

image-20220227213250256

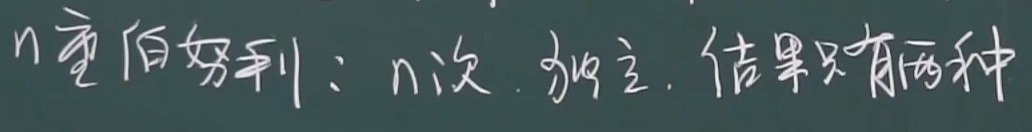
image-20220227213316102

二项概率公式

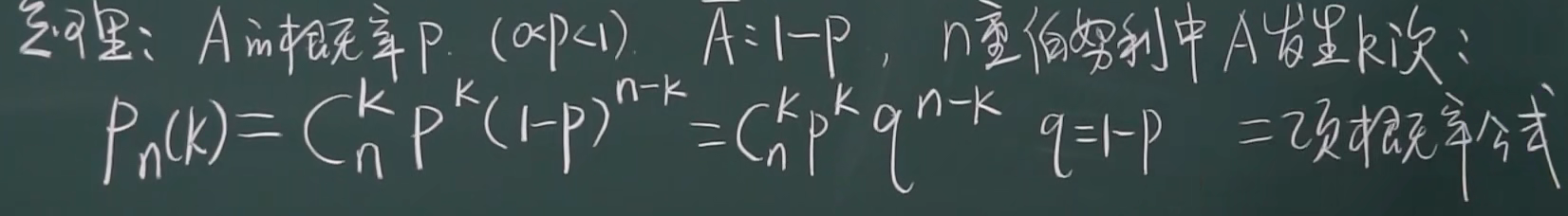
image-20220227213851200

posted @ 2022-02-17 14:00  Cornfield_Chase  阅读(372)  评论(0)    收藏  举报