2020-2021 Summer Petrozavodsk Camp, Day 6: Korean Contest

链接

A	B	C	D	E	F	G	H	I	J	K
\(\color{green}{\texttt{+4}}\)	\(\color{red}{\texttt{+1}}\)		\(\color{gray}{\texttt{+}}\)	\(\color{gray}{\texttt{+}}\)	\(\color{gray}{\texttt{+2}}\)	\(\color{green}{\texttt{+}}\)	\(\color{red}{\texttt{+2}}\)		\(\color{red}{\texttt{+}}\)	\(\color{green}{\texttt{+}}\)

G. Solo Tree Game

E. Observer Game

签到题。

D. Non-Decreasing Subarray Game

显然后手会选 \(L\) 或者 \(R\)。可以发现先手选的位置是单峰的，直接二分往较高的方向走。对于区间不降子区间数量可以直接前后缀和处理一下 \(O(1)\) 查询。

K. Determinant

一个显然的想法是 \(|A-xI|\) 是一个关于 \(x\) 的 \(n\) 次多项式，取 \(n\) 个值插出来就是 \(O(n^4)\) 的，显然过不去。

仔细想一想插出来的多项式满足 \(x_0\) 是特征值时 \(f(x_0)=0\)。然后发现 \(f\) 就是特征多项式。直接用 特征多项式 \(O(n^3)\) 算出即可。

复杂度 \(O(n^3+nq)\)。

A. Mango

大屎题。

先考虑暴力：贪心从 \(M_k\) 从左往右扫，如果扫到 \(M_{k-1}\) 并且 \([l,r]\) 存在一部分在 \(M_{k-1}\) 中，那么向下递归。复杂度 \(O(qnk)\)。

考虑优化。首先特判只有一个 $ 的情况（此时就是 \(t_0^a+s+t_1^a\) 的形式），对于剩下情况，可以发现对于 \(M_i,i>60\) 的部分，只要保留第一个 $ 与其前面的部分即可，因为 \(M_{i-1}\) 长度一定超过 \(10^{18}\)。

这样对于 \(M_{61}\sim M_n\) 部分等价于是 \(t_0^a+M_{60}\)，先特殊处理掉。那么剩下只有 \(60\) 个串，复杂度变成 \(O(qn\log V)\)。

考虑如果询问是 \([1,r]\) 的形式显然直接扫过去复杂度就是正确的。否则对于每个串预处理前缀长度，二分找到需要输出第一个位置，那么每一层只会二分一次。

复杂度 \(O(n\log q\log V)\)。

B. Koosaga's Problem

神仙题。

因为二分图是没有奇环的图，考虑用一种设置边权的方式，要求二分图异或和为 \(0\)，否则不为 \(0\)。

考虑构造一个生成树，对于非树边定义权值 \(2^i\)，并将树边异或上该权值，结论是这样处理之后的总边权异或和符合上述的要求。证明考虑对于每条边的权值分偶环和奇环讨论，偶环异或偶环还是偶环，偶环权值和为 \(0\)，奇环一定会有权值。

容易发现要割边一定不会割权值为 \(0\) 的边，所以求割两条边之后合法的数量等价于求 \(x\oplus y=0\) 的边 \(x,y\) 数量。割一条边和不割边随便判一下就好了。

当然权值 \(2^i\) 显然做不到，其实直接 rand 一个整数即可。

F. Rhythm Game

神必音游，连击的倍率会是负的，而且还是单减的。

考虑 dp，用 \(f_{i,j}\) 表示当前在 \(i\) 敲击了 \(j\) 次的最优分数。显然枚举上一个一直连击的点 \(k\) 就有一个 \(O(n^3)\) 的 dp。

考虑优化。固定 \(j\)，容易发现 \(i\) 维度有决策单调性，即不会出现敲击位置向后，一直连击的起始点反而向前的情况（因为连击越多分数越少），然后就是经典套路，直接分治处理即可。

复杂度 \(O(n^2\log n)\)。

J. Setting Maps

看到 \(100\) 而且不太能 dp，考虑网络流。

首先对于 \(k=1\) 的情况，可以每个点拆点，入点向出点连 \(1\) 边，原图中的边连 \(+\inf\)，实际上是求最小割。

对于 \(k>1\) 的情况，考虑建 \(k\) 层图，每层点之间和上面一样，每层点向下一层对应的出点连 \(+\inf\)，表示这个点被割掉了，不得不到下一层。\(s\) 向 \((0,S)\) 连边，\((x,E)\) 向 \(t\) 连边。

可以发现如果一条路径有少于 \(k\) 个选择的点，那么这条路径一定对应 \(s\) 到 \(t\) 的流量。

但是这可能有一个问题：一个点如果被选择，本质上应该在 \(k\) 层图中都被割掉。不过这没有影响，考虑处理一个点时只需要考虑 \(S\) 到这个点路径中经过选择点最少的那条即可，其余不用考虑，转化到最小割上就是保证有流量的点中层数最小的那个点被割掉即可。

直接跑最小割，复杂度 \(O(n^2k^2m)\)。当然铁定是跑不满的。

H. Stone Catch Game

神仙题。

定义每个黑点的直接控制区域是它往射线的射线经过的点。可以发现如果白点经过这些点，白方必输。

考虑将每个点的射线画出来：

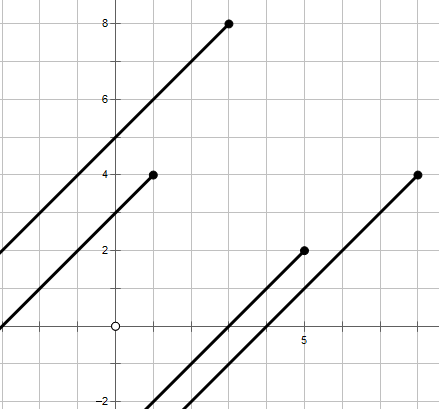
结论：排除一个黑点直接控制白点（\(x=y\)）的情况，如果黑方胜，那么一定存在两个点，使得只保留这两个点仍然黑方胜。

证明显然，因为最后的限制一定只有包含白点的两条黑射线。

不妨把 \(x<y\) 的点与 \(x>y\) 的点分成两个集合，容易发现最后选出的点一定是两个集合中各选一个。

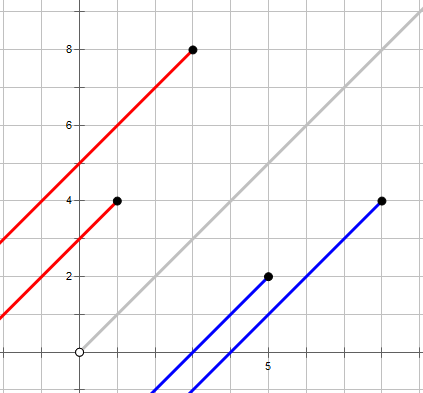
接下来考虑怎样的两个点是合法的。贪心地想，左集合（红色射线）一定只会往下走，右集合（蓝色射线）一定只会往左走。

容易发现，如果最后两个点之间的距离是 \((2,2)\)，即：

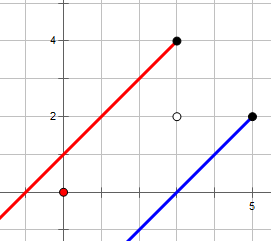
容易发现此时白点永远出不去。设左边的点为 \((x_1,y_1)\)，右边的点为 \((x_2,y_2)\)，那么要求是 \(y_1+x_2\leq \max(|y_1-y_2|-2,0)+\max(|x_2-x_1|-2,0)\)。

然而这样并不是全部情况。因为我们钦定的一点是 \(y_1>y_2,x_1< x_2\)，然而事实上可能发生这种情况：

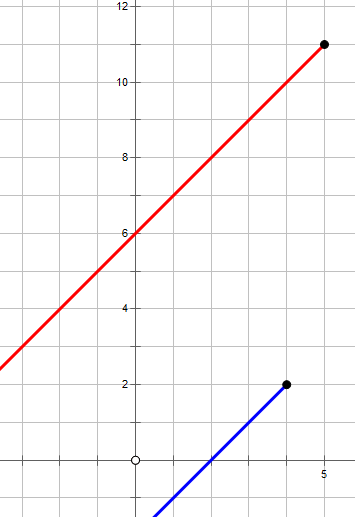
但是贪心地想，我们无论如何不会把红线左移，那么可以认为是 \(x_1=x_2\)。\(y\) 坐标同理。

所以最终的式子是：\(y_1+x_2\leq \max(y_1-y_2-2,0)+\max(x_2-x_1-2,0)\)。

考虑对左集合和右集合建单调栈，这样每个集合中 \((x,y)\) 均递增。然后枚举 \((x_1,y_1)\)，分讨 \(x_2,y_2\) 在两个括号内的情况。对应在单调栈上是四个区间，直接二分/双指针即可。

复杂度 \(O(n\log n)\)。事实上由于数据极水，直接 \(O(n^2)\) 暴力扫过去就可以通过。