AtCoder Grand Contest 035

链接

C. Skolem XOR Tree

人类智慧题。

考虑一个性质，对于一个偶数 \(i\) 一定有 \(i\oplus 1=i+1\)。

考虑将 \(1\) 作为根，对于 \(i\in[2,n]\)，将其放入左子树，否则放入右子树。

考虑对于偶数 \(i\)，只需要让它经过 \(i+1,1\) 即可。对于奇数则经过 \(i-1,1\)。

故对于偶数 \(i\) 直接连边 \(i\rightarrow i+1\rightarrow 1\rightarrow i+n\rightarrow i+n+1\)。

这样还剩下一个 \(n+1\)，直接挂到任意叶子上即可。

最后可能还剩下没有配对的两个数字，特殊处理一下一定能挂到某两个叶子上。

复杂度 \(O(n)\)。

#include<iostream>
#include<cstdio>
#include<cstring>
#define N 100010
using namespace std;
int main()
{
    int n,m=0;
    scanf("%d",&n);m=n&(-n);
    if(m==n){puts("No");return 0;}
    puts("Yes");
    for(int i=2;i<n;i+=2) printf("1 %d\n1 %d\n%d %d\n%d %d\n",i,i+n+1,i,i+1,i+n,i+n+1);
    if(!(n&1)) printf("%d %d\n%d %d\n",n,n+m+1,n*2,n-m);
    printf("%d 3\n",n+1);
    return 0;
}

D. Add and Remove

考虑对于一个位置 \(i\)，其在最后的答案中一定会出现若干次，不妨记作 \(x_i\)。

考虑一个区间 \([l,r]\) 的贡献。不妨假设其左端会在原序列贡献 \(v_l\) 次，右端会贡献 \(v_r\) 次，那么我们可以 dp 求出 \(f(l,r,v_l,v_r)\)。

复杂度 \(O(n^22^n)\)。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<map>
#define ll long long
#define P pair<ll,ll>
#define MP make_pair
#define N 18
using namespace std;
int a[N];
map<P,ll>p[N][N];
ll dfs(int l,int r,ll vl,ll vr)
{
    if(l>=r-1) return 0;
    if(p[l][r].count(MP(vl,vr))) return p[l][r][MP(vl,vr)];
    ll &res=p[l][r][MP(vl,vr)];res=1e16;
    for(int j=l+1;j<r;j++) res=min(res,dfs(l,j,vl,vl+vr)+dfs(j,r,vl+vr,vr)+a[j]*(vl+vr));
    return res;
}
int main()
{
    int n;
    scanf("%d",&n);
    for(int i=1;i<=n;i++) scanf("%d",&a[i]);
    printf("%lld\n",dfs(1,n,1,1)+a[1]+a[n]);
    return 0;
}

E. Develop

首先考虑如何计数。考虑如果存在变换 \(x\rightarrow y\)，而且 \(x,y\) 都存在，那么必须钦定 \(y\) 先决定是否变换，然后 \(x\) 再决定是否变换为 \(y\)。

如果把删除一个点看成染色，对于所有变换构成 DAG 的情况，必须有按照拓扑序进行操作。换句话说所有删除的点组成的导出子图不能有环。

考虑分类讨论，如果 \(2|k\) 代表奇偶分类后不同类点间不存在边。这个直接 dp 就好了。

考虑 \(2\nmid k\) 可以发现一定构成这样一张图：

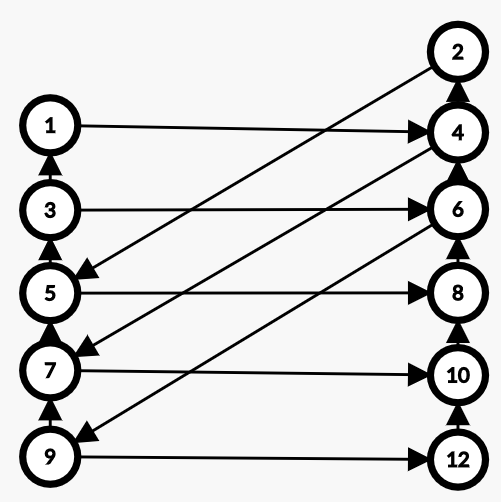
令 \(f_{i,j,k}\) 表示当前在从下往上第 \(i\) 行，左边往下 \(j\) 个删除点，右边往上 \(k\) 个删除点的方案数。

直接 dp，复杂度 \(O(n^3)\)。

#include<iostream>
#include<cstdio>
#include<cstring>
#define N 310
using namespace std;
int n,m,mod;
int f[N][N][N];
int main()
{
    scanf("%d%d%d",&n,&m,&mod);
    if(m%2==0)
    {
        static int f[N][N];
        memset(f,0,sizeof(f));
        f[0][0]=1;
        for(int i=1;i<=n;i++)
            for(int j=0;j<=m/2;j++) f[i][0]=(f[i][0]+f[i-1][j])%mod,f[i][j+1]=(f[i][j+1],f[i-1][j])%mod;
        int r1=0,r2=0;
        for(int i=0;i<=m/2;i++) r1=(r1+f[n/2][i])%mod,r2=(r2+f[(n+1)/2][i])%mod;
        printf("%d\n",1ll*r1*r2%mod);
        return 0;
    }
    f[0][0][0]=1;
    int p=(n+m)/2*2;
    for(int i=0;i<p;i+=2)
        for(int j=0;j<=n;j++)
            for(int k=0;k<=m+1;k++)
            {
                (f[i+2][0][0]+=f[i][j][k])%=mod;
                if(i<=n-2) (f[i+2][j+1][0]+=f[i][j][k])%=mod;
                if(i>=m-1) (f[i+2][0][k?k+1:0]+=f[i][j][k])%=mod;
                if(i<=n-2 && i>=m-1) (f[i+2][j+1][max(k+1,j+2)]+=f[i][j][k])%=mod;
            }
    int ans=0;
    for(int j=0;j<=n;j++)
        for(int k=0;k<=m+1;k++) ans=(ans+f[p][j][k])%mod;
    printf("%d\n",ans);
    return 0;
}

F. Two Histograms

操作总数显然是 \((n+1)^m(m+1)^n\)

考虑什么情况下会计重：

01      .|      .|
11  =>  --  or  -|

可以证明的是，只有这种相交的情况会计重，其余情况均没有影响。

考虑 \(f_i\) 表示至少 \(i\) 个相交的情况，确定行列的方案数是 \(\binom{n}{i}\binom{m}{i}\)，可以发现任意一行或一列只会出现至多一次，故方案数是 \(i!\binom{n}{i}\binom{m}{i}(n+1)^{m-i}(m+1)^{n-i}\)。

直接容斥，答案即 \(\sum(-1)^if_i\)。

#include<iostream>
#include<cstdio>
#include<cstring>
#define N 1000010
#define mod 998244353
using namespace std;
int fac[N],inv[N];
int ksm(int a,int b=mod-2)
{
    int r=1;
    for(;b;b>>=1)
    {
        if(b&1) r=1ll*r*a%mod;
        a=1ll*a*a%mod;
    }
    return r;
}
int C(int a,int b){return a<b?0:1ll*fac[a]*inv[b]%mod*inv[a-b]%mod;}
void init(int n=N-10)
{
    fac[0]=1;
    for(int i=1;i<=n;i++) fac[i]=1ll*fac[i-1]*i%mod;
    inv[n]=ksm(fac[n]);
    for(int i=n-1;i>=0;i--) inv[i]=1ll*inv[i+1]*(i+1)%mod;
}
int main()
{
    int n,m;
    scanf("%d%d",&n,&m);
    init();
    if(n>m) swap(n,m);
    int ans=0;
    for(int i=0;i<=n;i++) ans=(ans+(i&1?mod-1ll:1ll)*C(n,i)%mod*C(m,i)%mod*fac[i]%mod*ksm(n+1,m-i)%mod*ksm(m+1,n-i))%mod;
    printf("%d\n",ans);
    return 0;
}