带花树学习笔记

带花树学习笔记

大部分内容参考 这篇博客 和 2015集训队论文。

关于匹配

定义翻转一条路径指的是将路径中所有匹配边变为非匹配边，非匹配边变为匹配边。

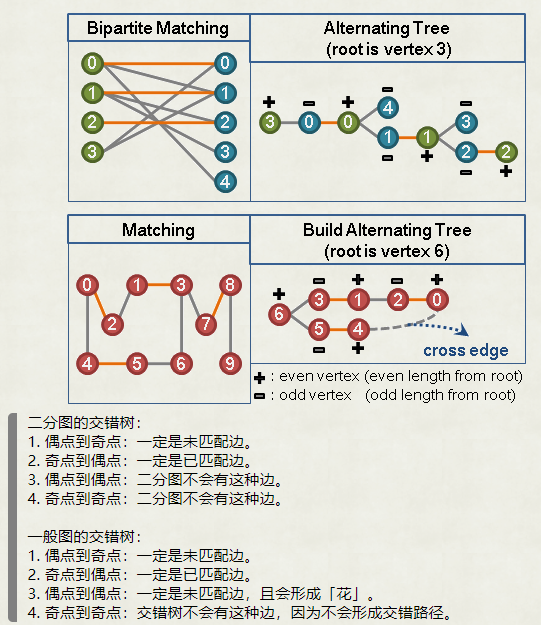
定义一种路径是交错路径 (Alternating Path) 当且仅当路径是由匹配边和非匹配边交错产生。交错环 (Alternating Cycle) 同理。举例：

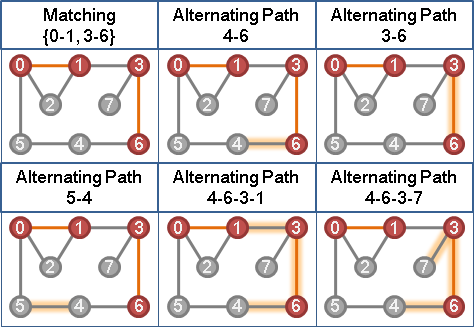
可以发现的一个性质是：交错环的所有边翻转后不影响匹配个数。

定义一种路径是扩充路径 (Augmenting Path) 当且仅当它是一条交错路径且起始点和终止点都没有匹配。举例：

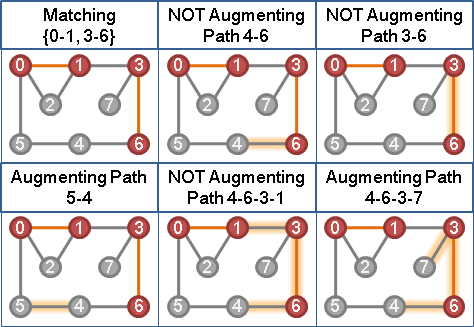
可以发现的一点是，如果存在扩充路径，那么翻转扩充路径可以使匹配 \(+1\)。

显然如果存在扩充路径，那么一定可以使匹配 \(+1\)。那么是不是不存在扩充路径就对应最大匹配呢？事实上这是可以证明的，只需要对非匹配点与非扩充路径的情况分类讨论即可。

这样不断找到扩充路径，实际上就可以得到一个最大匹配。

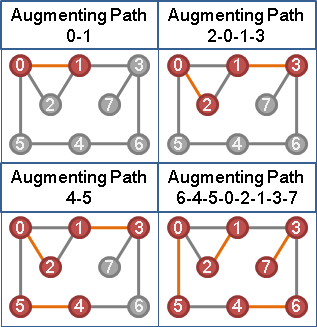
定义交错树 (Augmenting Tree) 是以一个未匹配点作为树根，所有从树根出发的路径都是交错路径的树。

当然路径总数会很大，事实上对于每条路径，我们只需要保留在任意一颗子树中即可。

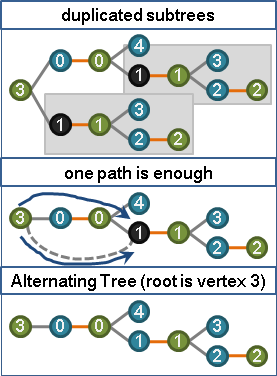
可以证明这样总是正确的。

关于二分图匹配

如果给定一张二分图，如何求出最大匹配。

二分图匹配的经典做法有匈牙利或者网络流，后者可以做到 \(O(m\sqrt n)\) 的复杂度。

考虑二分图匹配为什么是对的。对于匈牙利算法来说，它的实质是找到一个未匹配点，然后遍历了以它为根的交错树，尝试搜索一条扩充路径更新。

网络流算法则更加直接，利用二分图的性质钦定每条边的方向向右，钦定向左的边表示匹配边，向右的边表示非匹配边。直接套用网络流的反向弧来找到扩充路径。可以发现一条扩充路径恰好对应一次增流。

关于一般图匹配

如果这是一张二分图，那么上述问题可以通过匈牙利或者网络流算法做到非常好的复杂度。但如果这张图没有任何性质，由于网络流算法实际是利用二分图将无向边改成有向边，处理增广路径，这里就不大行了。

但是能不能大力跑匈牙利处理呢。即每次查询一个点，如果它被匹配了就尝试更换它匹配的点的匹配边。但这样是有反例的：如果交错路径经过了某个奇环，那么翻转后会使得某一个点存在两个匹配。

但是这个问题只会在奇环的时候出现。

可以发现如果存在这样的“花” (blossom)，那么我们一定是从“花托” (base) 的位置进来的。可以证明在这种情况下，任何条经过花的扩充路径等价于缩完“花”之后的一条扩充路径。

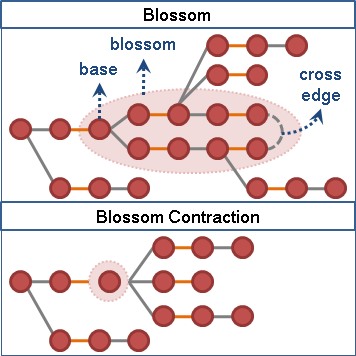
注意这里的“花”只对当前扩充路径有效，所以当次扩充完需要重置。

这样处理之后剩下的其实就是一张二分图，直接按类似于匈牙利的方式处理一下就行了。

为了保证复杂度正确，使用 BFS 寻找扩充路径，如果遇到奇环就反复条父亲来找到“花托”。这样在一次扩充的过程中，一条边只会被访问一次，故复杂度为 \(O(nm\alpha(n))\)。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#include<vector>
#define N 20010
using namespace std;
int n,m;
vector<int>g[N];
namespace flower_tree{
    queue<int>q;
    int col[N],f[N];
    int find(int x){return f[x]==x?f[x]:(f[x]=find(f[x]));}
    int pre[N],lik[N];//pre:增广路 , lik:匹配
    int T,vis[N];
    int lca(int x,int y)
    {
        for(x=find(x),y=find(y),++T;vis[x]!=T;)
        {
            vis[x]=T;
            x=find(pre[lik[x]]);
            if(y) swap(x,y);
        }
        return x;
    }
    void flower(int x,int y,int v)
    {
        for(;find(x)!=v;x=pre[y])
        {
            pre[x]=y;y=lik[x];
            if(col[y]==2) col[y]=1,q.push(y);
            if(f[x]==x) f[x]=v;if(f[y]==y) f[y]=v;
        }
    }
    void clear(int n)
    {
        while(!q.empty()) q.pop();
        for(int i=1;i<=n;i++) f[i]=i,pre[i]=col[i]=0;
    }
    bool dfs(int s,int n)
    {
        clear(n);
        col[s]=1;q.push(s);
        while(!q.empty())
        {
            int u=q.front();q.pop();
            for(int v:g[u])
            if(find(u)!=find(v) && col[v]!=2)
            {
                if(col[v])
                {
                    int w=lca(u,v);
                    // if(w==0) throw;
                    flower(u,v,w);flower(v,u,w);
                    continue;
                }
                col[v]=2;pre[v]=u;
                if(lik[v]) col[lik[v]]=1,q.push(lik[v]);
                else
                {
                    for(int x=v,y=lik[pre[x]];x;x=y,y=lik[pre[x]])
                        lik[x]=pre[x],lik[pre[x]]=x;
                    return true;
                }
            }
        }
        return false;
    }
}
using flower_tree::dfs;
using flower_tree::lik;
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++)
    {
        int u,v;
        scanf("%d%d",&u,&v);
        g[u].push_back(v);g[v].push_back(u);
    }
    int ans=0;
    for(int i=1;i<=n;i++)
    if(!lik[i]) ans+=dfs(i,n);
    printf("%d\n",ans);
    for(int i=1;i<=n;i++) printf("%d ",lik[i]);
    return 0;
}