0阶段-第四日-tarjan算法在图的连同性中的运用。

人不摸，就会死。
第四日，tarjan算法在图的连同性中的运用。

自上至下对应内容为：
全部基于tarjan算法实现：
1、求强连通分量，缩点，拓扑排序
2、割点
3、缩点
4、添边使图强连通，缩点
5、无向连通图转强连通图（规定边方向），桥 6、同3 7、类似于4 8-10、裸2-SAT
所学整理如下：
0、前置
设无向连通图为G，构造形成DFS树为T，规定边方向形成有向图为G。设T中某一条树边为uv，孩子为v，父亲为u，以该孩子为根的子树集合为U，T中所有节点的公共祖先为集合为S，S删去u的的集合为S。
1、桥、连通无向图转强连通图
1、当然是在无向连通图G中讨论
2、把图构造成任意一颗一颗dfs树T，两者当然是等价的。
3、回边不可能是桥，桥只能树边，若有重边或自环，则它们为回边。
4、每一个回边对应树上的一个简单路径，可视该简单路径中的每一条树边被回边覆盖。纵观整张图，被覆盖的树边和回边不可能是桥，没有被覆盖的树边必定为桥（形象点就是没有回边从它头上跨过去）。被覆盖的边uv，意味者v可以不经过uv，从经过回边可以回到S中。
5、没覆盖的边uv就是桥，也就是说v不通过桥，就无法回到S中。
6、容易证出，对于v，如果U中没有没有回边连接S，那么uv就是桥。 7、如果有回边连接S，那么uv必不是桥。
8、这样就能通过low传递U中回边指向的时间戳，来判断6、7。
8、给树边uv规定方向：u->v；给回边规定方向：指向祖先。这样就构造除了G。
9、如果G中没有有桥，那么对于v，总能通过U中的一条回边回到S，也就意味这G中，该从u到v后，v总能通过规定方向的回边回到它的祖先。也就是说除了G中根节点外的任何一个节点都能能往树根方向回溯，最终辗转回到根节点，而根节点又可以到图上的每一个节点，所以该图强连通。
10、如果有桥，那必然非强连通。
如图（源自OI WIIK）

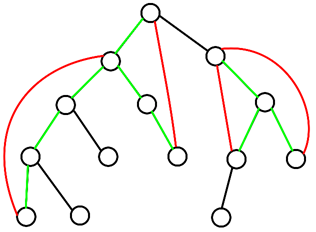
2、 割点
0、先不考虑树根
1、割点，删除去该点后，无向连通图被划分为两个连通块。
2、等价于v通过U中回边最多能回到u，等价于v通过U无法回到S。
3、桥是做多回到S，而割点是S。
4、所以判断的时候加一个等于就好。
5、特例：根。对于根的所有孩子，S*是空集，也就是说根的孩子只要有两个或以上，那必然是割点。而其它节点由于必有父节点，如果有孩子一个以上，那么满足条件就是割点。所以根要特判。
3、有向图填边构造强连通图的方法
max(出度为0的缩点数，入读为0的缩点数) 。图本身就是强连通需要特判。
**4、2-SAT **
通俗的说，就是命题逻辑题。就是给你一个一些限制条件，要你找成真赋值。例如：
限制条件：(a|b)&!(a&b)&(a->c)
要求就是判断成真赋值是否存在。
首先利用基本等式转化一下：
a|b<=>(!a->b)&(!b->a)
!(a&b)<=>!a|!b<=>(a->!b)&(b->!a)
a->c<=>(a->c)&(!c->!a)
即：
(a|b)&!(a&b)&(a->c)<=>(!a->b)&(!b->a)&(a->!b)&(b->!a)&(a->c)&(!c->!a)
限制条件就变成了后者。
把它化成一张图：

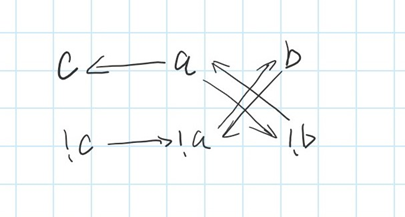
至于为什么是p|q<=>(!p->q)&(!q->p)而不是p|q<=>(!p->q)，这样在图中对应只连上一条边。我想是为了保证通过图构造的解的真确性。否则约束不够强得不出正确答案。
图中的边当然还是蕴含连接词，我们只是把它画成了图。
我们根据图来寻找成真赋值：
1、如果强连通分量中，的所有命题真值相同，由假言推理很容易看出。
2、由此显然，如果强连通分量中包含某一命题q,同时又包含命题!q，那么不存在一个成真赋值。
3、对任意p，都和!p不在一个强连通分量中，那么成真赋值一定存在，没有证明。
4、在用tarjan算法找强连通分量的过程中，同时给每个强连通分量打上拓扑排序的逆序，用scc[]记录这个逆序。如果谁的scc小就给谁赋值为真(如果打上的正序，那就大的为真)。可以保证这样的方式构造的解总是存在的.例如scc[!q]<scc[q],那么就另!q=1,q=0。对每个命题这么操作后我们就可以得到一个满足限制条件的解。
5、做这类题目的关键就是把题目转化为逻辑命题进行分析。