数据结构-一维树状数组维护区间和

一维树状数组

有两张图觉得很好用，转载过来了：
原地址 https://blog.csdn.net/bestsort/article/details/80796531

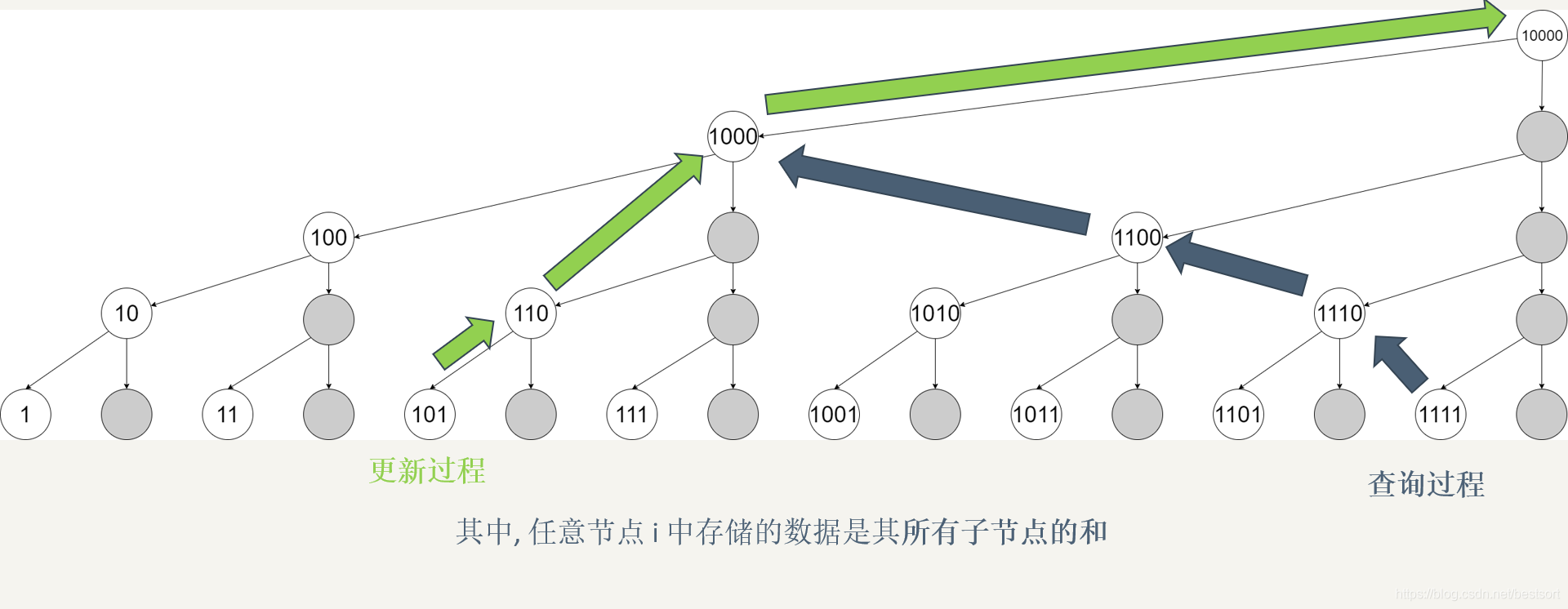
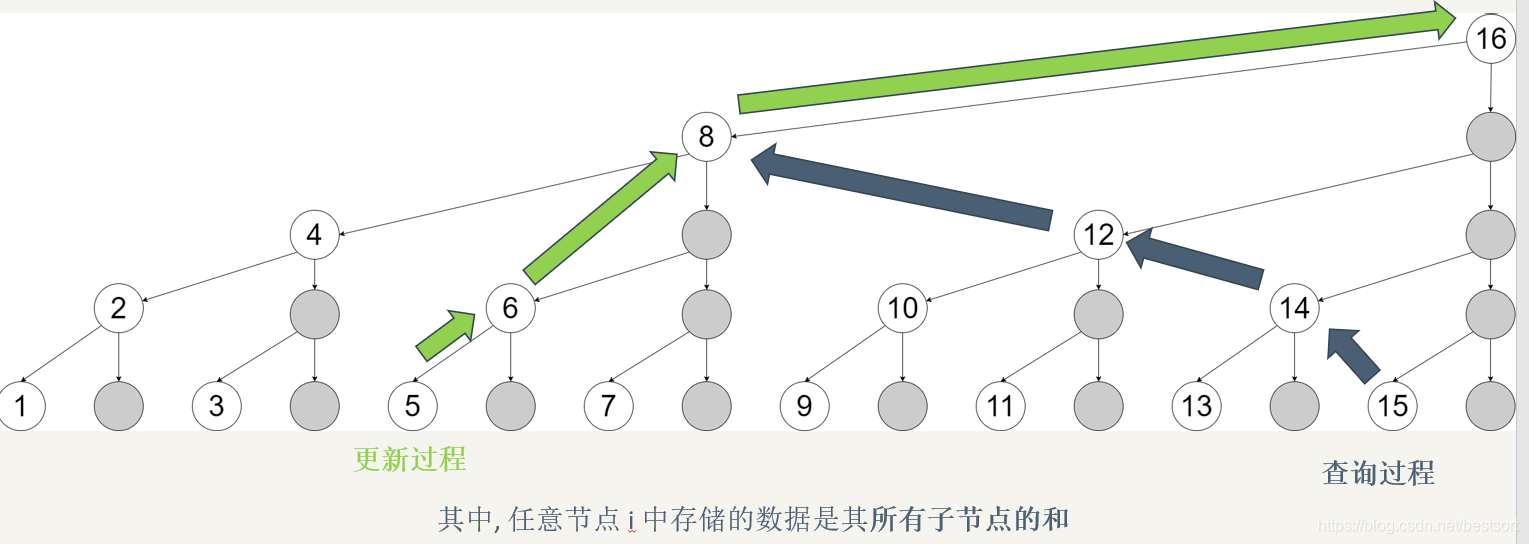
对于原数组\(arr\)：
单点更新，区间查询
均为\(O(logn)\)

#include<cstdio>
#include<iostream>
using namespace std;

typedef long long ll;

int n,m,arr[500010],c[500010];

inline int lowbit(int x)//求二进制低位，即lowbit
{
    return x&-x;
}

void add(int i,int k)//单点更新
{
    while(i<=n)
    {
        c[i]+=k;
        i+=lowbit(i);
    }
}

int getsum(int i)//求原数组前i项和，区间查询再求差就好
{
    int sum=0;
    while(i)
    {
        sum+=c[i];
        i-=lowbit(i);
    }
    return sum;
}


int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;++i)
    {
        scanf("%d",arr+i);
        add(i,arr[i]);//构造树状数组
        return 0;
    }

区间更新，单点查询
构造差分数组d,规定\(d[i]=arr[i]-arr[i-1](i>=1\&\&i<=n)\)，对\(d[i]\)构造树状数组，这样单点查询可以通过求和实现，区间更新可以通过树状数组的单点更新实现，时间复杂度为\(O(logn)\)。

void range_add(int lef, int rig, int x)//区间更新
{
    add(lef,k);
    add(rig+1,-k);
}

int getnum(int i)//单点查询
{
    return getsum(k);
}

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;++i)
    {
        scanf("%d",arr+i);
        d[i]=arr[i]-arr[i-1];
        add(i,d[i]);//构造
    }
}

区间查询
区间查询功能由差分树状数组拓展而来。我们可以原数组的差分数组来求出原数组的前缀和，时间复杂度为\(O(n)\)，其公式可化为\((x+1)∑^x_{i=1}d_i-∑^x_{i=1}i*d_i\)。这样只要再构造数组i*d[i]的树状数组就好,定义为f。
只需更改一下add函数和getsum函数即可

void add(int i,int k)
{
    int x=i;
    while(i<=n)
    {
        c[i]+=k;
        f[i]+=k*x;//同时更新f
        i+=lowbit(i);
    }
}

int getsum(int i)//区间查询求差就好
{
    int res=0,x=i;
    while(i)
    {
        res+=(x+1)*c[i]-f[i];//对应公式
        i-=lowbit(i);
    }
    return res;
}

其余地方套用前一个二分树状数组的代码就好。

最后

写了自己想要的，由于差分的区间查询本人有些许烦躁，个别地方可能马虎以至于出错，请包涵。