[EGOI 2025] Laser Strike / 激光突击 题解
第一道通信!!!
[EGOI 2025] Laser Strike / 激光突击
\((n-1) bit\)
对于一条连接叶子的边 \((u,v)\),我们用 \(1 bit\) 表示他的特征值,如果其中的叶子是 \(\min(u,v)\) 则特征值为 \(1\),否则为 \(0\)。
直接用长度为 \(n-1\) 的字符串表示每条边的特征值即可。
菊花
这是简单的,先用 \(1 bit\) 表示第一条边的特征值,那么不用被删的点就是根,对于之后的边只需要保留上一条边没有被删的点即可。于是我们可以总结出一个策略:
策略一:如果当前边与上一条边有公共点,那么保留公共点,删除另一个点。
链
只考虑链的话也是简单的,从左往右删,同样只需要知道第一条边的特征值,之后每次删除上一条边出现过的点即可。
但是这个策略和策略一完全矛盾,考虑换个思路。我们钦定这条链的中点为根(如果链上有偶数个点,那么中点在一条边上),交替删除左链和右链的叶子,我们先用 \(2 bit\) 表示开头删除的两条边的特征值,对于之后的边,如果满足策略一就遵循策略一,否则:
策略二:如果当前边的某个点在之前出现过,且不是在上一条边出现的,那么删除这个点。
举个例子,以偶数个点为例,在删到只剩两个点之前会一直遵循策略二,显然合法,对于最后两个点:
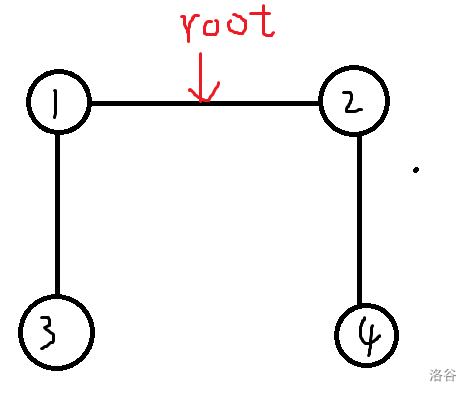
假如在上图中先按顺序删除了 \(3,4\) 之后,还剩下 \((1,2)\) 这条边,由于上一条边是 \((2,4)\) 所以会遵循策略一,删除 \(1\) 号点。
如果是奇数个点的情况,不难验证我们最后会恰好剩下钦定的根节点。
但是现在我们多用了 \(1 bit\),考虑优化,假设开头两条边是 \((a,b),(c,d)\) 我们需要根据他们的某种关系在只知道一条边的特征值的情况下就能推出另一条边的特征值。
一种比较简单的方法是,设计两条边的某种偏序关系,那么如果 \((a,b),(c,d)\) 的特征值一样,就把大的那条边放在前面,否则把小的那条边放在前面,这样我们在得到第二条边时只需要根据他和第一条边的大小关系就能知道他的特征值是啥了。
你可以把这个偏序关系设成你喜欢的任何类型,只需要保证他是确定且严格的就可以了,比如比较一条边构成的无序二元组的字典序。
正解
首先需要明确的是,我们唯一能提供的 \(1bit\) 一定是给出第一条边的特征值,否则 Kathrin 将啥都不知道。
既然我们考虑过链的情况了,那么对于一般树一种经典的思路就是拉出直径,在后面我们会说明选直径的用处。
同样以直径的中点为根,注意如果直径有偶数个点那么会有两个深度为 \(1\) 的点。
我们遇到的第一个问题是,树上可能会有好多完全不相干的叶子,而我们只能提供其中一个叶子的信息,但不妨先假设我们能通过魔法直接得到一条叶边的特征值。
我们先取出所有点 \(u\) 满足 \(u\) 的每个儿子都是叶子,然后使用魔法得到其中某条边的特征值,删掉他,之后按照菊花的思路一直用策略一直到把所有儿子都删光。
接下来我们按照深度从大往小一层层删点,假设当前删第 \(d\) 层,考虑第 \(d-1\) 层的某个点 \(u\),他的儿子现在肯定全都是叶子了,有些一开始就是叶子,有些后来才变成叶子,由于我们已经提前把只有叶子儿子的点处理了,所以他必定有一个儿子 \(v\) 是后来才变成叶子的,也就是说 \(v\) 曾经在某条被删的边出现过,那么就可以用策略二把 \(v\) 删掉,之后就可以一直用策略一把他的其他儿子全都删掉。
注意:如果这个选择的 \(v\) 是第 \(d\) 层第一个被删的点,那么他不能是第 \(d+1\) 层最后删掉的点的父亲,否则在考虑 \((u,v)\) 这条边时,Kathrin 会错误地使用策略一导致把 \(u\) 给删了。不过由于我们在一开始选择了直径中点为根,所以此时第 \(d\) 层至少有两个点,我们一定能选出某个合法的 \(v\)。
好了,现在我们只需要解决魔法的事了,我们取出所有需要知道特征值的叶边 \((u_i,v_i)\),根据链最后部分的思路,我们需要把他们按照某种顺序排列,使得如果 \((u_{i+1},v_{i+1})<(u_i,v_i)\) 则他们的特征值相同,否则不同,这样我们只需要知道第一条边的特征值就好了。实现这个顺序也是简单的,只需要把他们先从小到大排好序,然后 reverse 所有极长特征值相同的段即可。
Kathrin 想要判断一条边是否是需要使用魔法的叶边只需要判断这条边的两个点是否都没有出现过即可。
code
Kathrin 只需要按照策略无脑执行就可以了,但是 Ann 要考虑的就很多了......
#include<bits/stdc++.h>
#define Debug puts("-------------------------")
#define eb emplace_back
#define PII pair<int,int>
#define fi first
#define se second
#define mk make_pair
using namespace std;
const int N=1e3+5;
int OP,n;
namespace Ann{
int p,q,dep[N],fa[N],mxdep,deg[N],lst_del;
vector<int> G[N],vec[N],ans;
bool appear[N],del[N]; //在之前是否出现过;是否被删掉了
char begin_op;
int find_kfa(int x,int k){ while(k) x=fa[x],k--; return x; }
void dfs0(int u,int f,int &rt){
dep[u]=dep[f]+1;
if(!rt||dep[u]>dep[rt]) rt=u;
fa[u]=f;
for(int v:G[u]) if(v!=f) dfs0(v,u,rt);
}
void dfs1(int u,int f,int d){
vec[d].eb(u),fa[u]=f,dep[u]=d,mxdep=max(mxdep,dep[u]);
for(int v:G[u]) if(v!=f) dfs1(v,u,d+1),deg[u]++;
}
int op(int u,int son){ return son<u; }
void remove(int u){
if((int)ans.size()==n-1) return;
// if(del[u]){
// cerr<<"Wrong!!!the node "<<u<<" is already remove"<<endl;
// exit(0);
// }
del[u]=appear[u]=true,lst_del=u;
ans.eb(u);
}
void clear_leaf(int u){ //删除 u 的所有儿子
if(!u) return;
appear[u]=true;
for(int v:G[u]) if(fa[v]==u&&!del[v]) remove(v);
deg[u]=0;
}
void solve_leaf(){ //删除树上所有一开始的叶子
vector<PII> leaf;
for(int u=1;u<=n;u++){
if(!deg[u]) continue;
bool flag=true;
int son=-1;
for(int v:G[u]) if(fa[v]==u){
if(deg[v]){ flag=false; break; }
else son=v;
}
if(flag) leaf.eb(u,son);
}
sort(leaf.begin(),leaf.end(),[&](PII x,PII y){ return mk(min(x.fi,x.se),max(x.fi,x.se))<mk(min(y.fi,y.se),max(y.fi,y.se)); });
int siz=leaf.size();
for(int l=0,r;l<siz;l=r+1){
int opt=op(leaf[l].fi,leaf[l].se);
for(r=l;r<siz;r++) if(op(leaf[r].fi,leaf[r].se)!=opt) break;
r--;
if(l==0) begin_op=opt+'0';
for(int i=r;i>=l;i--){
int u=leaf[i].fi,son=leaf[i].se;
remove(son),clear_leaf(u);
}
}
}
// bool check_Ann_out(){
// if((int)ans.size()!=(n-1)){
// cerr<<ans.size()<<endl;
// return cerr<<"ans size is not true"<<endl,false;
// }
// for(int i=0;i<n-1;i++){
// int x=ans[i];
// if(G[x].size()!=1){
// cerr<<x<<':'<<G[x].size()<<'\n';
// cerr<<"the "<<i+1<<"th remove node ("<<x<<") is not leaf"<<endl;
// return false;
// }
// int y=G[x][0];
// G[y].erase(find(G[y].begin(),G[y].end(),x));
// G[x].clear();
// }
// return true;
// }
void Main(){
for(int i=1;i<n;i++){
int u,v; scanf("%d%d",&u,&v); u++,v++;
G[u].eb(v),G[v].eb(u);
}
p=q=0;
dfs0(1,0,p),dfs0(p,0,q);
if(dep[q]&1){
int rt=find_kfa(q,dep[q]/2);
dfs1(rt,0,1);
}
else{
int rt1=find_kfa(q,dep[q]/2-1),rt2=fa[rt1];
dfs1(rt1,rt2,1),dfs1(rt2,rt1,1),fa[rt1]=fa[rt2]=0;
}
solve_leaf();
for(int d=mxdep-1;d>=1;d--){
int u=-1;
for(int x:vec[d]) if(x!=fa[lst_del]&&appear[x]&&!del[x]){ u=x; break; }
remove(u),clear_leaf(fa[u]);
for(int x:vec[d]){
if(del[x]||!appear[x]) continue; //注意在删一个点的儿子时,必须在最开始先删掉一个出现过的儿子
remove(x),clear_leaf(fa[x]);
}
}
putchar(begin_op),puts(""); fflush(stdout);
for(int x:ans) printf("%d\n",x-1); fflush(stdout);
// if(check_Ann_out()) cerr<<"AC!!!Your ans is feasible"<<endl;
}
}
namespace Kathrin{
PII lst_leaf,lst_edge;
int lst_op;
bool appear[N];
char s[N];
void Main(){
scanf("%s",s+1);
for(int _=1;_<n;_++){
int u,v,leaf; scanf("%d%d",&u,&v);
if(!appear[u]&&!appear[v]){
int op;
if(_==1) op=s[1]-'0';
else if(mk(min(u,v),max(u,v))<lst_leaf) op=lst_op;
else op=lst_op^1;
if(op==1) leaf=min(u,v);
else leaf=max(u,v);
lst_op=op,lst_leaf=mk(min(u,v),max(u,v));
}
else if(u==lst_edge.fi||u==lst_edge.se) leaf=v;
else if(v==lst_edge.fi||v==lst_edge.se) leaf=u;
else if(appear[u]) leaf=u;
else leaf=v;
lst_edge={u,v},appear[u]=appear[v]=true;
printf("%d\n",leaf); fflush(stdout);
}
}
}
signed main(){
// freopen("Ann.in","r",stdin);
// freopen("Ann.out","w",stdout);
// freopen("Bob.in","r",stdin);
// freopen("Bob.out","w",stdout);
double beg=clock();
scanf("%d%d",&OP,&n);
if(OP==1) Ann::Main();
else Kathrin::Main();
cerr << "Time: " << (clock()-beg) << endl;
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号