闵可夫斯基和

定义

两个点集 \(A,B\) 的闵可夫斯基和 \(A+B\) 定义为：

\[A+B=\left \{ a+b | a\in A,b\in B \right \} \]

即把 \(B\) 中的每个点当做向量，然后让 \(A\) 中的点沿着这些向量平移，最终得到的点集就是他们的闵可夫斯基和。
这里我们只讨论凸包的闵可夫斯基和。

举个例子，下面这两个凸包（图是搬的）：

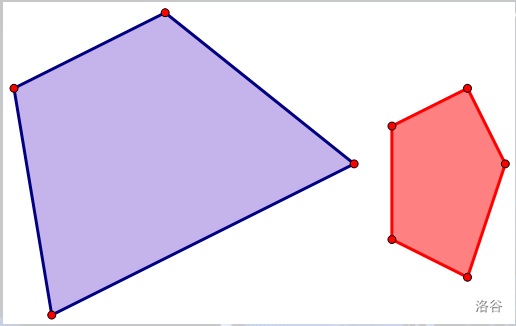
的闵可夫斯基和是（绿色边围起来的）：

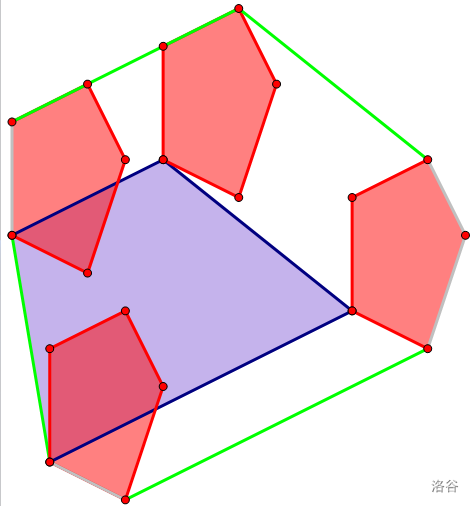
性质

根据观察~~因为我一个都不会证~~，两个凸包的闵可夫斯基和具有以下性质：

两个凸包的闵可夫斯基和还是一个凸包。
两个凸包的闵可夫斯基和所包含的边集恰好是这两个凸包的边集的并集，并且把这些边极角排序之后直接顺次连接起来即可。

实现

因为凸包的边集本身就是排好序的，所以把两个凸包的边集极角排序时可以直接归并，然后以 \(A_1+B_1\) 作为闵可夫斯基和的第一个点，顺次把边接上去即可。

void Minkowski_sum(Point *A,Point *B,Point *c,int &n,int &m,int &num){ //求两个凸包 A,B 的闵可夫斯基和，存在 c 中（A,B 中存的是点）
	num=0;
	c[++num]=A[1]+B[1];
	for(int i=1;i<=n;i++) t1[i]=A[i%n+1]-A[i];   
	for(int i=1;i<=m;i++) t2[i]=B[i%m+1]-B[i];
	int i=1,j=1;
	while(i<=n||j<=m){
		++num; 
		c[num]=c[num-1]+((j>m||(i<=n&&t1[i]*t2[j]>=0))?t1[i++]:t2[j++]);  //* 是叉积
	}
	num--;  //第一个点会被存两次
}

Tip：如果要求多个凸包的闵可夫斯基和，也可以直接把所有边放一起排序，比启发式合并等其他做法更简洁。

例题

I. [JSOI2018] 战争

题意：给定两个点集，设他们的凸包分别是 \(A,B\)，\(q\) 次询问，每次给定一个向量 \((dx,dy)\)，问把 \(B\) 平移向量 \((dx,dy)\) 后和 \(A\) 是否有交。

不妨设 \(k=(dx,dy)\)，有交意味着 \(\exists a\in A,b\in B\) 使得 \(a=b+k\)，即 \(k=a-b\)。
于是求出 \(A,-B\) 的闵可夫斯基和 \(C\)，然后就只需要判断 \(k\) 是否在 \(C\) 中。

关于判断平面上一个点是否在凸包内：
首先以这个凸包最左下的点为极点建立极坐标系，然后把 \(k\) 的终点放在这个极坐标系中，找到极角排序后他的前驱后继，比如在下图中极点是 \(O\)，\(k\) 的终点是 \(A\)，前驱后继分别是 \(B,C\)（注意这里需要判掉 \(A\) 在凸包外侧的情况）：

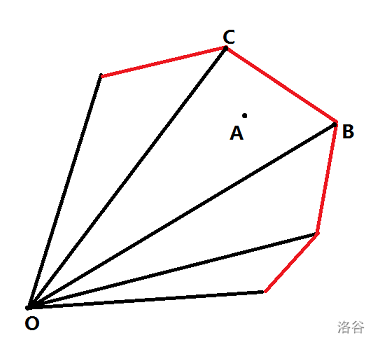
那么判断一下点 \(A\) 和线段 \(BC\) 的关系即可。

点击查看代码

#include<bits/stdc++.h>
#define Debug puts("-------------------------")
#define Point Vector
#define LL long long 
using namespace std;
const int N=1e5+5;

inline int read(){
	int w=1,s=0;
	char c=getchar();
	for(;c<'0'||c>'9';w*=(c=='-')?-1:1,c=getchar());
	for(;c>='0'&&c<='9';s=s*10+c-'0',c=getchar());
	return w*s;
}
int n,m,num,T;
struct Vector{
	LL x,y;
};
LL dist(Vector u){return u.x*u.x+u.y*u.y;} 
Vector operator + (const Vector &u,const Vector &v){return {u.x+v.x,u.y+v.y};}
Vector operator - (const Vector &u,const Vector &v){return {u.x-v.x,u.y-v.y};}
LL operator * (const Vector &u,const Vector &v){return u.x*v.y-u.y*v.x;}
bool cmp(Point u,Point v){return (u.x==v.x)?u.y<v.y:u.x<v.x;}
bool cmp2(Vector u,Vector v){return u*v>0||(u*v==0&&dist(u)<dist(v));}  
bool cmp3(Vector u,Vector v){return u*v>0||(u*v==0&&dist(u)>dist(v));}  

Point a[N],b[N],c[N],A[N],B[N],C[N],t1[N],t2[N];
int st[N],top; 
bool flag[N];
void Convec_Hull(Point *a,Point *A,int &n){   
	top=0;
	memset(flag,0,sizeof flag);
	sort(a+1,a+n+1,cmp);  
	st[++top]=1;  
	for(int i=2;i<=n;i++){  
		while(top>=2&&(a[st[top]]-a[st[top-1]])*(a[i]-a[st[top]])<=0) flag[st[top--]]=false;
		flag[i]=true,st[++top]=i;
	} 
	int siz=top;  
	for(int i=n;i>=1;i--){  
		if(flag[i]) continue;
		while(top>siz&&(a[st[top]]-a[st[top-1]])*(a[i]-a[st[top]])<=0) flag[st[top--]]=false;
		flag[i]=true,st[++top]=i;
	} 
	for(int i=1;i<top;i++) A[i]=a[st[i]]; 
	n=top-1; 
}
void Minkowski_sum(Point *A,Point *B,Point *c,int &n,int &m,int &num){
	num=0;
	c[++num]=A[1]+B[1];
	for(int i=1;i<=n;i++) t1[i]=A[i%n+1]-A[i];
	for(int i=1;i<=m;i++) t2[i]=B[i%m+1]-B[i];
	int i=1,j=1;
	while(i<=n||j<=m){
		++num;  
		c[num]=c[num-1]+((j>m||(i<=n&&t1[i]*t2[j]>=0))?t1[i++]:t2[j++]);
	}
	num--;
}
bool in(Vector k){
	if(cmp3(k,C[2])||cmp2(C[num],k)) return false;  //此时 k 在凸包外侧
	int l=lower_bound(C+1,C+num+1,k,cmp2)-C-1,r=l+1;
	return (k-C[l])*(C[r]-C[l])<=0;
}
signed main(){
	n=read(),m=read(),T=read();
	for(int i=1;i<=n;i++) a[i].x=read(),a[i].y=read();
	for(int i=1;i<=m;i++) b[i].x=-read(),b[i].y=-read();
	
	Convec_Hull(a,A,n);
	Convec_Hull(b,B,m);
	Minkowski_sum(A,B,c,n,m,num);
	Convec_Hull(c,C,num);
	Point s=C[1]; 
	for(int i=1;i<=num;i++) C[i]=C[i]-s; 
	while(T--){
		Point k={read(),read()}; k=k-s;   
		puts(in(k)?"1":"0");
	}
	return 0;
}

II. 叉积

题意：给定平面直角坐标系上的 \(n\)（\(n\le 10^5\)）个点 \(A_1,A_2,A_3,...\)，\(Q\) （\(Q\le 10^6\)）次询问，每次给定一个点 \(P\)，求使得 \(\sum_{i=l}^r \overrightarrow{OP} \times \overrightarrow{OA_i}\) 的值最大的区间 \([l,r]\)，并输出这个最大值（不用输出区间）。

设 \(\overrightarrow{OB_i}\) 是向量 \(\overrightarrow{OA_i}\) 的前缀和，向量集合 \(S=\left \{\overrightarrow{OB_j}-\overrightarrow{OB_i} | 0\le i<j\le n \right \}\)。
那么就是要从 \(S\) 中选出一个向量使得他和向量 \(\overrightarrow{OP}\) 的叉积尽可能大。
根据叉积的几何意义，这个向量的终点应该是 \(\overrightarrow{OP}\) 左侧，距离 \(OP\) 所在直线最远的（左侧没有的话就是右侧距离最近的）。
注意：\(\overrightarrow{OP}\) 左侧不一定是这条直线的上侧，如果 \(P\) 的横坐标是负的话那就是下侧了。
不难发现只有 \(S\) 内的点构成的凸包可能作为答案，所以我们只需要想办法求出这个凸包即可。

证：稍微说明一下这个结论的正确性，当 \(S\) 中存在 \(\overrightarrow{OP}\) 左侧的向量时，由于要求距离 \(\overrightarrow{OP}\) 最远的，所以求凸包显然没什么问题；而当不存在时，即 \(S\) 中的向量全都在 \(\overrightarrow{OP}\) 右侧，此时那些距离 \(\overrightarrow{OP}\) 比较近的点同样会保留在凸包上，并不会在求凸包的时候被弹掉，因此答案仍然在凸包上（而当存在至少一个 \(\overrightarrow{OP}\) 左侧的向量时，\(\overrightarrow{OP}\) 右侧距离它最近的点大概率不会出现在凸包中）。

考虑对 \(\overrightarrow{OB_i}\) 序列分治，假设现在的分治区间是 \([l,r]\)，那么 \([mid+1,r]\) 减去 \([l,mid]\) 构成的凸包可以用闵可夫斯基和求。
最后把所有闵可夫斯基和扔到一起求个凸包就好了。
求这个凸包的复杂度是 \(O(n\log^2 n)\)。

然后你一测大样例发现求出来的凸包大小都不超过 \(100\)，于是自信 \(O(q\times \text {凸包大小})\) 交一发就过了。

当然正经做法肯定是有的，应该可以根据凸包和直线的关系把凸包分成两个部分，然后分别在两部分上二分，不过可能细节有点多。

点击查看代码

#include<bits/stdc++.h>
#define Debug puts("-------------------------")
#define Point Vector
#define LL long long
using namespace std;
const int N=1e5+5,M=1e6+5,inf=LLONG_MIN;

inline int read(){
	int w=1,s=0;
	char c=getchar();
	for(;c<'0'||c>'9';w*=(c=='-')?-1:1,c=getchar());
	for(;c>='0'&&c<='9';s=s*10+c-'0',c=getchar());
	return w*s;
}
int n,m;
struct Vector{
	LL x,y;
}A[N],Q[M];
vector<Point> S,tmp;
Vector operator + (const Vector &u,const Vector &v){return {u.x+v.x,u.y+v.y};}
Vector operator - (const Vector &u,const Vector &v){return {u.x-v.x,u.y-v.y};}
LL operator * (const Vector &u,const Vector &v){return u.x*v.y-u.y*v.x;}
bool cmp(Point u,Point v){return (u.x==v.x)?u.y<v.y:u.x<v.x;}
int st[N*30],top;
bool flag[N*30]; 
void Convec_Hull(vector<Point> &a){
	int n=a.size();
	sort(a.begin(),a.end(),cmp);
	for(int i=0;i<n;i++) flag[i]=false;
	top=0;
	st[++top]=0;
	for(int i=1;i<n;i++){
		while(top>=2&&(a[st[top]]-a[st[top-1]])*(a[i]-a[st[top]])<=0) flag[st[top--]]=false;
		flag[st[++top]=i]=true;
	}
	int siz=top;
	for(int i=n-1;i>=0;i--){
		while(top>siz&&(a[st[top]]-a[st[top-1]])*(a[i]-a[st[top]])<=0) flag[st[top--]]=false;
		flag[st[++top]=i]=true;
	}
	tmp.resize(top-1);
	for(int i=1;i<top;i++) tmp[i-1]=a[st[i]];
	swap(a,tmp);
}
void Minkowski_sum(vector<Point> &a,vector<Point> &b,vector<Point> &res){
	int n=a.size(),m=b.size();
	res.resize(n+m+1);
	res[0]=a[0]+b[0];
	Vector tmp1=a[0]-a[n-1],tmp2=b[0]-b[m-1];
	for(int i=0;i<n-1;i++) a[i]=a[i+1]-a[i]; a[n-1]=tmp1;
	for(int i=0;i<m-1;i++) b[i]=b[i+1]-b[i]; b[m-1]=tmp2;
	int i=0,j=0,num=0;
	while(i<n||j<m){
		++num;
		res[num]=res[num-1]+((j>=m||(i<n&&a[i]*b[j]>=0))?a[i++]:b[j++]);
	}
	res.pop_back();
}
void solve(int l,int r){
	if(l==r) return;
	int mid=(l+r)>>1;
	solve(l,mid),solve(mid+1,r);
	vector<Point> v1,v2;
	for(int i=l;i<=mid;i++) v1.push_back({-A[i].x,-A[i].y});
	for(int i=mid+1;i<=r;i++) v2.push_back(A[i]);
	Convec_Hull(v1),Convec_Hull(v2);
	Minkowski_sum(v1,v2,tmp);
	for(Point u:tmp) S.push_back(u);
}
signed main(){
	freopen("cross.in","r",stdin);
	freopen("cross.out","w",stdout);
	n=read(),m=read();
	for(int i=1;i<=n;i++){
		A[i].x=read(),A[i].y=read(),A[i]=A[i-1]+A[i];
	}
	
	solve(0,n); Convec_Hull(S);
	
    略去求答案的部分
	
	return 0;
}

III.[KTSC 2022 R1] 直方图

题意够简洁了。

先对序列建出笛卡尔树，下面用 \(h_u\) 表示 \(u\) 代表的极大矩形的高度，\(len_u\) 代表长度，\(ls_u,rs_u\) 表示 \(u\) 的左右儿子，有时会用 \(u\) 直接表示 \(u\) 代表的极大矩形。

\(f(1)=\max(len_u \times h_u)\)。

\(f(2)\)

假设最终的结果是 \(u,v\) 两个矩形的并集。
有两种情况，一种是两个矩形无交，即 \(u,v\) 在树上没有祖先关系，这个答案是好求的。
还有一种是在树上有祖先关系，不妨设 \(u\) 是 \(v\) 的祖先，那么面积是 \(len_u\times h_u+len_v\times h_v-len_v\times h_u\)，我们在 \(u\) 处统计答案，用李超树维护子树内形如 \((-len_v,len_v \times h_v)\) 的这些直线，查询 \(x=h_u\) 处的最大值。合并两棵子树时用李超树合并。

关于李超树合并的复杂度：因为李超树是标记永久化的，所以在动态开点时插入一个直线只会最多新建一个节点，因此总结点数是 \(O(n)\) 的，一个节点上的线段如果下传了那么会使深度 \(+1\)，而深度最大是 \(O(\log n)\)，所以总复杂度是 \(O(n\log n)\)。

\(f(3)\)

假设最终的结果是 \(u,v,w\) 三个矩形合并的结果。

\(u,v,w\) 互不相交：简单树形 DP 即可。
\(u\) 是 \(v\) 的祖先，但 \(w\) 和他们都不交：类似 \(f(2)\) 中不交的情况做即可。
\(u\) 是 \(v\) 的祖先，\(v\) 是 \(w\) 的祖先（其他顺序同理）：在 \(f(2)\) 有祖先关系的情况的基础上，设 \(g_u\) 表示 \(u\) 和他的子树中的一个点 \(v\) 并起来的最大面积，那么这种情况的答案是 \(len_u\times h_u+g_v-len_v\times h_u\)，同样用李超树维护 \((-len_v,g_v)\) 这些直线。

最后一种情况是 \(u\) 是 \(v,w\) 的祖先，但 \(v,w\) 这两个点不交。
此时面积并是 \(len_u\times h_u+len_v\times h_v+len_w\times h_w-(len_v+len_w)\times h_u\)，可以发现如果 \(u\) 不是 \(v\) 或 \(w\) 的祖先，这个东西只会算的更小，所以可以去掉 \(u\) 是 \(v,w\) 的祖先这个限制。
如果此时没有 \(v,w\) 不交这个限制，那么相当于是先求出所有形如 \((len_v,len_v\times h_v)\) 的点的凸包（注意此时我们把他看成点而非直线，所以是 \(len_v\) 而不是 \(-len_v\)），然后和自己做闵可夫斯基和，在得到的新凸包上用斜率为 \(h_u\) 的直线去切他。
考虑怎么处理 \(v,w\) 不交这个限制，我们用他们的子树在 \(dfn\) 上的区间来刻画他们是否相交，然后类比上一题的思路，考虑分治。如果当前分治区间是 \([l,r]\) 就把所有右端点在 \([l,mid]\) 中的点的凸包和所有左端点在 \([mid+1,r]\) 中的点的凸包做闵可夫斯基和，最后把所有闵可夫斯基和合并一下即可。

总复杂度 \(O(n\log^2 n)\)。

点击查看代码

#include<bits/stdc++.h>
#define LL long long 
#define Point Vector
#define eb emplace_back
std::vector<long long> max_area(std::vector<int> H);
using namespace std;
const int N=5e5+5,V=5e5;

int n,h[N],ls[N],rs[N],st[N*20],top,rt,len[N],dfn[N],num;
LL maxn[N],S[N];
LL ans1,ans2,ans3;
void dfs0(int u){
	if(!u) return;
	dfn[u]=++num;
	dfs0(ls[u]),dfs0(rs[u]);
	len[u]=1+len[ls[u]]+len[rs[u]];
	S[u]=1ll*len[u]*h[u];
	maxn[u]=max({maxn[ls[u]],maxn[rs[u]],S[u]});
}
void Init(){
	for(int i=1;i<=n;i++){
		int v=0;
		while(top&&h[st[top]]>h[i]) v=st[top],top--;
		if(top) rs[st[top]]=i;
		ls[i]=v,st[++top]=i;
	}
	rt=st[1];
	dfs0(rt);
}

void solve1(){ ans1=maxn[rt]; }

struct LiChaoSegmentTree{
	int tot;
	struct node{
		int ls,rs,k; LL b;
	}t[N*20];
	LL calc(int k,LL b,int x){ return 1ll*k*x+b; }
	int New(int k,LL b){
		t[++tot]={0,0,k,b};
		return tot;
	}
	void update(int &p,int l,int r,int k,LL b){
		if(!p) return p=New(k,b),void();
		int mid=(l+r)>>1;
		if(calc(k,b,mid)>calc(t[p].k,t[p].b,mid)) swap(k,t[p].k),swap(b,t[p].b);
		if(l==r) return;
		if(calc(k,b,l)>calc(t[p].k,t[p].b,l)) update(t[p].ls,l,mid,k,b);
		else if(calc(k,b,r)>calc(t[p].k,t[p].b,r)) update(t[p].rs,mid+1,r,k,b);
	}
	int merge(int p,int q,int l,int r){
		if(!p||!q) return p|q;
		update(p,l,r,t[q].k,t[q].b);
		if(l==r) return p;
		int mid=(l+r)>>1;
		t[p].ls=merge(t[p].ls,t[q].ls,l,mid);
		t[p].rs=merge(t[p].rs,t[q].rs,mid+1,r);
		return p;
	}
	LL ask(int p,int l,int r,int x){
		if(!p) return 0;
		LL res=calc(t[p].k,t[p].b,x);
		if(l==r) return res;
		int mid=(l+r)>>1;
		if(x<=mid) return max(res,ask(t[p].ls,l,mid,x));
		else return max(res,ask(t[p].rs,mid+1,r,x));
	}
}Seg;
int root[N];
LL G[N],g[N];
void dfs1(int u){
	if(!u) return;
	ans2=max(ans2,maxn[ls[u]]+maxn[rs[u]]);
	dfs1(ls[u]),dfs1(rs[u]);
	root[u]=Seg.merge(root[ls[u]],root[rs[u]],1,V);
	G[u]=Seg.ask(root[u],1,V,h[u])+S[u];
	g[u]=max({g[ls[u]],g[rs[u]],G[u]});
	Seg.update(root[u],1,V,-len[u],S[u]);
}
void solve2(){ dfs1(rt); ans2=max(ans2,g[rt]); }

LL f[N][3];
vector<int> L[N],R[N];
struct Vector{
	LL x,y;
};
vector<Point> All,tmp;
Vector operator + (const Vector &u,const Vector &v){return {u.x+v.x,u.y+v.y};}
Vector operator - (const Vector &u,const Vector &v){return {u.x-v.x,u.y-v.y};}
LL operator * (const Vector &u,const Vector &v){return u.x*v.y-u.y*v.x;}
bool cmp(Point u,Point v){return (u.x==v.x)?u.y<v.y:u.x<v.x;}
void Convec_Hull(vector<Point> &a){
	int n=a.size();
	sort(a.begin(),a.end(),cmp);
	st[top=1]=0;
	for(int i=1;i<n;i++){
		while(top>=2&&(a[i]-a[st[top]])*(a[st[top]]-a[st[top-1]])<=0) top--;
		st[++top]=i;
	}
	tmp.resize(top);
	for(int i=1;i<=top;i++) tmp[i-1]=a[st[i]];
	swap(a,tmp);
}
void Minkowski_sum(vector<Point> &a,vector<Point> &b,vector<Point> &res){
	int n=a.size()-1,m=b.size()-1;  //n,m 是边数 
	res.resize(n+m+1);
	res[0]=a[0]+b[0];
	for(int i=0;i<n;i++) a[i]=a[i+1]-a[i]; 
	for(int i=0;i<m;i++) b[i]=b[i+1]-b[i]; 
	int i=0,j=0,num=0;
	while(i<n||j<m){
		++num;
		res[num]=res[num-1]+((j>=m||(i<n&&a[i]*b[j]<=0))?a[i++]:b[j++]);
	}
}
void dfs2(int u){
	if(!u) return;
	ans3=max({ans3,maxn[ls[u]]+g[rs[u]],g[ls[u]]+maxn[rs[u]]});  //两个有交，但和另外一个都不交 
	dfs2(ls[u]),dfs2(rs[u]);
	f[u][0]=maxn[u];
	f[u][1]=max({f[ls[u]][1],f[rs[u]][1],maxn[ls[u]]+maxn[rs[u]]});
	f[u][2]=max({f[ls[u]][2],f[rs[u]][2],f[ls[u]][0]+f[rs[u]][1],f[ls[u]][1]+f[rs[u]][0]});  
	
	root[u]=Seg.merge(root[ls[u]],root[rs[u]],1,V);
	ans3=max(ans3,Seg.ask(root[u],1,V,h[u])+S[u]);  //三个矩形全部有交 
	Seg.update(root[u],1,V,-len[u],G[u]);
}
void work(int l,int r){
	if(l==r) return;
	int mid=(l+r)>>1;
	work(l,mid),work(mid+1,r);
	vector<Point> a,b;
	for(int i=l;i<=mid;i++) for(int u:R[i]) a.push_back({len[u],S[u]}); 
	for(int i=mid+1;i<=r;i++) for(int u:L[i]) b.push_back({len[u],S[u]}); 
	if(a.empty()||b.empty()) return;
	Convec_Hull(a),Convec_Hull(b),Minkowski_sum(a,b,tmp);
	for(Point u:tmp) All.push_back(u);
}
LL ask(LL k){
	int l=0,r=All.size()-2,mid,res=All.size()-1;
	while(l<=r){
		mid=(l+r)>>1;
		if(k*(All[mid+1].x-All[mid].x)>(All[mid+1].y-All[mid].y)) res=mid,r=mid-1;
		else l=mid+1;
	}
	return All[res].y-All[res].x*k;
}
void solve3(){
	for(int i=1;i<=n;i++) root[i]=0,L[dfn[i]].eb(i),R[dfn[i]+len[i]-1].eb(i);
	Seg.tot=0;
	dfs2(rt);
	ans3=max(ans3,f[rt][2]); //三个矩形全部不交 
	work(1,n);
	if(All.empty()) return;
	Convec_Hull(All);
	for(int i=1;i<=n;i++) ans3=max(ans3,ask(h[i])+S[i]);  //一个矩形是两个矩形的父亲，但是另两个矩形不交
}
vector<LL> max_area(vector<int> H){
	n=H.size();
	for(int i=1;i<=n;i++) h[i]=H[i-1];
	Init();
	solve1(),solve2(),solve3();
	vector<LL> ans(3);
	ans[0]=ans1,ans[1]=ans2,ans[2]=ans3;
	return ans;
}

posted @ 2025-07-02 18:39 Green&White 阅读(192) 评论(0) 收藏举报

刷新页面返回顶部

OIer_Cyq

闵可夫斯基和

闵可夫斯基和

定义

性质

实现

例题

I. [JSOI2018] 战争

II. 叉积

III.[KTSC 2022 R1] 直方图

\(f(2)\)

\(f(3)\)

公告