Vector 加减乘除

//  l 的头，与 r 的尾巴连接起来， l的尾巴与r的头组成一个新的vector
vec2 operator+(const vec2& l, const vec2& r) {
    return { l.x + r.x, l.y + r.y };
}

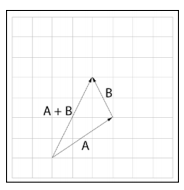
//  l 与 r 的尾部相连，从 r 的头部出发连接到 l 的头部，构建新的Vector
vec2 operator-(const vec2& l, const vec2& r) {
    return { l.x - r.x,l.y - r.y };
}

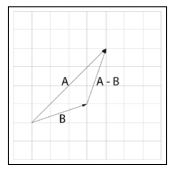也可以理解成 A+（-B）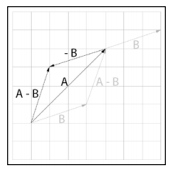

// 就是把 l 拉长，两种情况的区别是，乘 float 时，整体拉长，乘 vec2时 x，y轴相应拉长
vec2 operator*(const vec2& l, const vec2& r) {
    return { l.x * r.x, l.y * r.y };
}

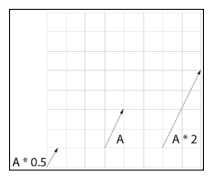
//  >0 方向相同， < 0 方向相反， == 0 垂直 几何意义: A·B = |A||B|cosθ
float dot(const vec2& l, const vec2& r){
    return l.x * r.x + l.y + r.y;
}

 

// 计算长度, 由于开平方比较慢,所以如果只是需要做比较的话
// a * a > length * length 即可
float Magnitude(const vec2& v){
    return Dot(v,v);
}

 

// 归一化之后, 就可以直接与速度相乘,来表示朝某方向前进了
void Normalize(vec2& v){
    v = v * (1.0f / Magnitude(v));
}

 

/// <summary>
/// 投影
/// A` = dot(A,B)/Magitude(B)*Magitude(B)*B/// </summary>
/// <param name="len"></param>
/// <param name="dir"></param>
/// <returns></returns>
vec2 Project(const vec2& len, const vec2 dir) {
    float dot = Dot(len, dir);
    float magSq = MagnitudeSq(dir);
    return dir * (dot / magSq);
}

 

/// <summary>
/// R = V - 2(Project(V,N)N;
/// 当normal为单位向量时  Project(V,N) = 1 * Dot(V,N) / 1; 
/// R = V - 2(Dot(V,N)N;
/// </summary>
/// <param name="vec"></param>
/// <param name="normal"></param>
/// <returns></returns>
vec2 Reflection(const vec2& vec, const vec2 normal){
    float d = Dot(vec, normal);
    return vec - normal * (d * 2.0f);
}