【图像处理笔记】特征提取之区域特征
0 引言
图像分割为多个区域或它们的边界后,需要进行特征提取,特征提取包括特征检测和特征描述。特征检测是指在边界、区域或图像中发现特征,特征描述是将定量属性分配给检测到的特征。例如,可以检测一个区域边界上的角,并用它们的方向和位置来描述这些角,其中的方向和位置都是定量属性。在特征提取之前,应尽可能利用预处理来归一化输入图像。例如,在照度变化严重到难以提取特征时,通过直方图均衡化来自动地预处理图像。基本思想是,使用极可能多的先验信息来预处理图像,以提高特征提取得准确性。
特征分为不变的和协变的。比如,考虑一组变换{平移,反射,旋转},“面积”是一个不变的特征描述子。在加入{缩放}后,“面积”相对于这组变换是协变的,因为对区域面积缩放任意一个引子,也会对描述子的值缩放相同的因子。描述子“方向”(这个区域的主轴方向)也是协变的。本章大多数描述子都是协变的,最好的做法是将协变性归一化为相关的不变性。例如,通过计算一个区域的实际方向并旋转该区域,使其主轴指向预定义的方向,可以补偿这个区域方向的变化。如果对图像中检测到的每个区域都这样做,那么旋转就不再是协变的。特征的另一个主要分类是特征分为局部特征和全局特征,如果某个特征被用应用到一个集合的一个成员,那么我们称它为局部特征;如果某个特征被应用到整个集合,那么我们称它为全局特征。
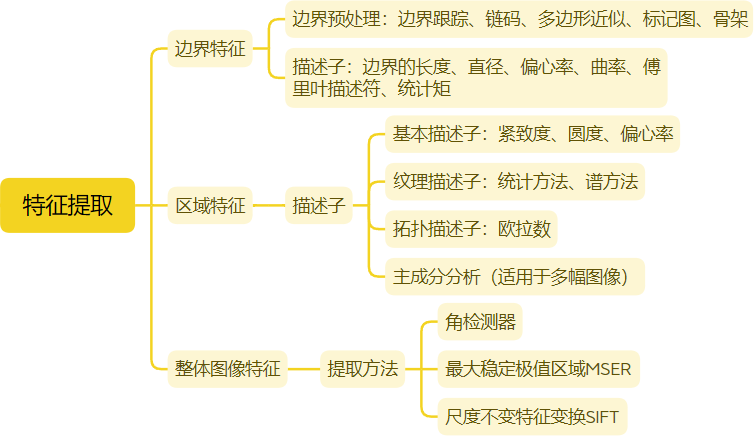
1 区域特征描述子
1.1 一些基本描述子
针对目标所在区域的特征描述符(Region descriptors),称为区域特征描述子。例如:- 紧致度(compactness):周长的平方与面积之比,具有平移、尺度、旋转不变性;
- 圆度(circularity):4pi*面积与周长的平方之比,具有平移、尺度、旋转不变性;
- 偏心率(Eccentricity):椭圆的偏心率定义为焦距与椭圆长轴的长度之比。对给定二维区域计算偏心率时,要用一个椭圆区域近似二维数据,这个椭圆的轴要与数据的主轴重合。
示例 特征描述子的比较
Mat src = imread("./6.bmp", 0);
Mat markImg = Mat::zeros(src.size(), CV_8UC3);
vector<vector<Point>> contours; vector<Vec4i> hierarchy;
findContours(src, contours, hierarchy, RETR_EXTERNAL, CHAIN_APPROX_NONE);
for (int i = 0; i < contours.size(); i++) {
cout << "##### contours - " << to_string(i) << "#####" << endl;
double area = contourArea(contours[i]);
double len = arcLength(contours[i], true);
RotatedRect rr = fitEllipse(contours[i]);
double a = rr.size.width > rr.size.height ? rr.size.width : rr.size.height;
double c = sqrt(abs(pow(rr.size.width, 2) - pow(rr.size.height, 2)));
double compactness = len * len / area;
cout << "compactness:" << compactness << endl;
double circularity = 4 * CV_PI * area / len / len;
cout << "circularity:" << circularity << endl;
double eccentricity = c / a;
cout << "eccentricity:" << eccentricity << endl;
drawContours(markImg, contours, i, Scalar(0, 255, 0), 1);
}

1.2 拓扑描述子
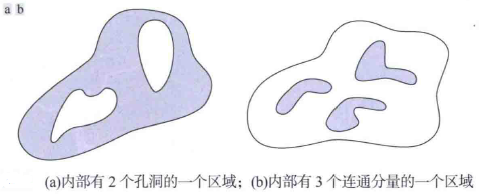
拓扑学研究的是图形不受任何变形影响的性质,前提是图形未被撕裂或拼合(有时将这些变形称为橡胶膜变形)。由于拉伸会影响距离,因此拓扑性质既不依赖于距离,又不依赖于基于距离测度的任何性质。例如下图(a)显示了一个内部有两个孔洞的区域。显然,将拓扑描述子定义为这个区域的孔洞数量不会受到拉伸或旋转的影响。对区域描述有用的另一个拓扑性质是图像或区域的连通分量的数量。下图(b)显示了一个内部有3个连通分量的区域。拓扑描述子欧拉数E定义为目标区域的连通分量的数量 C 与孔洞数量 H 的差:E = C − H。
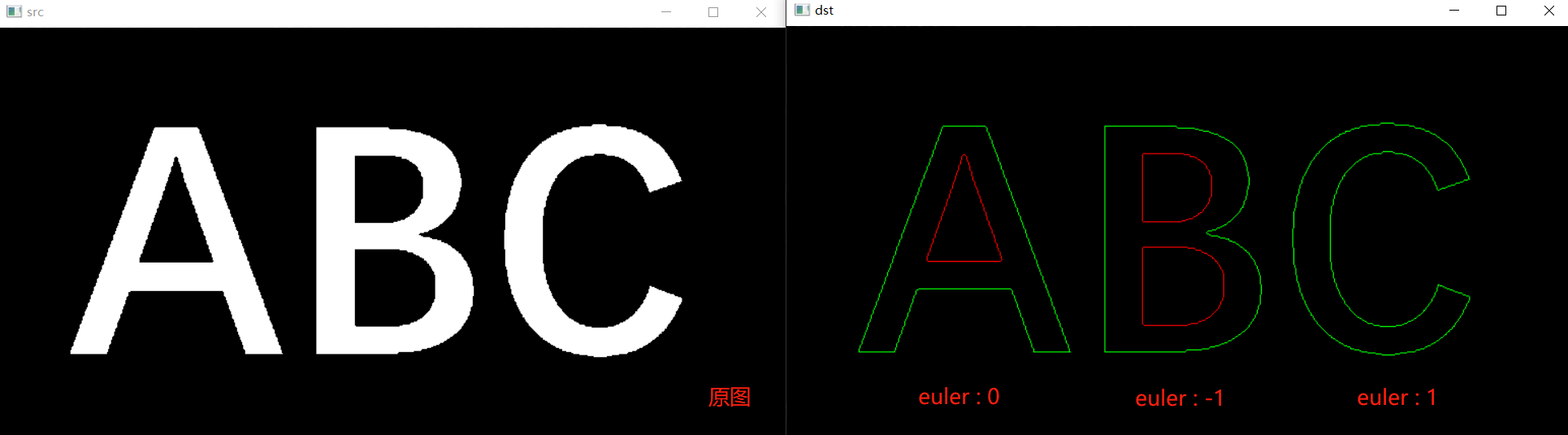
示例 利用轮廓的层次信息计算欧拉数
Mat src = imread("./4.bmp", 0);
Mat markImg = Mat::zeros(src.size(), CV_8UC3);
vector<vector<Point>> contours; vector<Vec4i> hierarchy;
findContours(src, contours, hierarchy, RETR_CCOMP, CHAIN_APPROX_NONE);
for (int i = 0; i < contours.size(); i++) {
if (hierarchy[i][3] == -1) {
int c = 1; int h = 0;
drawContours(markImg, contours, i, Scalar(0, 255, 0), 1);
int child_index = hierarchy[i][2];
while (child_index != -1) {
h++;
drawContours(markImg, contours, child_index, Scalar(0, 0, 255), 1);
int next_index = hierarchy[child_index][0];
child_index = next_index;
}
cout << "euler:" << c - h << endl;
}
}
1.3 纹理
纹理提供了诸如平滑度、粗糙度和规则性等性质的测度,可以用统计方法和谱方法描述。统计方法产生光滑、粗糙、颗粒等纹理特征。谱方法就与傅里叶频谱的性质,主要通过识别频谱中的高能量窄峰来检测图像中的全局周期性。
1.3.1 统计方法之统计矩
描述纹理的最简单的方法之一是,使用图像或区域的灰度直方图的统计矩。令z是一个表示灰度的随机变量,并令p(zi),i=0,1,2,...,L-1是对应的归一化直方图,其中L是不同灰度级的数量。z相对于平均值的n阶矩是
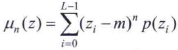
式中m是z的均值(即图像或区域的平局灰度)。由上式可得,μ0=1,μ1=0,。二阶矩μ2(即方差)灰度对比的一个测度,可用于建立相对灰度平滑度描述子:
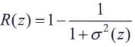
对于恒定灰度区域(其方差为零),R为0,相对于较大的σ2(z)值,测度接近1。由于灰度图像的值域通常是从0到255,其方差值往往较大。因此,需将σ2(z)除以(L-1)2进行归一化到区间[0,1]内再计算R。标准差σ2(z)也频繁用做纹理的一个测度,因为它的值更直观。三阶矩μ3是直方图的偏斜度的一个测度,四阶矩μ4是相对平坦度的一个测度。五阶矩和更高阶的矩很难与直方图的形状关联起来,但它们的确能够进一步定量地描述纹理内容。基于直方图的其他一些有用的纹理测度包括一致性测度:

由于p值得范围是[0,1],并且它们的和等于1,所以对所有灰度级相等的图像,描述子U的值是最大的,并且从那里开始减小。平均熵测度是可变性的一个测度,恒定图像的熵是0,定义为:
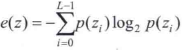
示例 基于直方图的纹理描述子
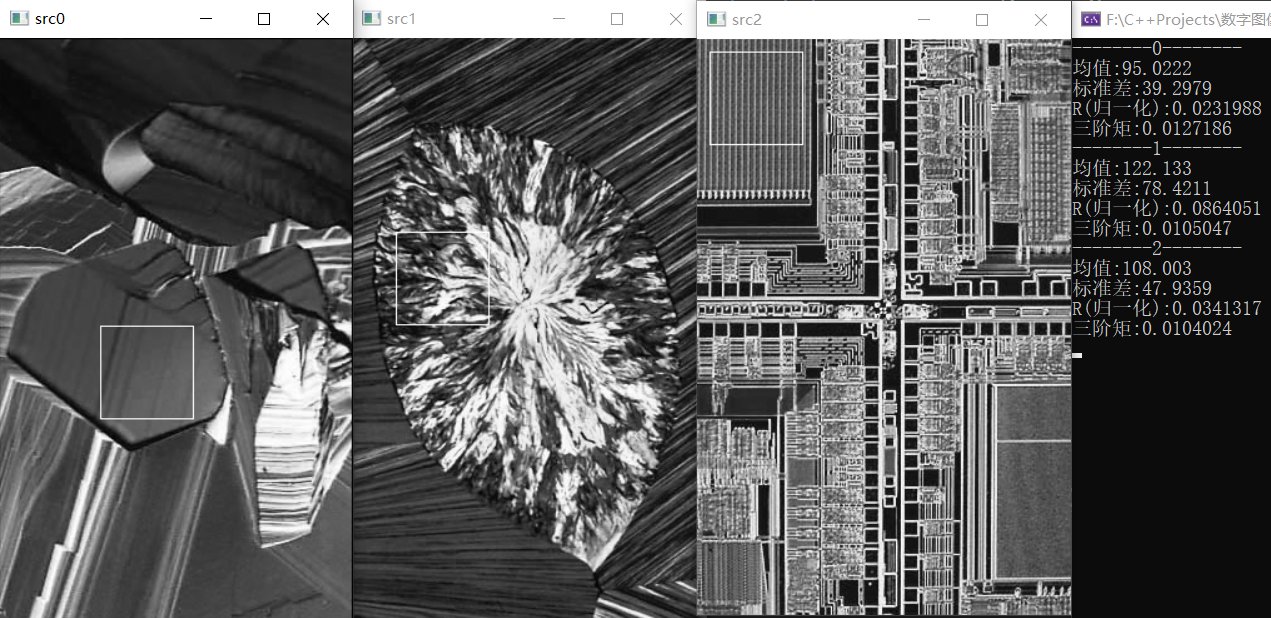
下面从左到右的白色正方形标记分别是平滑的纹理,粗糙的纹理和规则的纹理。这些图像分别是超导体、人体胆固醇和微处理器的光学显微镜图像。三阶矩可以判断直方图的对称性,是偏向均值的左侧(暗侧)还是偏向均值的右侧(亮侧),但是,就纹理而言,只有当测度之间的变化较大时,由三阶矩得到的信息才是有用的。
#include <opencv2/opencv.hpp>
using namespace cv;
using namespace std;
int main() {
string filepath = "./纹理";
vector<string> filenames;
glob(filepath, filenames);
vector<Rect> rects = { Rect(80, 230, 75, 75), Rect(35, 155, 75, 75), Rect(10, 10, 75, 75) };
for (int n = 0; n < filenames.size(); n++) {
Mat src = imread(filenames[n], 0);
Rect r = rects[n];
rectangle(src, r, Scalar(255), 1);
Mat roi = src(r);
// 灰度直方图
int histsize = 256;
float range[] = { 0, 256 };
const float* ranges = { range };
Mat hist;
calcHist(&roi, 1, 0, Mat(), hist, 1, &histsize, &ranges);
int totalGray = sum(roi)[0];
int totalPixels = roi.rows * roi.cols;
double m = totalGray * 1.0 / totalPixels;
double R = 0; double moment2 = 0; double moment3 = 0;
for (int i = 0; i < 256; i++) {
moment2 += pow((i - m), 2) * hist.at<float>(i, 0) / totalPixels;
moment3 += pow((i - m), 3) * hist.at<float>(i, 0) / totalPixels;
}
cout << "均值:" << m << endl;
cout << "标准差:" << sqrt(moment2) << endl;
cout << "R(归一化):" << 1- 1/(1+moment2/ pow(255, 2)) << endl;
cout << "三阶矩:" << moment3/pow(255,3) << endl;
}
return 0;
}
1.3.2 统计方法之灰度共生矩阵
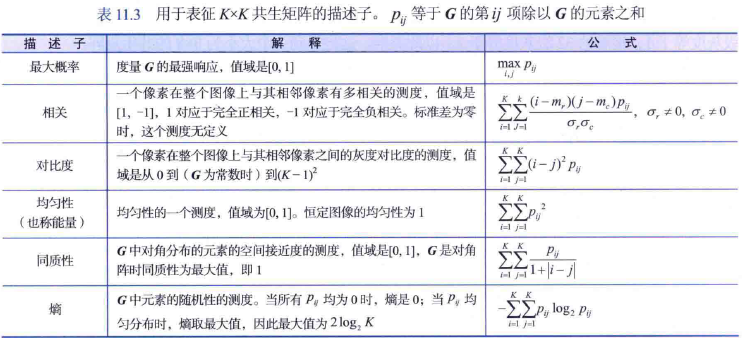
在描述纹理时,空间信息非常重要,即不仅要考虑灰度的分布,而且要考虑像素在图像中的相对位置。上节直方图计算的纹理测度不携带像素间的空间关系信息,本节介绍的灰度共生矩阵描述了空间上具有某种分布规律的灰度值组合出现的概率。灰度共生矩阵的定义是,从灰度为i的像素点出发,距离(a,b) 的另一像素点 (x+a,y+b) 的灰度为j的概率。所有的估计值表示为矩阵矩式,称为灰度共生矩阵。灰度共生矩阵在点 (x,y) 处的值,表示了特定灰度值组合在图像中出现的频次:
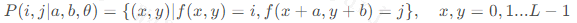
式中:
a,b 为距离差分值,也称相邻间隔、偏移量,要根据纹理周期分布的特性来选择,无特性参数时取 1(像素);
θ 为扫描方向,通常选择 0°,45°,90°,135°,对应以水平、垂直和左右对角线方向扫描像素对组合;
i,j=0,...L−1 表示像素的灰度级。灰度级 L=256 时即为灰度值,也可以取其它灰度级如 L=8,16。共生矩阵有方向和步长的组合,是一个稀疏矩阵,灰度级划分常常减少到8级。显然,灰度共生矩阵的尺寸为 L*L,而与图像尺寸无关。
也就是说,灰度共生矩阵中点 (i,j) 的值,就是灰度值为 i,j 的联合概率密度。因此,灰度共生矩阵能反映出图象灰度关于方向、相邻间隔、变化幅度的综合信息,是分析图象的局部模式和它们排列规则的基础。
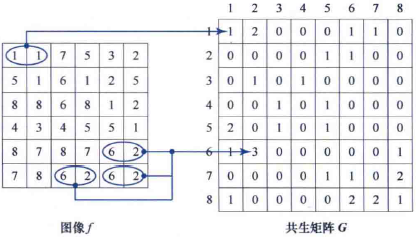
示例 当a=1, b=0, θ=0 时6×6矩阵(L=8)的灰度共生矩阵(未归一化)
Mat f = (Mat_<uchar>(6, 6) <<
1, 1, 7, 5, 3, 2,
5, 1, 6, 1, 2, 5,
8, 8, 6, 8, 1, 2,
4, 3, 4, 5, 5, 1,
8, 7, 8, 7, 6, 2,
7, 8, 6, 2, 6, 2
);
Mat g = Mat::zeros(Size(8, 8), CV_8UC1);
for (int i = 0; i < f.rows; i++) {
uchar* p = f.ptr<uchar>(i);
for (int j = 0; j < f.cols - 1; j++) {
int a = (int)p[j];
int b = (int)p[j + 1];
g.at<uchar>(a - 1, b - 1) += 1;
}
}
1.3.3 谱方法
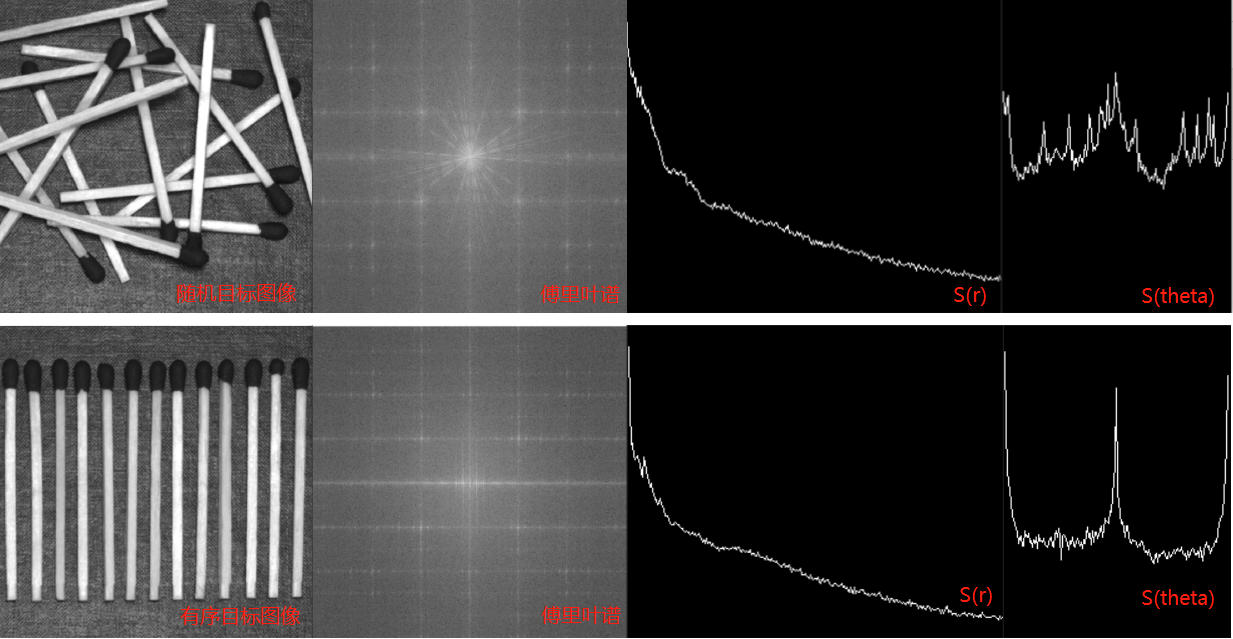
傅里叶谱可以描述图像中的周期性或半周期性二维模式的方向性,因此可以基于傅里叶变换对纹理进行频谱分析。纹理与图像频谱中的高频分量密切相关,纹理模式在频谱图表现为高能量的爆发。
傅里叶谱具有三个特征可以描述纹理的性质:
(1)傅里叶频谱中的突出峰值对应于纹理模式的主方向;
(2)频域图中的峰值位置对应于纹理模式在空间上的基本周期;
(3)通过滤波消除周期分量,用统计方法描述剩下的非周期性信号。
把傅里叶幅度谱转换到极坐标中表示为函数S(r,θ),可以简化对频谱特性的解释。S 是频谱函数,r 和θ 是极坐标系的半径和角度坐标轴。S 对于每一个方向θ可以简化为一维函数Sθ(r);S 对于每一个半径 r 也可以简化为一维函数Sr(θ)。分别对一维函数 Sθ(r)和 Sr(θ)积分,可以获得纹理频谱的全局描述:
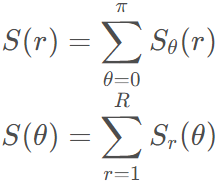
如果纹理具有空间的周期性或确定的方向性,则一维函数S(r)和S(θ)在对应的频率具有峰值。
示例 特征描述之傅里叶频谱纹理分析
Mat fftshift(Mat& magMat) {
Mat magImg(magMat.size(), CV_8UC1);
magMat.convertTo(magImg, CV_8UC1, 255, 0);
magMat = magMat(Rect(0, 0, magMat.cols & -2, magMat.rows & -2));
int cx = magImg.cols / 2;
int cy = magImg.rows / 2;
Mat q1 = magImg({ 0, 0, cx, cy });
Mat q2 = magImg({ 0, cy, cx, cy });
Mat q3 = magImg({ cx, 0, cx, cy });
Mat q4 = magImg({ cx, cy, cx, cy });
Mat temp;
q1.copyTo(temp);
q4.copyTo(q1);
temp.copyTo(q4);
q2.copyTo(temp);
q3.copyTo(q2);
temp.copyTo(q3);
return magImg;
}
int main() {
Mat src = imread("./8.tif", 0);
// 傅里叶变换
Mat planes[] = { Mat_<float>(src), Mat::zeros(src.size(),CV_32FC1) };
Mat comImg, dftImg;
merge(planes, 2, comImg);
dft(comImg, dftImg, DFT_COMPLEX_OUTPUT);
split(dftImg, planes);
Mat magMat;
magnitude(planes[0], planes[1], magMat);//计算幅度谱
magMat += Scalar::all(1);
log(magMat, magMat);
normalize(magMat, magMat, 0, 1, NORM_MINMAX);
Mat magImg = fftshift(magMat);//将低频分量移动到频域图像的中心
// 频谱沿半径的分布函数
int sr[300] = { 0 };
for (int radius = 1; radius < 300; radius++) {
for (int degree = 0; degree < 180; degree++) {
double theta = degree * CV_PI / 180;
int x = (int)(magImg.cols / 2 + radius * cos(theta));
int y = (int)(magImg.rows / 2 + radius * sin(theta));
sr[radius] += (int)magImg.at<uchar>(y, x);
}
}
// 频谱沿角度的分布函数
int st[180] = { 0 };
for (int degree = 0; degree < 180; degree++) {
for (int radius = 1; radius < 300; radius++) {
double theta = degree * CV_PI / 180;
int x = (int)(magImg.cols / 2 + radius * cos(theta));
int y = (int)(magImg.rows / 2 + radius * sin(theta));
st[degree] += (int)magImg.at<uchar>(y, x);
}
}
// 绘制
Mat mask = Mat::zeros(250, 300, CV_8UC1);
for (int i = 1; i < 299; i++) {
Point2f p0 = Point2f(i, 400-sr[i]/100.0 );
Point2f p1 = Point2f(i + 1, 400 - sr[i + 1] / 100.0);
line(mask, p0, p1, Scalar(255), 1);
}
Mat mask1 = Mat::zeros(250, 182, CV_8UC1);
for (int i = 1; i < 179; i++) {
Point2f p0 = Point2f(i, 850 - st[i] / 50.0);
Point2f p1 = Point2f(i + 1, 850 - st[i + 1] / 50.0);
line(mask1, p0, p1, Scalar(255), 1);
}
return 0;
}
1.4 矩不变量


示例 矩不变量
本例的目的是用下图中的图像计算和比较前述的矩不变量。本例中的图像添加了黑色(0)边框,目的是使用所有图像的大小相同;零不影响矩不变量的计算。下面分别显示了图像被平移、缩放0.5、镜像、旋转45°、旋转90°后的图像。我们感兴趣的是矩的不变性和相对符号,而不是它们的实际值,为了减小动态范围并简化解释,数值进行了缩放。输出结果的关键点是:(1)矩不变量独立于平移、缩放、镜像和旋转;(2)Φ7的符号对镜像图像是不同的。
int sgn(double x) {
if (x > 0)
return 1;
else if (x < 0)
return -1;
else
return 0;
}
int main() {
string filepath = "./矩不变量";
vector<string> filenames;
glob(filepath, filenames);
for (int n = 0; n < filenames.size(); n++) {
Mat src = imread(filenames[n], 0);
Moments m = moments(src);
double hu[7];
HuMoments(m, hu);
cout << "【picture" << to_string(n + 1) << "】";
for (int i = 0; i < 7; i++)
cout << "hu" << to_string(i + 1) << ": " << -sgn(hu[i]) * log10(abs(hu[i])) << " ";
cout << endl;
}
}


2 习题
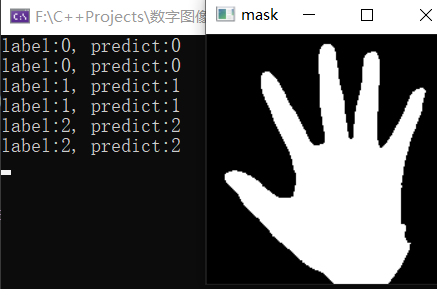
2.1 手势识别
参考博客《opencv手势识别》,利用32位傅里叶描述子描述手势轮廓,训练SVM模型并预测。
#include <opencv2/opencv.hpp>
#include <iostream>
#include <fstream>
using namespace cv::ml;
using namespace std;
using namespace cv;
int n_dims = 32;
int n_class = 3;
int n_samples = 30;
// 输入轮廓,得到傅里叶描述子
vector<double> FourierShapeDescriptors(vector<Point>& contour)
{
vector<double> fd(32);
//计算轮廓的傅里叶描述子
Point p;
int x, y, s;
int i = 0, j = 0, u = 0;
s = (int)contour.size();
float f[9000];//轮廓的实际描述子
for (u = 0; u < contour.size(); u++)
{
float sumx = 0, sumy = 0;
for (j = 0; j < s; j++)
{
p = contour.at(j);
x = p.x;
y = p.y;
sumx += (float)(x * cos(2 * CV_PI * u * j / s) + y * sin(2 * CV_PI * u * j / s));
sumy += (float)(y * cos(2 * CV_PI * u * j / s) - x * sin(2 * CV_PI * u * j / s));
}
f[u] = sqrt((sumx * sumx) + (sumy * sumy));
}
//傅立叶描述子的归一化
f[0] = 0;
fd[0] = 0;
for (int k = 2; k < n_dims + 1; k++)
{
f[k] = f[k] / f[1];
fd[k - 1] = f[k];
}
return fd;
}
// 输入轮廓,得到Hu矩
vector<double> huDescriptors(vector<Point>& contour) {
Moments m = moments(contour);
double hu[7]; vector<double> hus;
HuMoments(m, hu);
for (int i = 0; i < 7; i++) {
hus.push_back(hu[i]);
}
return hus;
}
// 基于RGB颜色空间的阈值肤色识别,得到轮廓
vector<Point> findContour(Mat& src) {
Mat mask = Mat(src.rows, src.cols, CV_8U, Scalar(0));
for (int i = 0; i < src.rows; i++)
{
for (int j = 0; j < src.cols; j++)
{
int r, g, b;
r = src.at<Vec3b>(i, j)[2];
g = src.at<Vec3b>(i, j)[1];
b = src.at<Vec3b>(i, j)[0];
if (r > 95 && g > 40 && b > 20 && max(max(r, g), b) - min(min(r, g), b) > 15 && abs(r - g) > 15 && r > g && r > b)
{
mask.at<uchar>(i, j) = 255;
}
else if (r > 220 && g > 210 && b > 170 && abs(r - g) <= 15 && r > b && g < b)
{
mask.at<uchar>(i, j) = 255;
}
}
}
Mat ele = getStructuringElement(MORPH_RECT, Size(9, 9));
morphologyEx(mask, mask, MORPH_CLOSE, ele);
vector<vector<Point>> contours;
findContours(mask, contours, RETR_EXTERNAL, CHAIN_APPROX_NONE);
int max_idx = 0; double max_area = 0.0;
for (size_t i = 0; i < contours.size(); i++)
{
double area = contourArea(contours[i]);
if (max_area < area) {
max_area = area;
max_idx = i;
}
}
drawContours(mask, contours, max_idx, Scalar(255), -1);
imshow("mask", mask);
waitKey(100);
return contours[max_idx];
}
// 将描述子保存在本地
void generateTrainData(string& trainImgPath) {
vector<string> filenames;
glob(trainImgPath, filenames);
string s = trainImgPath.substr(trainImgPath.length() - 2, trainImgPath.length() - 1);
for (int n = 0; n < filenames.size(); n++) {
Mat src = imread(filenames[n]);
resize(src, src, Size(1000, 1000));
vector<Point> contour = findContour(src);
//vector<double> des = FourierShapeDescriptors(contour, 16);
//vector<double> des = huDescriptors(contour);
vector<double> des = FourierShapeDescriptors(contour);
string txtPath = "./train1/" + s + "_" + to_string(n) + ".txt";
ofstream file(txtPath);
for (size_t i = 0; i < des.size(); i++)
{
file << des[i] << endl;
}
file.close();
}
}
// 输入图像,获得预测值
int predict(Mat& src)
{
int dim = n_dims;
vector<Point> contour = findContour(src);
//vector<double> des = huDescriptors(contour);
vector<double> des = FourierShapeDescriptors(contour);
Ptr<SVM> svm = StatModel::load<SVM>("./svm.xml");
Mat sample = Mat(1, dim, CV_32FC1);
float* p = sample.ptr<float>();
for (int i = 0; i < dim; i++)
{
p[i] = des[i];
}
Mat result;
svm->predict(sample, result);
int pred = int(result.at<float>(0) + 0.5);//四舍五入
return pred;
}
// 训练svm
void train(string& trainTxtPath) {
//加载训练数据及标签
Mat train_data = Mat::zeros(n_samples * n_class, n_dims, CV_32FC1);//每一行是一个训练样本,每一列是特征
Mat train_label = Mat::zeros(n_samples * n_class, 1, CV_32FC1);//标签
for (int i = 0; i < n_class; i++)
{
for (int j = 0; j < n_samples; j++)
{
int num = i * n_samples + j;
string filename = "train1/" + to_string(i) + "_" + to_string(j) + ".txt";
ifstream file(filename);
int k = 0;
if (file.is_open()) {
string line;
while (getline(file, line)) {
double d = stod(line);
train_data.at<float>(num, k) = d;
k++;
}
file.close();
}
train_label.at<float>(num, 0) = i;
}
}
//训练
Ptr<SVM> svm = SVM::create();
svm->setType(SVM::NU_SVR);//回归算法
svm->setKernel(SVM::KernelTypes::RBF);//设置核函数
svm->setC(8);
svm->setGamma(1.0/ n_dims);
svm->setNu(0.5);
svm->setTermCriteria(TermCriteria(TermCriteria::EPS | TermCriteria::MAX_ITER, 500000, 0.0001));
svm->train(train_data, ROW_SAMPLE, train_label);
svm->save("./svm.xml");
}
int main() {
// 生成数据
for (int n = 0; n < n_class; n++) {
string trainImgPath = "./石头剪刀布/"+to_string(n);
generateTrainData(trainImgPath);
}
// 训练
string trainTxtPath = "./";
train(trainTxtPath);
vector<string> filenames;
glob("./石头剪刀布/test", filenames);
// 测试
for (int n = 0; n < filenames.size(); n++) {
string filename = filenames[n];
int idx = filename.find_last_of("-");
string c = filename.substr(idx-1, idx);
Mat src = imread(filename);
resize(src, src, Size(1000, 1000));
int pred = predict(src);
cout << "label:" << c[0] << ", predict:" << pred << endl;
}
return 0;
}
2.2 检测液位
生产瓶装工业化学品的一家公司雇用你设计一种方法来检测未装满产品的瓶子。传送带上的瓶子经过自动灌装和封盖站时如右图所示。液位低于瓶颈底部和肩部之间的中点时,就认为瓶子未完全装满。肩部是瓶子侧面与瓶子倾斜部分的交点。瓶子的移动速度很快,但公司有个成像系统,这个系统的前端安装有照明闪光灯,它能有效地停止瓶子的移动,因此可以得到下方显示的样本图像。根据你掌握的知识,给出一种检测瓶子为装满的方案。详细说明可能会影响你的方案的假设。
 随便写的,好像和本章没啥关系...
随便写的,好像和本章没啥关系...
#include <opencv2/opencv.hpp>
using namespace cv;
using namespace std;
int findMaxContour(Mat& binImg, vector<vector<Point>>& contours) {
findContours(binImg, contours, RETR_EXTERNAL, CHAIN_APPROX_SIMPLE);
int max_idx = 0; double max_area = 0.0;
for (size_t i = 0; i < contours.size(); i++)
{
double area = contourArea(contours[i]);
if (max_area < area) {
max_area = area;
max_idx = i;
}
}
return max_idx;
}
void horizonHist(Mat& inputMat, vector<int>& hist) {
for (int row = 0; row < inputMat.rows; row++) {
int sum = 0;
for (int col = 0; col < inputMat.cols; col++) {
if ((int)inputMat.at<uchar>(row, col) > 0)
sum++;
}
hist.push_back(sum);
}
}
void findKeyPoints(vector<int>& hist, int max, vector<int>& keyPoints) {
int neck = -1, shoulder = -1, count = 0, i = 30;
for (; i < 200; i++) {
if (hist[i + 1] > hist[i]) {
if (count == 0)
neck = i;
count++;
}
else {
count = 0;
}
if (count == 3)
break;
}
keyPoints.push_back(neck);
for (; i < 200; i++) {
if ((hist[i + 2] - hist[i-1])<2&& hist[i]>max*0.95) {
if (count == 0)
shoulder = i;
count++;
}
else {
shoulder = -1;
count = 0;
}
if (count == 3)
break;
}
keyPoints.push_back(shoulder);
}
int main() {
Mat src = imread("./习题.tif", 0);
Mat binImg, binImg1, markImg;
cvtColor(src, markImg, COLOR_GRAY2BGR);
threshold(src, binImg, 10, 255, THRESH_BINARY);
threshold(src, binImg1, 200, 255, THRESH_BINARY);
vector<vector<Point>> contours;
findContours(binImg, contours, RETR_EXTERNAL, CHAIN_APPROX_SIMPLE);
vector<Rect> bottleRects;
for (size_t i = 0; i < contours.size(); i++)
{
Rect r = boundingRect(contours[i]);
if (r.height > src.rows * 0.9)
bottleRects.push_back(r);
}
for (size_t i = 0; i < bottleRects.size(); i++)
{
Mat binRoi, binRoi1;
Rect r = bottleRects[i];
Mat bottleRoi = src(Rect(r.tl().x, 0, r.width, src.rows));
threshold(bottleRoi, binRoi, 10, 255, THRESH_BINARY);
threshold(bottleRoi, binRoi1, 210, 255, THRESH_BINARY);
Mat ele = getStructuringElement(MORPH_RECT, Size(11, 1));
morphologyEx(binRoi1, binRoi1, MORPH_OPEN, ele);
int idx = findMaxContour(binRoi1, contours);
Rect r1 = boundingRect(contours[idx]);
int waterLine = r1.br().y;
vector<int> hist;
horizonHist(binRoi, hist);
Mat dst = Mat::zeros(r.width, src.rows, CV_8UC3);
for (int i = 0; i < src.rows; i++) {
int h = hist[i];
if (h > 0)
rectangle(dst, Rect(i, r.width - h, 1, h), Scalar(255, 255, 255), -1);
}
vector<int> keyPoints;
findKeyPoints(hist, r.width, keyPoints);
line(markImg, Point(r.tl().x, keyPoints[0]), Point(r.br().x, keyPoints[0]), Scalar(0, 255, 0), 1);
line(markImg, Point(r.tl().x, keyPoints[1]), Point(r.br().x, keyPoints[1]), Scalar(0, 255, 0), 1);
int line_standard = (keyPoints[1] + keyPoints[0]) / 2;
line(markImg, Point(r.tl().x, line_standard), Point(r.br().x, line_standard), Scalar(0, 255, 0), 1);
Scalar s;
if (waterLine< line_standard + 3 && waterLine > line_standard - 3)
s = Scalar(255, 0, 0);
else
s = Scalar(0, 0, 255);
line(markImg, Point(r.tl().x, waterLine), Point(r.br().x, waterLine), s, 1);
}
waitKey(0);
return 0;
}

参考:
1. 冈萨雷斯《数字图像处理(第四版)》Chapter 11(所有图片可在链接中下载)
3. opencv手势识别


 浙公网安备 33010602011771号
浙公网安备 33010602011771号