斜率优化（凸壳优化）和李超线段树

前言

闲话

写了好久，有些细节点理解了，但是总是写不出来，不知道怎么解释，多感性理解吧，自己多画图辅助理解。

其实在很多事情上，可能放弃才是正确的选择。

能想清楚就行，不必强求自己。像我一直困在一个点想来想去，花了不少时间，最后还是只能笼统地概括...

标记永久化

解释

线段树中普通的区间修改都需要懒标记，但懒标记的维护要及时更新下传，为了避免多次无意义的下传操作，就要用到标记永久化。

举个简单例子，线段树的区间加，查询区间最大值：

常见的方法就是在区间修改的时候维护一个标记，表示区间被加的值，当访问到这个区间时，标记就会被下传；

而标记永久化的区别就在于，懒标记不会下传，将会永久保留在当前节点上，那么在查询的时候，\(\text{得到的最大值 = 真实的最大值 - 当前节点的标记值}\)，计算答案时只需要将当前的标记值一并算入即可。

要求

不同的修改操作是可以交换顺序的，或者对答案的贡献是独立的，不适用于像既有乘法又有加法的区间操作。

复杂度分析

由于标记不需要下传，只需要合并，每个点至多一个标记，查询时最多考虑 \(\log{n}\) 个标记，复杂度为 \(O(n\log{n})\)。

李超线段树

闲话

暑假多校训练中听到一句关于李超线段树本质的话：

王侯将相宁有种乎。

前置

线段树
标记永久化

引入

【模板】李超线段树 / [HEOI2013] Segment

加入一个一次函数，定义域为 \([l,r]\)；
给定 \(k\)，求定义域包含 \(k\) 的所有一次函数中，在 \(x = k\) 处取值最大的那个，如果有多个函数取值相同，选编号最小的。

注意：当线段垂直于 \(x\) 轴时，会出现除以零的情况。假设线段两端点分别为 \((x,y_0)\) 和 \((x,y_1)\)，\(y_0 < y_1\)，则插入定义域为 \([x,x]\) 的一次函数 \(f(x)=0 \cdot x+y_1\)。

我们发现，传统的线段树无法很好地维护这样的信息。这种情况下，李超线段树便应运而生。

过程

显然任意两条在区间 \([l,r]\) 上的线段之间只会有两种状态：相交或覆盖。

发现无论如何，总有一条线段在至少一个半区间上是完全优于另一条线段的；

定义【完全覆盖】为在一段区间 \([l,r]\) 内某条线段完全优于其他的线段。

如下图：线段 \(f\) 在区间 \([3,6]\) 上完全覆盖。

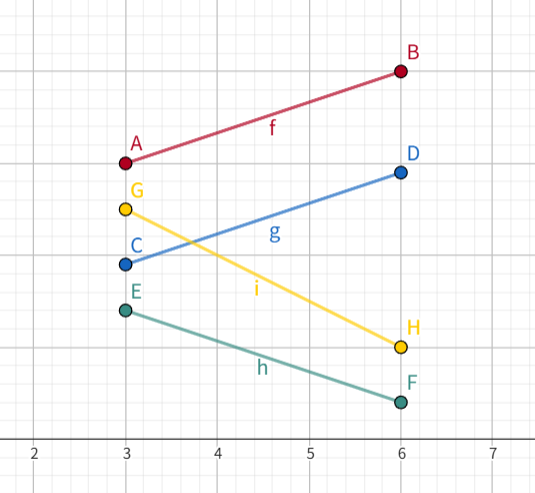
那么就给了我们一个思路，尝试建立线段树去维护在 \([l,r]\) 区间上（设区间的中点为 \(m\)）的所有线段中，在左区间 \([l,m]\) 或右区间 \([m+1,r]\) 中的至少一个区间上完全覆盖的线段的编号。

现在考虑加入一条新的直线对于区间 \([l,r]\) 的贡献：

注：\(f,g\) 分别是新加入的线段和原标记最优的线段。

如图，按新线段 \(f\) 取值是否大于原标记线段 \(g\)，我们可以把当前区间分为两个子区间。其中肯定有一个子区间被左区间或右区间完全包含，也就是说，在两条线段中，肯定有一条线段，只可能成为左区间的答案，或者只可能成为右区间的答案。

我们用这条线段递归更新对应子树，用另一条线段作为懒标记更新整个区间，这就保证了递归下传的复杂度。

当一条线段只可能成为左或右区间的答案时，才会被下传，所以不用担心漏掉某些线段。

如果新线段 \(f\) 更优，则将 \(f\) 和 \(g\) 交换，使线段在中点 \(x = m\) 处交换后的 \(f\) 不优于 \(g\)（下面所有的 \(f\) 和 \(g\) 都是交换过后的）：

①. 若左端点处 \(f\) 更优，说明 \(f\) 和 \(g\) 在左半区间 \([l,m]\) 产生了交点，则递归到左儿子中下传信息；
②. 若右端点处 \(f\) 更优，说明 \(f\) 和 \(g\) 在右半区间 \([m + 1,r]\) 产生了交点，则递归到右儿子中下传信息；
③. 若左右端点处 \(g\) 都更优，说明 \(g\) 在区间 \([l,r]\) 完全覆盖 \(f\)，不需要继续下传。

若 \(f\) 和 \(g\) 刚好交于中点，在实现中可以归入中点处 \(f\) 不如 \(g\) 优的情况，会往 \(f\) 更优的一个端点进行递归下传。

inline void upd(int rt,int l,int r,int x) {
	int mid=(l+r)>>1;
	int &y=rd[rt];
	int tp=cmp(calcY(x,mid),calcY(y,mid));
	if(tp==1||(!tp&&x<y))
		swap(x,y);
	int tl=cmp(calcY(x,l),calcY(y,l));
	int tr=cmp(calcY(x,r),calcY(y,r));
	if(tl==1||(!tl&&x<y))
		upd(lson,l,mid,x);
	if(tr==1||(!tr&&x<y))
		upd(rson,mid+1,r,x);
	return ;
}

最后查询的时候运用标记永久化思想，将路径上所有的标记都作比较求极值即可。

闲话：我在这想了好几天，卡在这，只能感性理解，没法给出严谨的证明为什么需要标记永久化，太弱了qwq

复杂度分析：

加入线段时，区间修改打懒标记要 \(O(n\log{n})\)，除此之外在每个标记的点都需要递归下传最多 \(\log{n}\) 层，所以插入操作的时间复杂度为 \(O(n\log^2{n})\)。

查询时的标记永久化的使用就显得非常巧妙了_(¯▽¯)，复杂度为 \(O(n\log{n})\)。

总体的复杂度为 \(O(n\log^2{n})\)，瓶颈在加入线段操作的 \(O(n\log^2{n})\)。

特别的，加入的是直线的话，复杂度就变为 \(O(n\log{n})\)，因为每条直线只用在 \([1,N]\) 打一次懒标记。

局限性：只能支持单点查询。

Code

#include<bits/stdc++.h>
#define int long long
#define lson rt<<1
#define rson rt<<1|1
#define M(x,y) make_pair(x,y)
using namespace std;
typedef pair<double,int> pdl;
const double eps=1e-9;
const int mod1=39989;
const int mod2=1e9;
const int N=1e5+10;
int n;
struct Line {
	double k,b;
} p[N];
int cnt,rd[N<<2];
inline int cmp(double x,double y) {
	if(x-y>eps)
		return 1;
	if(y-x>eps)
		return -1;
	return 0;
}
inline double calcY(int id,int x) {
	return p[id].b+p[id].k*x;
}
inline void add(int x0,int y0,int x1,int y1) {
	++cnt;
	if(x0==x1) {
		p[cnt].k=0;
		p[cnt].b=max(y0,y1);
	} else {
		p[cnt].k=1.0*(y1-y0)/(x1-x0);
		p[cnt].b=y0-p[cnt].k*x0;
	} 
	return ;
}
inline void upd(int rt,int l,int r,int x) {
	int mid=(l+r)>>1;
	int &y=rd[rt];
	int tp=cmp(calcY(x,mid),calcY(y,mid));
	if(tp==1||(!tp&&x<y))
		swap(x,y);
	int tl=cmp(calcY(x,l),calcY(y,l));
	int tr=cmp(calcY(x,r),calcY(y,r));
	if(tl==1||(!tl&&x<y))
		upd(lson,l,mid,x);
	if(tr==1||(!tr&&x<y))
		upd(rson,mid+1,r,x);
	return ;
}
inline void update(int rt,int l,int r,int s,int t,int x) {
	if(s<=l&&r<=t) {
		upd(rt,l,r,x);
		return ;
	}
	int mid=(l+r)>>1;
	if(s<=mid) update(lson,l,mid,s,t,x);
	if(mid<t) update(rson,mid+1,r,s,t,x);
	return ;
}
inline pdl pmax(pdl x,pdl y) {
	if(cmp(x.first,y.first)==1)
		return x;
	if(cmp(x.first,y.first)==-1)
		return y;
	if(x.second<y.second)
		return x;
	return y;
}
inline pdl query(int rt,int l,int r,int x) {
	if(l>x||r<x)
		return M(0,0);
	double res=calcY(rd[rt],x);
	if(l==r)
		return M(res,rd[rt]);
	int mid=(l+r)>>1;
	return pmax(M(res,rd[rt]),pmax(query(lson,l,mid,x),query(rson,mid+1,r,x)));
}
signed main() {
	scanf("%lld",&n);
	int lastans=0;
	while(n--) {
		int op;
		scanf("%lld",&op);
		if(op==1) {
			int x0,y0,x1,y1;
			scanf("%lld%lld%lld%lld",&x0,&y0,&x1,&y1);
			x0=(x0+lastans-1+mod1)%mod1+1;
			x1=(x1+lastans-1+mod1)%mod1+1;
			y0=(y0+lastans-1+mod2)%mod2+1;
			y1=(y1+lastans-1+mod2)%mod2+1;
			if(x0>x1)
				swap(x0,x1),swap(y0,y1);
			add(x0,y0,x1,y1);
			update(1,1,mod1,x0,x1,cnt);
		} else {
			int x;
			scanf("%lld",&x);
			x=(x+lastans-1+mod1)%mod1+1;
			lastans=query(1,1,mod1,x).second;
			printf("%lld\n",lastans);
		}
	}
	return 0;
}

斜率优化/凸壳优化

引入

简要：有 \(n\) 个数，现在把其分割成若干组，每组代价的贡献是这组内所有数的和的平方加上常数 \(m\)，求最小的代价。

解析

直入主题，现在有 \(O(n^2)\) 的转移式子，如下：

\(f_i = min \{ f_j + ( g_i - g_j ) ^ 2 + m \},0 < j < i\)

其中 \(f_i\) 表示前 \(i\) 个数的代价的最小值，\(g_i\) 表示前 \(i\) 个数字的和。

拿到这种复杂的转移式子，先尝试展开，看是否能套用 \(y = kx + b\) 的斜率优化 DP 的标准形式，从而优化到 \(O(n)\) 或者 \(O(nlogn)\)：

\(f_i = f_j + g_i ^ 2 + g_j ^ 2 - 2g_ig_j + m\)

移项可得：

\(f_j + g_j ^ 2 = 2g_ig_j + f_i - g_i ^ 2 - m\)

对照 \(y = kx + b\)，可得：

\( \begin{align*} y &= f_j + g_j ^ 2 \\ x &= 2g_j \\ k &= g_i \\ b &= f_i - g_i ^ 2 - m \end{align*} \)

（这里其实 \(x\) 也可以为 \(g_j\)，则 \(k\) 为 \(2g_i\)）

本转移式中：

\(y\) 只与 \(j\) 有关；
\(x\) 只与 \(j\) 有关，且随着 \(j\) 递增而递增；
\(k\) 只与 \(i\) 有关，且随着 \(i\) 递增而递增；
\(b\) 只与 \(i\) 有关，且包含 \(f_i\)。

由于 \(x,k\) 都具有单调性，可以使用单调队列维护。

单调队列

例题：[HNOI2008] 玩具装箱和[APIO2010] 特别行动队

Solution

（最近做的是【特别行动队】，比较熟悉，就那这题作例）

按道理，考虑暴力转移：

\(f_i = max \{ f_j + a( g_i - g_j ) ^ 2 + b( g_i - g_j ) + c \},0 < j < i\)

展开并移项可得：

\(f_j + ag_j ^ 2 - bg_j = 2ag_ig_j + f_i - ag_i ^ 2 - bg_i - c\)

令：

\( \begin{align*} y &= f_j + ag_j ^ 2 - bg_j \\ x &= 2ag_j \\ k &= g_i \\ b &= f_i - ag_i ^ 2 - bg_i - c \end{align*} \)

注意：本题的 \(a < 0\)，后面会讲到。

发现 \(x,k\) 都是单调递增的，用单调队列。

inline int Y(int i) {
	return f[i]+a*g[i]*g[i]-b*g[i];
}
inline int X(int i) {
	return 2*a*g[i];
}
inline int slopeU(int i,int j) {
	return Y(j)-Y(i);
}
inline int slopeD(int i,int j) {
	return X(j)-X(i);
}

【凸壳】大白话来讲就是所有 \((x_i,y_i)\) 的点对中最外一层包围的点。

接下来是做题的一般性做题步骤：

Step 1

取两个决策点 \(j1\) 和 \(j2\)，使得 \(j2\) 优于 \(j1\)，即：

\(f_{j1} + ag_i ^ 2 + ag_{j1} ^ 2 - 2ag_ig_{j1} + bg_i - bg_{j1} + c \le f_{j2} + ag_i ^ 2 + ag_{j2} ^ 2 - 2ag_ig_{j2} + bg_i - bg_{j2} + c\)

消掉同项：

\(f_{j1} + ag_{j1} ^ 2 - 2ag_ig_{j1} - bg_{j1} \le f_{j2} + ag_{j2} ^ 2 - 2ag_ig_{j2} - bg_{j2}\)

移项：

\(2ag_i(g_{j2} - g_{j1}) \le f_{j2} + ag_{j2} ^ 2 - bg_{j2} - ( f_{j1} + ag_{j1} ^ 2 - bg_{j1} )\)

因为 \(a < 0,g_{j2} - g_{j1} < 0\)，所以 \(2a(g_{j2} - g_{j1}) > 0\)，不用变号：

\(g_i \le \frac{f_{j2} + ag_{j2} ^ 2 - bg_{j2} - ( f_{j1} + ag_{j1} ^ 2 - bg_{j1} )}{2ag_{j2} - 2ag_{j1}}\)

即 \(g_i \le \frac{y_{j2} - y_{j1}}{x_{j2} - x_{j1}}\)

这个就是第一个条件。

while(head+1<=tail&&slopeU(q[head],q[head+1])>=g[i]*slopeD(q[head],q[head+1]))
	++head;

注意：为了避免精度问题，采用乘法。

Step 2

其实实质就是，当遍历到 \(i\) 时，斜率为 \(k = g_i\) 直线慢慢接近凸壳，知道碰到第一个点，这个点必然就是当前维护的凸壳队列上的一个点。

第二个我们需要确定其凸壳的图像，\(x = 2ag_j\) 单调递减，\(k = g_i\) 单调递增，所以大致得出图像：

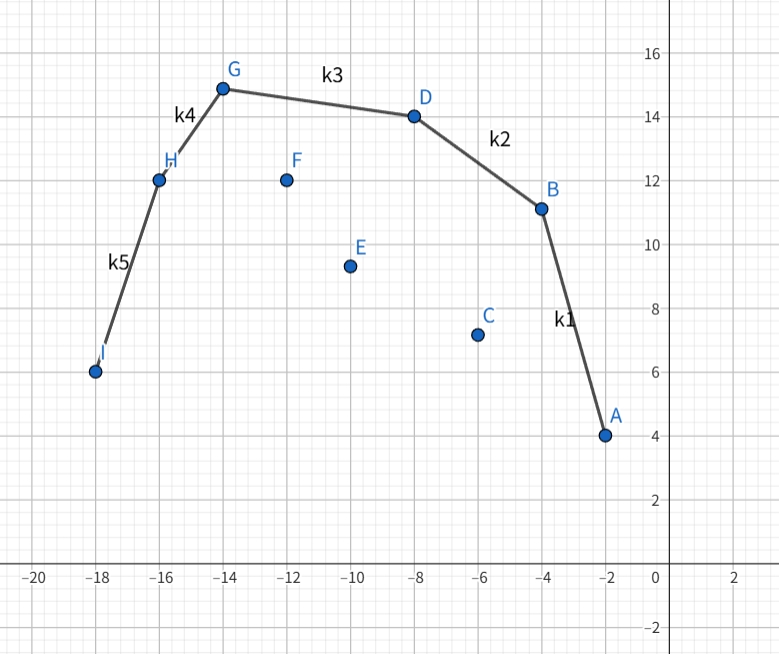
由性质可知 \(k1 < k2 < k3 < k4 < k5\)，所以队列的队尾的斜率是越来越大的，得到第二个条件。

while(head+1<=tail&&slopeU(q[tail-1],q[tail])*slopeD(q[tail],i)>=slopeU(q[tail],i)*slopeD(q[tail-1],q[tail]))
	--tail;

这里要提一个点，这里特殊的在于 \(a < 0\)，所以像【引入】中提到的 \(x,k\) 中的常数项可以互相转化的情况不能直接搬用，需要细细考虑：

当 \(x = g_j , k = 2ag_i\) 时，\(x\) 是单调递增，而 \(k\) 是单调递减。

【Step 1】：

\(2ag_i(g_{j2} - g_{j1}) \le f_{j2} + ag_{j2} ^ 2 - bg_{j2} - ( f_{j1} + ag_{j1} ^ 2 - bg_{j1} )\)

此时 \(g_{j2} - g_{j1} > 0\)，也不需要变号：

\(2ag_i \le \frac{y_{j2} - y_{j1}}{x_{j2} - x_{j1}}\)

while(head+1<=tail&&slopeU(q[head],q[head+1])>=2*a*g[i]*slopeD(q[head],q[head+1]))
	++head;

【Step 2】：

凸壳的图像变成：

此时 \(k1 > k2 > k3 > k4 > k5\)，说明队尾的斜率是越来越小的。

while(head+1<=tail&&slopeU(q[tail-1],q[tail])*slopeD(q[tail],i)<=slopeU(q[tail],i)*slopeD(q[tail-1],q[tail]))
	--tail;

注意观察和上面第一种取法的区别。

还需要注意的是在程序中若 \(f_0\) 不为 \(0\)，初始也需要把其加入凸壳的队列中，平常最好有没有都加，养成好习惯！！！

Code1

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e6+10;
int n,a,b,c,p[N];
int f[N],g[N];
int q[N],head=1,tail;
inline int Y(int i) {
	return f[i]+a*g[i]*g[i]-b*g[i];
}
inline int X(int i) {
	return 2*a*g[i];
}
inline int slopeU(int i,int j) {
	return Y(j)-Y(i);
}
inline int slopeD(int i,int j) {
	return X(j)-X(i);
}
signed main() {
	scanf("%lld%lld%lld%lld",&n,&a,&b,&c);
	for(int i=1;i<=n;i++) {
		scanf("%lld",&p[i]);
		g[i]=g[i-1]+p[i];
	}
	memset(f,0xcf,sizeof f);
	f[0]=0,q[++tail]=0;
	for(int i=1;i<=n;i++) {
		while(head+1<=tail&&slopeU(q[head],q[head+1])>=g[i]*slopeD(q[head],q[head+1]))
			++head;
		int j=q[head];
		int x=g[i]-g[j];
		f[i]=max(f[j]+a*x*x+b*x+c,f[i]);
		while(head+1<=tail&&slopeU(q[tail-1],q[tail])*slopeD(q[tail],i)>=slopeU(q[tail],i)*slopeD(q[tail-1],q[tail]))
			--tail;
		q[++tail]=i;
	}
	printf("%lld\n",f[n]);
	return 0;
}

Code2

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e6+10;
int n,a,b,c,p[N];
int f[N],g[N];
int q[N],head=1,tail;
inline int Y(int i) {
	return f[i]+a*g[i]*g[i]-b*g[i];
}
inline int X(int i) {
	return g[i];
}
inline int slopeU(int i,int j) {
	return Y(j)-Y(i);
}
inline int slopeD(int i,int j) {
	return X(j)-X(i);
}
signed main() {
	scanf("%lld%lld%lld%lld",&n,&a,&b,&c);
	for(int i=1;i<=n;i++) {
		scanf("%lld",&p[i]);
		g[i]=g[i-1]+p[i];
	}
	memset(f,0xcf,sizeof f);
	f[0]=0,q[++tail]=0;
	for(int i=1;i<=n;i++) {
		while(head+1<=tail&&slopeU(q[head],q[head+1])>=2*a*g[i]*slopeD(q[head],q[head+1]))
			++head;
		int j=q[head];
		int x=g[i]-g[j];
		f[i]=max(f[j]+a*x*x+b*x+c,f[i]);
		while(head+1<=tail&&slopeU(q[tail-1],q[tail])*slopeD(q[tail],i)<=slopeU(q[tail],i)*slopeD(q[tail-1],q[tail]))
			--tail;
		q[++tail]=i;
	}
	printf("%lld\n",f[n]);
	return 0;
}

李超线段树优化

[CEOI 2017] Building Bridges

前置知识

李超线段树
离散化

Solution

设 \(f_i\) 表示连接前 \(i\) 根柱子的最小代价，\(g_i\) 表示拆除前 \(i\) 根柱子的代价，前缀和维护区间拆除柱子所需的代价，由此可以列出转移方程式：

\(f_i = min \{ f_j + (h_i - h_j) ^ 2 + (g_{i-1} - g_j) \},0 < j < i\)

同样的，看到复杂的转移式，直接展开并得到：

\(f_j + h_j ^ 2 - g_j = 2h_ih_j + f_i - h_i ^ 2 - g_{i-1}\)

按照普遍的斜率优化思路把其转化为 \(y = kx + b\) 的形式：

\( \begin{align*} y &= f_j + h_j ^ 2 - g_j \\ x &= 2h_j \\ k &= h_i \\ b &= f_i - h_i ^ 2 - g_{i-1} \end{align*} \)

发现 \(x,k\) 都不具有单调性，故不能使用单调队列维护。

重新展开得到：

\(f_i - h_i ^ 2 - g_{i-1} = -2h_ih_j + f_j + h_j ^ 2 - g_j\)

转化成：

\( \begin{align*} y &= f_i - h_i ^ 2 - g_{i-1} \\ x &= h_i \\ k &= -2h_j \\ b &= f_j + h_j ^ 2 - g_j \end{align*} \)

\(k,b,x\) 都已知，\(y\) 只与 \(i\) 有关，且包含 \(f_i\)，\(f_i\) 要取最小值，转换为：

有用 \(k_j,b_j\) 表示的 \(i-1\) 条直线 \(j\)，求所有直线在 \(x\) 处最小的 \(y\) 的取值。

那不妥妥地用李超线段树维护啊，最后需要注意值域过大时要离散化。

Code

#include<bits/stdc++.h>
#define int long long
#define lson rt<<1
#define rson rt<<1|1
#define M(x,y) make_pair(x,y)
using namespace std;
typedef pair<double,int> pdl;
const double inf=1e18;
const double eps=1e-9;
const int N=1e5+10;
int n,h[N],w[N],s[N];
int unq[N],uh[N],f[N];
struct Line {
	double k,b;
} l[N];
int cnt,rd[N*4];
inline int cmp(double x,double y) {
	if(x-y>eps)
		return 1;
	if(y-x>eps)
		return -1;
	return 0;
}
inline double calcY(int id,int x) {
	if(id==0) return inf;
	return l[id].b+l[id].k*x;
}
inline void upd(int rt,int l,int r,int x) {
	int mid=(l+r)>>1;
	int &y=rd[rt];
	int tp=cmp(calcY(x,unq[mid]),calcY(y,unq[mid]));
	if(tp==-1||(!tp&&x<y))
		swap(x,y);
	int tl=cmp(calcY(x,unq[l]),calcY(y,unq[l]));
	int tr=cmp(calcY(x,unq[r]),calcY(y,unq[r]));
	if(tl==-1||(!tl&&x<y))
		upd(lson,l,mid,x);
	if(tr==-1||(!tr&&x<y))
		upd(rson,mid+1,r,x);
	return ;
}
inline void update(int rt,int l,int r,int s,int t,int x) {
	if(s<=l&&r<=t) {
		upd(rt,l,r,x);
		return ;
	}
	int mid=(l+r)>>1;
	if(s<=mid) update(lson,l,mid,s,t,x);
	if(mid<t) update(rson,mid+1,r,s,t,x);
	return ;
}
inline pdl pmin(pdl x,pdl y) {
	if(cmp(x.first,y.first)==-1)
		return x;
	if(cmp(x.first,y.first)==1)
		return y;
	if(x.second<y.second)
		return x;
	return y;
}
inline pdl query(int rt,int l,int r,int x) {
	if(l>x||r<x)
		return M(inf,0);
	double res=calcY(rd[rt],unq[x]);
	if(l==r)
		return M(res,rd[rt]);
	int mid=(l+r)>>1;
	return pmin(M(res,rd[rt]),pmin(query(lson,l,mid,x),query(rson,mid+1,r,x)));
}
signed main() {
	scanf("%lld",&n);
	for(int i=1;i<=n;i++) {
		scanf("%lld",&h[i]);
		unq[i]=h[i];
	}
	for(int i=1;i<=n;i++) {
		scanf("%lld",&w[i]);
		s[i]=s[i-1]+w[i];
	}
	sort(unq+1,unq+n+1);
	int m=unique(unq+1,unq+n+1)-unq-1;
	for(int i=1;i<=n;i++)
		uh[i]=lower_bound(unq+1,unq+m+1,h[i])-unq;
	for(int i=1;i<=n;i++) {
		if(i!=1) {
			pdl p=query(1,1,m,uh[i]);
			int j=p.second;
			f[i]=f[j]+(h[i]-h[j])*(h[i]-h[j])+(s[i-1]-s[j]);
		}
		++cnt;
		l[cnt].k=-2*h[i];
		l[cnt].b=f[i]+h[i]*h[i]-s[i];
		update(1,1,m,1,m,cnt);
	}
	printf("%lld\n",f[n]);
	return 0;
}

小总结

带大家理解一下单调队列和李超线段树在维护斜率优化时的不同。

单调队列/Splay维护

闲话：虽然我不怎么用 Splay...

实质：\(b = y - kx\)

\(x,y\) 只与 \(j\) 有关，且前面已经求出；

\(k\) 只与 \(i\) 有关且已知，\(b\) 只与 \(i\) 有关且包含 \(f_i\)，要求 \(f_i\) 的最值，就可以转换为：

找到一个点 \((x,y)\)，用斜率为 \(k\) 的直线切这个点得到与 \(y\) 轴的交点 \(b\) 的值最大/小，即最大/小截距。

与 \(x,k\) 的单调性都有关。

李超线段树维护

实质：\(y = kx + b\)

\(k,b\) 只与 \(j\) 有关，且前面已经求出；

\(x\) 只与 \(i\) 有关且已知，\(y\) 只与 \(i\) 有关且包含 \(f_i\)，要求 \(f_i\) 的最值，就可以转换为：

找到一条直线 \((k,b)\)，使得在 \(x\) 处得到 \(y\) 的值最大/小。

与 \(x,k\) 的单调性无关。

综上所述，看到转移式先展开，若 \(x,k\) 都具有单调性，直接单调队列暴力维护；否则全部套李超线段树即可。

如果学了其他的更好的优化方法，按题目的类型随机应变。

后记

可能有些的不足的地方，多多包涵！！！

特别鸣谢 & 部分内容的参考文献

posted @ 2025-07-14 11:03 Fireworks_Rise 阅读(15) 评论(0) 收藏举报

刷新页面返回顶部

Fireworks-Rise

GD OIer

斜率优化（凸壳优化）和李超线段树

前言

闲话

标记永久化

解释

要求

复杂度分析

李超线段树

闲话

前置

引入

过程

斜率优化/凸壳优化

引入

解析

单调队列

Solution

Step 1

Step 2

李超线段树优化

前置知识

Solution

小总结

单调队列/Splay维护

李超线段树维护

后记

特别鸣谢 & 部分内容的参考文献

公告