【最大子矩形】(悬线法,极大化思想)
前言
此乃小 Oler 的一篇算法随笔,从今日后,还会进行详细的修订。
注:本文可能会参考某些大佬的文献。
定义 & 说明
最大子矩形问题:在一个给定的矩形网格中有一些障碍点,要找出网格内部不包含任何障碍点,且边界与坐标轴平行的最大子矩形。
- 定义有效子矩形为内部不包含任何障碍点且边界与坐标轴平行的子矩形。如图所示,第一个是有效子矩形(尽管边界上有障碍点),第二个不是有效子矩形(因为内部含有障碍点)。
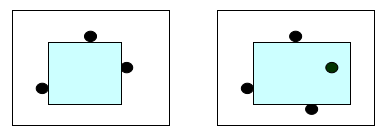
-
极大有效子矩形:一个有效子矩形,如果不存在包含它且比它大的有效子矩形,就称这个有效子矩形为极大有效子矩形。(为了叙述方便,以下称为极大子矩形)
-
定义最大有效子矩形为所有有效子矩形中最大的一个(或多个)。以下简称为最大子矩形。
——摘抄自文章《浅谈用极大化思想解决最大子矩形问题》
算法 No.1 (悬线法,递推思想)
定义
-
有效竖线:除了两个端点外,不覆盖任何障碍点的竖直线段。
-
悬线:上端点覆盖了一个障碍点或达到整个矩形上端的有效竖线。
如图所示的三个有效竖线都是悬线。
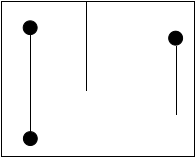
对于任何一个极大子矩形,它的上边界上要么有一个障碍点,要么和整个矩形的上边界重合。那么如果把一个极大子矩形按 \(x\) 坐标不同切割成多个(实际上是无数个)与 \(y\) 轴垂直的线段,则其中一定存在一条悬线。而且一条悬线通过尽可能地向左右移动恰好能得到一个子矩形(未必是极大子矩形,但只可能向下扩展)。
通过以上的分析,我们可以得到一个重要的定理:
-
【定理1】如果将一个悬线向左右两个方向尽可能移动所得到的有效子矩形称为这个悬线所对应的子矩形,那么所有悬线所对应的有效子矩形的集合一定包含了所有极大子矩形的集合。
-
注:【定理1】中的“尽可能”移动指的是移动到一个障碍点或者矩形边界的位置。
引入(Big Barn)
源自 洛谷 P2701 [USACO5.3] 巨大的牛棚 Big Barn
题目描述
农夫约翰想要在他的正方形农场上建造一座正方形大牛棚。他讨厌在他的农场中砍树,想找一个能够让他在空旷无树的地方修建牛棚的地方。我们假定,他的农场划分成 \(N \times N\) 的方格。输入数据中包括有树的方格的列表。你的任务是计算并输出,在他的农场中,不需要砍树却能够修建的最大正方形牛棚。牛棚的边必须和水平轴或者垂直轴平行。
EXAMPLE
考虑下面的方格,它表示农夫约翰的农场,‘.'表示没有树的方格,‘#'表示有树的方格
1 2 3 4 5 6 7 8
1 . . . . . . . .
2 . # . . . # . .
3 . . . . . . . .
4 . . . . . . . .
5 . . . . . . . .
6 . . # . . . . .
7 . . . . . . . .
8 . . . . . . . .
最大的牛棚是 \(5 \times 5\) 的,可以建造在方格右下角的两个位置其中一个。
输入格式
Line 1: 两个整数: \(N\) ( \(1 \le N \le 1000\) ),农场的大小,和 \(T\) ( \(1 \le T \le 10^4\) )有树的方格的数量。
Lines 2..T+1: 两个整数( \(1 \le x_i,y_i \le N\) ),,有树格子的横纵坐标。
输出格式
只由一行组成,约翰的牛棚的最大边长。
样例 #1
样例输入 #1
8 3
2 2
2 6
6 3
样例输出 #1
5
算法流程
初始化
\(up_{i,j}\) 表示对于以 \((i,j)\) 为底部的悬线的高度。
\(l_{i,j}\) 表示从悬线的底部 \((i,j)\) 开始,往左最多能移动到的位置的横坐标。
\(r_{i,j}\) 表示 \((i,j)\) 往右最多能移动到的位置的横坐标(碰到障碍点为止)。
\(res_{i,j}\) 表示当前点是否为障碍点。
注意:数组 \(l,r\) 表示的移动到的位置,而不是移动的步数。
对于任意一个点 \((i,j)\) ,都有 \(up_{i,j}=0\),\(l_{i,j}=j\),\(r_{i,j}=j\) 。
若 \((i,j)\) 为障碍点,则 \(res_{i,j}=1\) 。
这一步绝对不能忘了!!!
递推
以 \((i,j)\) 为底部的悬线分别往左右移动到的最远距离的位置为 \(l_{i,j}\) 和 \(r_{i,j}\) 。

状态转移方程式如下:
\(up_{i,j} \begin{cases} 0\\ up_{i-1,j}+1 \end{cases}\)
若当前为障碍点的时候,本身不能形成矩形,故把高度赋为 \(0\) ,
反之,其高度必定由上面的一个点 \((i-1,j)\) 的高度加 \(1\) 。
\(left_{i,j} = \max \begin{cases} left_{i-1,j}\\ left_{i,j-1} \end{cases}\)
由于我们需要求的是一个矩形,不可能出现矩形内的两行的起始点的纵坐标不同,而移动时不能越过障碍点,所以只能取两个中的最大值(由于 \(left{i,j}\) 记录的是坐标位置),如下图:
红色表示一条悬线的底部 \((3,4)\) ;
绿色表示从 \((3,3)\) 往左移动到最远位置的路径;
蓝色表示从 \((2,4)\) 往左移动到最远位置的路径;
橙色的方格表示障碍点。
其中数组 \(l\) 中存储的是最远位置的横坐标,即第二维。

\(right_{i,j} = \min \begin{cases} right_{i-1,j}\\ right_{i,j+1} \end{cases}\)
跟处理往左移动类似,不必过多诉说,只不过在取数时,应取其最小值。
如下图:
其中数组 \(r\) 中存储的是往右移动可达的最远位置的横坐标。

对于每个悬线的底部 \((i,j)\) ,取其中的最大边长,由于求得是正方形的边长,所以只用取高度 \(up_{i,j}\) 和左右之间的距离 \(r_{i,j}-l_{i,j}+1\) 中的最大值, 即\(ans=\max(ans,\min(r_{i,j}-l_{i,j}+1,up_{i,j}))\) ,最后输出 \(ans\) 即可。
这里多几嘴...此处依题目实际要求而定,如:求其面积,则为 \(r_{i,j}-l_{i,j}+1 \times up_{i,j}\) 。
Code(悬线)
#include<bits/stdc++.h>
using namespace std;
const int N=1001;
int n,m,x,y,ans,res[N][N];
int l[N][N],r[N][N],up[N][N];
int main() {
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) { //初始化
for(int j=1;j<=n;j++) {
l[i][j]=r[i][j]=j;
up[i][j]=1;
}
}
for(int i=1;i<=m;i++) { //标记障碍点
scanf("%d%d",&x,&y);
res[x][y]=1;
}
for(int i=1;i<=n;i++) { //预处理
for(int j=2;j<=n;j++) {
if(res[i][j]==0&&res[i][j-1]==0)
l[i][j]=l[i][j-1];
}
}
for(int i=1;i<=n;i++) {
for(int j=n-1;j>=1;j--) {
if(res[i][j]==0&&res[i][j+1]==0)
r[i][j]=r[i][j+1];
}
}
for(int i=1;i<=n;i++) { //左右移动悬线找出子矩形
for(int j=1;j<=n;j++) {
if(i>1&&res[i][j]==0&&res[i-1][j]==0) {
l[i][j]=max(l[i][j],l[i-1][j]);
r[i][j]=min(r[i][j],r[i-1][j]);
up[i][j]=up[i-1][j]+1;
}
ans=max(ans,min(r[i][j]-l[i][j]+1,up[i][j])); //求出最大子矩形
}
}
printf("%d\n",ans); //输出最大正方形的边长
return 0;
}
算法 No.2 (枚举法,极大化思想)
浅析极大化思想
-
【定理2】在一个有障碍点的矩形中的最大子矩形一定是一个极大子矩形。
-
证明:如果最大子矩形 \(A\) 不是一个极大子矩形,那么根据极大子矩形的定义,存在一个包含 \(A\) 且比 \(A\) 更大的有效子矩形,这与“ \(A\) 是最大子矩形”矛盾,所以定理成立。
例题引入(奶牛浴场)
题目源自 洛谷 P1578 奶牛浴场
题目描述
由于 John 建造了牛场围栏,激起了奶牛的愤怒,奶牛的产奶量急剧减少。为了讨好奶牛,John 决定在牛场中建造一个大型浴场。但是 John 的奶牛有一个奇怪的习惯,每头奶牛都必须在牛场中的一个固定的位置产奶,而奶牛显然不能在浴场中产奶,于是,John 希望所建造的浴场不覆盖这些产奶点。这回,他又要求助于 Clevow 了。你还能帮助 Clevow 吗?
John 的牛场和规划的浴场都是矩形。浴场要完全位于牛场之内,并且浴场的轮廓要与牛场的轮廓平行或者重合。浴场不能覆盖任何产奶点,但是产奶点可以位于浴场的轮廓上。
Clevow 当然希望浴场的面积尽可能大了,所以你的任务就是帮她计算浴场的最大面积。
输入格式
输入文件的第一行包含两个整数 \(L\) 和 \(W\),分别表示牛场的长和宽。
文件的第二行包含一个整数 \(n\),表示产奶点的数量。
以下 \(n\) 行每行包含两个整数 \(x\) 和 \(y\),表示一个产奶点的坐标。
所有产奶点都位于牛场内,即:\(0 \le x \le L\),\(0 \le y \le W\) 。
输出格式
输出文件仅一行,包含一个整数 \(S\),表示浴场的最大面积。
样例 #1
样例输入 #1
10 10
4
1 1
9 1
1 9
9 9
样例输出 #1
80
提示
对于所有数据,\(0 \le n \le 5 \times 10^3\),\(1 \le L,W \le 3 \times 10^4\) 。
流程
定理
-
【定理2】:一个极大子矩形的四条边一定都不能向外扩展。更进一步地说,一个有效子矩形是极大子矩形的充要条件是这个子矩形的每条边要么覆盖了一个障碍点,要么与整个矩形的边界重合。
-
证明:正确性很显然,如果一个有效子矩形的某一条边既没有覆盖一个障碍点,又没有与整个矩形的边界重合,那么肯定存在一个包含它的有效子矩形。
实现过程
-
把矩形左上,左下,右上,右下四个边界点设为障碍点;
-
求出所有的极大子矩形有两种情况:
①. 左边界与整个矩形的左边界重合,而右边界覆盖了一个障碍点
定义:
\(up\) 表示当前极大子形阵中 \(y\) 坐标的上界;
\(down\) 表示当前极大子矩行中 \(y\) 坐标的下界。
并记录以 \(up-down\) 为高,\(x_2-x_2\) 为宽的子矩形的面积,更新 \(up\) 和 \(down\)。
先枚举极大子矩形的左边界,然后从左到右依次扫描每一个障碍点,并不断修改可行的上下边界,从而枚举出所有以这个定点为左边界的极大子矩形。
由于第一次正序遍历只对左边界的部分求极大子矩形,而可能会因若干个障碍点而忽略了小部分右边的子矩形,所以可以用类似的方法从右到左扫描每一个点作为右边界的情况,反过来再处理一次。
②. 左右边界均与整个矩形的左右边界重合
按 \(y\) 轴对障碍点排序:
对每两个障碍点之间的极大子矩形取出最大子矩形的面积 \(ans\) 即可。
Code 2
#include<bits/stdc++.h>
using namespace std;
const int N=3e4+10;
struct Node {
int x,y;
}a[N];
int l,w,n,ans;
bool cmp(Node u,Node v) { //障碍点集合按x轴从小到大排序
return u.x<v.x;
}
bool cmp2(Node u,Node v) { //障碍点集合按y轴从小到大排序
return u.y<v.y;
}
int main() {
scanf("%d%d%d",&l,&w,&n);
for(int i=1;i<=n;i++)
scanf("%d%d",&a[i].x,&a[i].y);
a[++n].x=0,a[n].y=0;
a[++n].x=0,a[n].y=w;
a[++n].x=l,a[n].y=0;
a[++n].x=l,a[n].y=w; //添加四个边界点为障碍点
sort(a+1,a+n+1,cmp);
for(int i=1;i<=n;i++) {
int down=0,up=w; //上下边界
for(int j=i+1;j<n;j++) {
ans=max(ans,(a[j].x-a[i].x)*(up-down)); //取子矩形的面积
if(a[j].y<=a[i].y) down=max(a[j].y,down);
if(a[j].y>=a[i].y) up=min(a[j].y,up); //更新up和down
}
ans=max(ans,(l-a[i].x)*(up-down));
}
for(int i=n;i>=1;i--) { //操作同上
int down=0,up=w;
for(int j=i-1;j>1;j--) {
ans=max(ans,(a[i].x-a[j].x)*(up-down));
if(a[j].y<=a[i].y) down=max(a[j].y,down);
if(a[j].y>=a[i].y) up=min(a[j].y,up);
}
ans=max(ans,a[i].x*(up-down));
}
sort(a+1,a+n+1,cmp2);
for(int i=1;i<n;i++) //求第二种情况
ans=max(ans,(a[i+1].y-a[i].y)*l);
printf("%d\n",ans);
return 0;
}
算法总结
- 枚举法的时间复杂度是 \(O(S^2)\) 。
虽然算法运用的极大化思想看起来是比较高效的,但也有使用的局限性。可以发现,这个算法的复杂度只与障碍点的个数 \(s\) 有关,但对于某些问题,\(s\) 最大有可能达到 \(n \times m\) ,当 \(s\) 较大时,这个算法就未必能满足时间上的要求了。
-
但我们可以发现,通过枚举所有的悬线,就可以枚举出所有的极大子矩形。由于每个悬线都与它底部的那个点一一对应,所以悬线的个数为 \((n-1) \times m\)(以矩形中除了顶部的点以外的每个点为底部,都可以得到一个悬线,且没有遗漏)。所以整个悬线法的时间复杂度为 \(O(NM)\) ,空间复杂度是 \(O(NM)\) 。
-
两个算法的对比:
以上说了两种具有一定通用性的处理算法,时间复杂度分别为 \(O(S^2)\) 和 \(O(NM)\) 。
两种算法分别适用于不同的情况:
从时间复杂度上来看,枚举算法+极大化思想对于障碍点稀疏的情况比较有效,悬线大法则与障碍点个数的多少没有直接的关系(当然,障碍点较少时可以通过对障碍点坐标的离散化来减小处理矩形的面积,不过这样比较麻烦,不如极大化思想的算法好),适用于障碍点密集的情况。
-
在处理障碍点不能作为边界的题时,尽量使用悬线法;
-
对于在矩形的边界上能包含障碍点的一类问题,极大化思想更加有效。
训练题
下面几道求最大子矩形的经典例题...
此处就不提供题解和思路了,请读者自行理解代码...
I. 最大正方形
来源于 洛谷 P1387 最大正方形
题目描述
在一个 \(n\times m\) 的只包含 \(0\) 和 \(1\) 的矩阵里找出一个不包含 \(0\) 的最大正方形,输出边长。
输入格式
输入文件第一行为两个整数 \(n,m(1\leq n,m\leq 100)\),接下来 \(n\) 行,每行 \(m\) 个数字,用空格隔开,\(0\) 或 \(1\)。
输出格式
一个整数,最大正方形的边长。
样例 #1
样例输入 #1
4 4
0 1 1 1
1 1 1 0
0 1 1 0
1 1 0 1
样例输出 #1
2
Code I
#include<bits/stdc++.h>
using namespace std;
const int N=101;
int n,m,a[N][N],ans;
int l[N][N],r[N][N],up[N][N];
bool vis[N][N];
int main() {
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) {
for(int j=1;j<=m;j++) {
l[i][j]=r[i][j]=j;
up[i][j]=1;
}
}
for(int i=1;i<=n;i++) {
for(int j=1;j<=m;j++) {
scanf("%d",&a[i][j]);
if(a[i][j]==0)
vis[i][j]=1;
}
}
for(int i=1;i<=n;i++) {
for(int j=2;j<=m;j++) {
if(!vis[i][j]&&!vis[i][j-1])
l[i][j]=l[i][j-1];
}
}
for(int i=1;i<=n;i++) {
for(int j=m-1;j>=1;j--) {
if(!vis[i][j]&&!vis[i][j+1])
r[i][j]=r[i][j+1];
}
}
for(int i=1;i<=n;i++) {
for(int j=1;j<=m;j++) {
if(i>1&&!vis[i][j]&&!vis[i-1][j]) {
l[i][j]=max(l[i][j],l[i-1][j]);
r[i][j]=min(r[i][j],r[i-1][j]);
up[i][j]=up[i-1][j]+1;
}
ans=max(ans,min(r[i][j]-l[i][j]+1,up[i][j]));
}
}
printf("%d\n",ans);
return 0;
}
II. 玉蟾宫
来源于洛谷 P4147 玉蟾宫
题目背景
有一天,小猫 rainbow 和 freda 来到了湘西张家界的天门山玉蟾宫,玉蟾宫宫主蓝兔盛情地款待了它们,并赐予它们一片土地。
题目描述
这片土地被分成 \(N\times M\) 个格子,每个格子里写着 'R' 或者 'F',R 代表这块土地被赐予了 rainbow,F 代表这块土地被赐予了 freda。
现在 freda 要在这里卖萌。。。它要找一块矩形土地,要求这片土地都标着 'F' 并且面积最大。
但是 rainbow 和 freda 的 OI 水平都弱爆了,找不出这块土地,而蓝兔也想看 freda 卖萌(她显然是不会编程的……),所以它们决定,如果你找到的土地面积为 \(S\),它们每人给你 \(S\) 两银子。
输入格式
第一行两个整数 \(N\),\(M\),表示矩形土地有 \(N\) 行 \(M\) 列。
接下来 \(N\) 行,每行 \(M\) 个用空格隔开的字符 'F' 或 'R',描述了矩形土地。
输出格式
输出一个整数,表示你能得到多少银子,即 (\(3\times \text{最大 'F' 矩形土地面积}\)) 的值。
样例 #1
样例输入 #1
5 6
R F F F F F
F F F F F F
R R R F F F
F F F F F F
F F F F F F
样例输出 #1
45
提示
对于 \(50\%\) 的数据,\(1 \leq N, M \leq 200\)。
对于 \(100\%\) 的数据,\(1 \leq N, M \leq 1000\)。
Code II
#include<bits/stdc++.h>
using namespace std;
const int N=1001;
char a[N][N];
int n,m,ans,sum;
int l[N][N],r[N][N],up[N][N];
bool vis[N][N];
int main() {
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) {
for(int j=1;j<=m;j++) {
l[i][j]=r[i][j]=j;
up[i][j]=1;
}
}
for(int i=1;i<=n;i++) {
for(int j=1;j<=m;j++) {
cin>>a[i][j];
if(a[i][j]=='R')
vis[i][j]=1;
else sum++;
}
}
if(sum==0) {
printf("0\n");
return 0;
}
for(int i=1;i<=n;i++) {
for(int j=2;j<=m;j++) {
if(!vis[i][j]&&!vis[i][j-1])
l[i][j]=l[i][j-1];
}
}
for(int i=1;i<=n;i++) {
for(int j=m-1;j>=1;j--) {
if(!vis[i][j]&&!vis[i][j+1])
r[i][j]=r[i][j+1];
}
}
for(int i=1;i<=n;i++) {
for(int j=1;j<=m;j++) {
if(i>1&&!vis[i][j]&&!vis[i-1][j]) {
l[i][j]=max(l[i][j],l[i-1][j]);
r[i][j]=min(r[i][j],r[i-1][j]);
up[i][j]=up[i-1][j]+1;
}
ans=max(ans,(r[i][j]-l[i][j]+1)*up[i][j]);
}
}
printf("%d\n",ans*3);
return 0;
}
III. [ZJOI2007] 棋盘制作
题目描述
国际象棋是世界上最古老的博弈游戏之一,和中国的围棋、象棋以及日本的将棋同享盛名。据说国际象棋起源于易经的思想,棋盘是一个\(8 \times 8\)大小的黑白相间的方阵,对应八八六十四卦,黑白对应阴阳。
而我们的主人公小Q,正是国际象棋的狂热爱好者。作为一个顶尖高手,他已不满足于普通的棋盘与规则,于是他跟他的好朋友小W决定将棋盘扩大以适应他们的新规则。
小Q找到了一张由\(N \times M\)个正方形的格子组成的矩形纸片,每个格子被涂有黑白两种颜色之一。小Q想在这种纸中裁减一部分作为新棋盘,当然,他希望这个棋盘尽可能的大。
不过小Q还没有决定是找一个正方形的棋盘还是一个矩形的棋盘(当然,不管哪种,棋盘必须都黑白相间,即相邻的格子不同色),所以他希望可以找到最大的正方形棋盘面积和最大的矩形棋盘面积,从而决定哪个更好一些。
于是小Q找到了即将参加全国信息学竞赛的你,你能帮助他么?
输入格式
包含两个整数\(N\)和\(M\),分别表示矩形纸片的长和宽。接下来的\(N\)行包含一个\(N \ \times M\)的\(01\)矩阵,表示这张矩形纸片的颜色(\(0\)表示白色,\(1\)表示黑色)。
输出格式
包含两行,每行包含一个整数。第一行为可以找到的最大正方形棋盘的面积,第二行为可以找到的最大矩形棋盘的面积(注意正方形和矩形是可以相交或者包含的)。
样例 #1
样例输入 #1
3 3
1 0 1
0 1 0
1 0 0
样例输出 #1
4
6
提示
对于\(20\%\)的数据,\(N, M ≤ 80\)
对于\(40\%\)的数据,\(N, M ≤ 400\)
对于\(100\%\)的数据,\(N, M ≤ 2000\)
Code III
#include<bits/stdc++.h>
using namespace std;
const int N=2001;
int n,m,a[N][N],ans,ans2;
int l[N][N],r[N][N],up[N][N];
int main() {
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) {
for(int j=1;j<=m;j++) {
cin>>a[i][j];
l[i][j]=r[i][j]=j;
up[i][j]=1;
}
}
for(int i=1;i<=n;i++) {
for(int j=2;j<=m;j++) {
if(a[i][j]!=a[i][j-1])
l[i][j]=l[i][j-1];
}
}
for(int i=1;i<=n;i++) {
for(int j=m-1;j>=1;j--) {
if(a[i][j]!=a[i][j+1])
r[i][j]=r[i][j+1];
}
}
for(int i=1;i<=n;i++) {
for(int j=1;j<=m;j++) {
if(i>1&&a[i][j]!=a[i-1][j]) {
l[i][j]=max(l[i][j],l[i-1][j]);
r[i][j]=min(r[i][j],r[i-1][j]);
up[i][j]=up[i-1][j]+1;
}
int s=r[i][j]-l[i][j]+1;
int t=min(s,up[i][j]);
ans=max(t*t,ans);
ans2=max(s*up[i][j],ans2);
}
}
printf("%d\n%d\n",ans,ans2);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号