2018.10.06【NOIP提高组】模拟B组

喝喝喝 (NOIP2015模拟)

Time Limits:2000 ms
Memory Limits:131072 KB

\(Description\)

\(Input\)

3 2
5 3 1

\(Output\)

4

\(Data\ Constraint\)

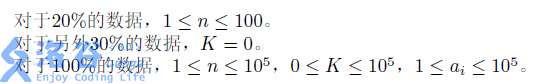
一道很神奇的题目。具体做法是两边缩减找“坏对”。

Uses math;

var
	maxn,tmp,l,r,i,j,n,k:longint;
	num,bucket:array[-1..100007] of longint;
	ans:int64;
begin
	assign(input,'drink.in'); reset(input);
	assign(output,'drink.out'); rewrite(output);
	read(n,k); for i:=1 to n do begin read(num[i]); maxn:=max(maxn,num[i]); end;
	l:=1; r:=1; ans:=n;
	inc(bucket[num[1]]);
	while r<=n do
        begin inc(r); if r>n then break;
		if num[r]>k then
			for i:=0 to maxn do
			begin
				tmp:=i*num[r]+k;
				if tmp>maxn then break;
				while (bucket[tmp]<>0) do begin dec(bucket[num[l]]); inc(l); end;
			end; 
               inc(bucket[num[r]]); inc(ans,r-l);
	end;
	writeln(ans);
	close(input); close(output);
end.

图 (NOIP2017提高A组)

Time Limits:2000 ms
Memory Limits:524288 KB

\(Description\)

有一个n个点n条边的有向图，每条边为\(<i,f(i),w(i)>\),意思是 \(i\) 指向 \(f(i)\) 的边权为 \(w(i)\) 的边，现在小A想知道，对于每个点的 \(si\) 和\(mi\)。

• \(si\):由 \(i\) 出发经过 \(k\) 条边，这 \(k\) 条边的权值和。
• \(mi\):由 \(i\) 出发经过 \(k\) 条边，这 \(k\) 条边的权值最小值。

\(Input\)

第一行两个数 \(n\) 和 \(k\)
第二行 \(n\) 个数 \(f(i)\)
第三行 \(n\) 个数 \(w(i)\)。

7 3
1 2 3 4 3 2 6
6 3 1 4 2 2 3

\(Output\)

每行两个数 \(si\) 和 \(mi\)。

10 1
8 1
7 1
10 2
8 2
7 1
9 3

\(Data\ Constraint\)

\(100\)% 的数据：\(N\leq10^5\) , \(k\leq10^10\) , \(0 \leq f(i) \leq n\) , \(w(i)\leq10^8\)。

直接上倍增,没有什么好说的。

Uses math;

var
    get,minn,sum:array[-1..100007,-1..36] of int64;
    log:array[-1..36] of int64;
    n,i,j:longint;
    k,logk,sumans,minans,x,fuck:int64;

begin
    read(n,k); logk:=0; log[0]:=1;
    for i:=1 to n do read(get[i-1,0]);
    for i:=1 to n do begin read(sum[i-1,0]); minn[i-1,0]:=sum[i-1,0]; end;
    for i:=1 to 35 do log[i]:=log[i-1]*2;
    for i:=1 to 35 do if log[i]>=k then begin logk:=i; break; end;
    for j:=1 to logk+1 do
        for i:=0 to n-1 do
        begin
            get[i,j]:=get[get[i,j-1],j-1];
            minn[i,j]:=min(minn[get[i,j-1],j-1],minn[i,j-1]);
            sum[i,j]:=sum[get[i,j-1],j-1]+sum[i,j-1];
        end;

    for i:=0 to n-1 do
    begin
        x:=i; sumans:=0; minans:=maxlongint div 843; fuck:=k;
        for j:=logk+1 downto 0 do
            if fuck>=log[j] then
            begin
                dec(fuck,log[j]);
                inc(sumans,sum[x,j]);
                minans:=min(minans,minn[x,j]);
                x:=get[x,j];
            end;
        writeln(sumans,' ',minans);
    end;
end.

表达式 (NOIP2017提高A组模拟)

Time Limits:1000 ms
Memory Limits:524288 KB

\(Description\)

求 \(\sum\limits^{k*p}_{i=1}i^{2p-1} \mod p^2\) 的值。

\(Input\)

给出 \(k,p\) 。

1 3

\(Output\)

只有一行表示答案。

6

\(Data\ Constraint\)

对于 \(100\)%的数据：\(k,p\leq10^9\) 。

有人是用找规律的,这题要化简。直接写最终的答案:

\(\frac{(k+p)*k*p}{2}\mod p^2\)

\(10^{10}\) 会炸掉,还要委婉的相乘。这里就不必了。

var k,p:int64;
begin
	read(k,p); writeln(((k+p)*((k*p) mod (p*p)) div 2) mod (p*p));
end.