P4168 [Violet]蒲公英
好久以前就要写的博客拖到运动会来写....(当时思路好像还是原创的,现在不是了)
先说明并没有 \(A\) 这道题,但是 \(A\) 了 \(loj\) 分块 \(9\) (也是区间众数,我是按在线做的)。如果有大佬知道为什么我没有 \(A\) 蒲公英可以来 @ 我!。
本篇适合于刚刚入手分块的蒟蒻(超详细)。
首先我们先把区间分块(废话)。考虑到一个区间的众数是要不是这个区间的最大块的答案,就是旁边多出来的边角的数字。因为任何数在最大块中出现的次数 肯定小于 最大块的众数的出现次数,而边角却可以让自己的出现次数增加来达到超越最大块的众数的效果。
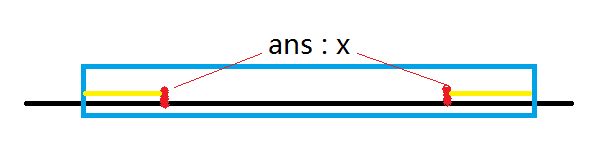
(如图,黄色部分的数字的出现次数可能超过最大块众数 \(x\) 的出现次数,红色为最大块的边界)
所以我们就可以预处理出第 \(i\) 块到第 \(j\) 块的众数,且要知道最大块中的每个数字的出现次数。
首先要预处理每个块中数的出现次数。如果我们定义数组 \(times[i,j,x]\) 代表 \(i\) 块到 \(j\) 块的出现次数的话,空间爆炸 \(n \times \sqrt{n} \times \sqrt{n}\) --- \(O(n^2)\)。如果我们用 \(times[i,x]\) 表示第 \(i\) 块 \(x\) 的出现次数的话,时间复杂度爆炸 --- 一次查询 \(O(\sqrt{n} \times \sqrt{n})\) (因为我们还要一块一块的找出现次数,本来的时间复杂度就 \(\sqrt{n}\))。然后我们就机制的把 \(times[i,x]\) 定义为 \(1\)~\(i\) 的 \(x\) 的出现次数。那我们查询第 \(i\) 块到第 \(j\) 块的出现次数就是 \(times[i,x]-times[j-1,x]\) 了。预处理复杂度 \(O(n \sqrt{n})\)。(离散化以后)
j:=1;
for i:=1 to n do
begin
inc(times[j,num[i]]);
if i mod (block_num-1)=0 then // block_num 代表块的个数
begin
for k:=1 to tail do times[j+1,k]:=times[j,k]; // 全部数字都要继承
inc(j); // 又过了一块
end;
end;
接下来我们要快速构造数组 \(ans[i,j]\) 代表第 \(i\) 块到第 \(j\) 块的答案。我们想,如果我们已经有了 \(ans[i,j-1]\),我们如何求 \(ans[i,j]\) ? 暴力跑一遍啊!反正中间只有 \(\sqrt{n}\) 个数字! 为什么上一个答案可以拿来比较? 因为 \(i,j\) 包括着 \(i,j-1\),我们已知的众数只有 \(ans[i-1,j]\),那么只有块 \(j-1\) 到块 \(j\) 这个地方又可能超过原有的众数,其实就是一个查询。 其中我们要两个循环 \(i,j\) 所以时间复杂度变为 \(\sqrt{n} \times \sqrt{n}\) --- \(O(n)\),然后暴力扫,变为 \(O(n \sqrt{n})\)。
for i:=1 to block_num do
for j:=i to block_num do
begin
now:=ans[i,j-1]; // 上一次的答案
for k:=(j-1)*node_num+1 to min(n,j*node_num) do // 这个块
begin
tmp1:=times[j,num[k]]-times[i-1,num[k]]; // 现有答案的出现次数
tmp2:=times[j,now]-times[i-1,now]; // 可能的数的出现次数
if (tmp1>tmp2)or((tmp1=tmp2)and(num[k]<now)) then now:=num[k]; // 更好就更新
end;
ans[i,j]:=now;
end;
查询的思路讲得很清楚了,大家主要看注释。
讲一下定义:
- \(Ready\) 输入 \(+\) 离散化 \(+\) 预处理
- \(now\) 答案的离散化后的编号
- \(recf\) 编号所对应的原有数组
- \(Locate\) 这个位置在第几块
- \(real[1\)~\(2]\) 最大块的边界的块编号 (比如 \(l=1\) 的时候 \(real[1]=1\),\(r=n\) 的时候 \(real[2]=Locate(n)\))
- \(bucket\) 这个数字在边角的出现次数
- \(node_{num}\) 每个块的数字个数
begin
Ready; now:=0; recf[0]:=0; // 一开始 now=0
for i:=1 to m do
begin
read(l,r);
real[1]:=Locate(l); real[2]:=Locate(r); bucket[0]:=0;
if real[2]-real[1]<=1 then // 可以暴力就暴力 复杂度是两个 sqrt(n)
begin
now:=0;
for k:=l to r do
begin
inc(bucket[num[k]]);
if (bucket[num[k]]>bucket[now])or((bucket[num[k]]=bucket[now])and(now>num[k])) then now:=num[k];
end;
for k:=l to r do bucket[num[k]]:=0;
writeln(recf[now]);
end
else
begin // 只有左右需要暴力,还要清空,所以是四个 sqrt(n)
now:=ans[real[1]+1,real[2]-1]; // 最大块的出现次数
for k:=l to min(n,real[1]*node_num) do // 左边角暴力
begin
inc(bucket[num[k]]);
tmp1:=bucket[num[k]]+times[real[2]-1,num[k]]-times[real[1],num[k]];
tmp2:=bucket[now]+times[real[2]-1,now]-times[real[1],now];
if (tmp1>tmp2)or((tmp1=tmp2)and(now>num[k])) then now:=num[k];
end;
for k:=(real[2]-1)*node_num+1 to r do // 右边角暴力
begin
inc(bucket[num[k]]);
tmp1:=bucket[num[k]]+times[real[2]-1,num[k]]-times[real[1],num[k]];
tmp2:=bucket[now]+times[real[2]-1,now]-times[real[1],now];
if (tmp1>tmp2)or((tmp1=tmp2)and(now>num[k])) then now:=num[k];
end;
// 清空
for k:=l to min(n,real[1]*node_num) do bucket[num[k]]:=0;
for k:=(real[2]-1)*node_num+1 to r do bucket[num[k]]:=0;
writeln(recf[now]);
end;
end;
end.
写了好久,希望给个赞再走 \(QwQ\)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号