万恶的三校联考

提高组

\[\text{ST数} \]

求:

\[\sum\limits^{R}_{i=L}ST(i) \]

\(ST(i)=i\) 的约数个数。

\(L \leq R \leq 10^7\)

并不知道怎么推公式,所以就暴力直接跑。

时间复杂度:

\[\sum\limits^{T}_{i=1}\frac{T}{i} \]

怎么办,大概是 \(1.6 \times 10^8\)。况且我还用了 \(Pascal\)。

后面想到一种卡常方法,只要不开数组就可以了。\(1400+ms\ ->\ 800ms\)。

预计得分: \(100pts\)。

实际得分: \(100pts\)。

// T1

var
	i,j,s,t:longint;
	ans:int64;
begin
	read(s,t);
	for i:=2 to t do
	begin
	    j:=i; while j<=t do begin if (j>=s) then inc(ans); inc(j,i); end;
	end;
   writeln(ans+t-s+1);
end.

\[\text{彩带} \]

给你一个序列,每一个位置有多种颜色,要求求一个最小的完整的序列且包含所有颜色。序列很长, \(2^{31}\)。

考虑到这种东西可以用队列来求,然后我就离散化一下就好了。

预计得分: \(100pts\)。

实际得分: \(0pts\)。(原因竟然是没有输出)

// T2

Uses math;

var
	num,node:array[-1..2100000] of int64;
	bucket:array[-1..10000] of longint;
	n,m,k,p,tail,he,ta,kind,ans:int64;
	i,j:longint;

procedure Swap(var x,y:int64);var t:longint; begin t:=x; x:=y; y:=t; end;

procedure Sort(l,r:longint);
var i,j,s:longint;
begin
   i:=l; j:=r; s:=num[(l+r) >> 1];
    repeat
        while num[i]<s do inc(i);
        while num[j]>s do dec(j);
        if i<=j then 
        begin
        	Swap(num[i],num[j]);
        	Swap(node[i],node[j]); 
        	inc(i); dec(j); 
       	end;
    until i>=j;
    if i<r then Sort(i,r);
    if j>l then Sort(l,j);
end;

begin
	read(n,m); tail:=0; ans:=maxlongint*888; num[0]:=-1;
	for i:=1 to m do
	begin
		read(k);
		for j:=1 to k do  begin read(p); inc(tail); num[tail]:=p; node[tail]:=i; end;
	end;
	Sort(1,tail); kind:=0; he:=0;
	for i:=1 to tail do
	begin
		if bucket[node[i]]=0 then inc(kind); inc(bucket[node[i]]);
		while kind>=m do
		begin
			inc(he); dec(bucket[node[he]]);
			if bucket[node[he]]=0 then dec(kind);
            ans:=min(ans,num[i]-num[he]);
		end;
	end;
        writeln(ans);
end.

\[\text{矩阵土地} \]

给你一个矩阵(\(N \times N\)),有一些障碍和空地,让你求移走 \(K\) 个障碍以后两个空地之间的最长距离。\(N \leq 3\times 10\)。

只需要求出一个坐标点 \(x,y\) 到另一个坐标点 \(l,r\) 经过的障碍个数就可以了。偷懒用了 \(Floyd\)。

这是神马情况:

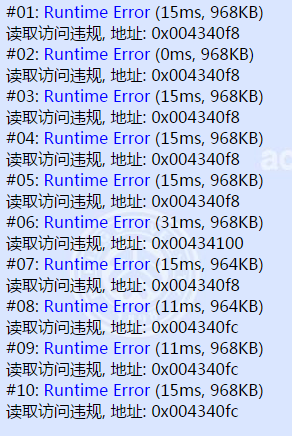
预计得分 : \(50\)~\(80pts\)。

实际得分 : \(0pts\)。

// T3

Uses math;

var
	id:array[-1..122,-1..122] of longint;
	table:array[-1..122,-1..122] of longint;
	i,j,n,m,k,l,r,num,tmp,node:longint;
	s:string;
	ans:real;

function Judge(x,y:longint):boolean;
begin
	if (x=0)or(y=0)or(x=n+1)or(y=m+1) then exit(False); exit(True);
end;

function Disq(l,r,x,y:longint):real;
begin
	l:=(l-x)*(l-x); r:=(r-y)*(r-y); exit(sqrt(l+r));
end;

procedure link(x,y,sum:longint);
begin
	table[x,y]:=max(table[x,y],sum); table[y,x]:=max(table[x,y],max(table[y,x],sum));
end;

begin
    for i:=1 to 31 do for j:=1 to 31 do table[i,j]:=-maxlongint div 8333;
	readln(n,m,tmp); node:=n*m; num:=0; ans:=-maxlongint div 8333;
	for i:=1 to n do for j:=1 to m do begin inc(num); id[i,j]:=num; end;
	for i:=1 to n do
	begin
		readln(s);
		for j:=1 to m do
		begin
			val(s[j],k);
            if k=1 then
            begin
                for k:=1 to node do link(k,id[i,j],1); continue;
            end;
			if Judge(i-1,j) then link(id[i-1,j],id[i,j],0);
			if Judge(i+1,j) then link(id[i+1,j],id[i,j],0);
			if Judge(i,j-1) then link(id[i,j-1],id[i,j],0);
			if Judge(i,j+1) then link(id[i,j+1],id[i,j],0);
		end;
	end;
	for k:=1 to node do
		for i:=1 to node do
			for j:=1 to node do
            begin
				table[i,j]:=min(table[i,j],table[i,k]+table[k,j]);
            end;
	for i:=1 to n do
		for j:=1 to m do
			for l:=1 to n do
				for r:=1 to m do
				begin
					if table[id[i,j],id[l,r]]>tmp then continue;
					ans:=max(ans,Disq(i,j,l,r));
				end;
	writeln(ans:0:6);
end.

\[\text{紧急任务} \]

给你一个图,然后让你求有多少种方法可以从 \(1 -> N\) 号点且用时为 \(T\)。

不会,直接爆搜。

预计得分 : \(30pts\)。

实际得分 : \(30pts\)。

// T4

var
	table:array[-1..11,-1..11] of longint;
	i,j,n,m,ans:longint;
    s:string;

procedure Dfs(x,dis:longint);
var i:longint;
begin
	if dis>m then exit;
	if (dis=m)and(x=n) then begin inc(ans); exit; end;
	for i:=1 to n do if (table[x,i]<>0) then Dfs(i,dis+table[x,i]);
end;

begin
	readln(n,m);
	for i:=1 to n do
    begin
        readln(s);
        for j:=1 to n do val(s[j],table[i,j]);
    end;
	Dfs(1,0);
    writeln(ans mod 2009);
end.

总结:

杀马特