第三次作业 崂山x牛x大队被卷积神经网络拿捏
一组第三次小组作业,卷积神经网络
【第一部分】视频学习心得及问题总结
吴博群
总结部分
- Cross Entropy Loss Function(交叉熵损失函数)可以用于二分类和多分类
在二分类的情况下,模型最后需要预测的结果只有两种情况,对于每个类别我们的预测得到的概率为 和
,此时表达式为:
其中:
- —— 表示样本
的label,正类为1 ,负类为 0
- —— 表示样本
预测为正类的概率
多分类的情况实际上就是对二分类的扩展:
其中:
- ——类别的数量
- ——符号函数(
或
),如果样本
的真实类别等于
取
,否则取
- ——观测样本
属于类别
的预测概率
由公式可知,受的控制,一次只会有一个log生效,即只有一个
不为0,此时取值决定于后面的log,如果其预测了一个很大的概率,即log部分会接近于0,如果预测了一个很小的错误,则是一个绝对值很大的负数。(一般先通过softmax计算概率后,再使用交叉熵损失函数)
因此我们可知,当预测分布越接近真实分布,交叉熵损失越小,预测分布越远离真实分布,交叉熵损失越大
- 全连接神经网络参数计算:输入长度*该层神经元个数+偏置(该层神经元个数)= 该层参数。
- 卷积神经网络:局部关联,参数共享
- 卷积神经网络中池化层可以缓解卷积层对位置的敏感性
- 计算图像经过卷积核卷积后的特征图大小

- 卷积核(共享权重),再加上同一个偏置(共享偏置)。如果没有用共享权值,那么一个神经元需要对应一个卷积核一个偏置,而现在是每个神经元对应的是同一个卷积核同一个偏置,显然参数量大幅下降
- 不管输入图像的深度为多少(算术求和),经过一个卷积核(filter),变成一个深度为1的特征图。
- DropOut相当于隐式的模型集成
- 卷积核 参数量=(filter size * 前一层特征图的通道数 )* 当前层filter数量 + 偏置
- 残差神经网络可以用来防止梯度消失,训练非常深的网络结构,i并且可以自适应去学习应有的网络深度
疑问部分
- 是否需要在使用交叉熵之前,将数据映射到(0-1)的区间范围内部
- 卷积核一定需要偏置项嘛,什么情况下可以不使用,使用偏置项可以达到什么样的作用
- 批量归一化一般用在神经网络的哪个地方,以及和残差神经网络是什么样的关系
- F.nll_loss损失函数的实现细节,与一般的交叉熵损失函数区别
潘飞宇
绪论
卷积神经网络主要应用在图像、视觉等领域。
之前提到的传统神经网络,处理图像需要学习相当多的参数,容易导致过拟合。
卷积神经网络使用局部关联(卷积核,滤波器,filter来提取特征),参数共享(滑动窗口)等。降低了相当多的参数量。
卷积神经网络一般包括,卷积层,激活层,池化层,全连接层。
基本组成结构
卷积:
卷积是对两个实变函数(实数为自变量)的数学操作。
卷积核具有自己的参数。初始化后,在训练过程中反向传播更新参数。
特征图是输入经过卷积之后输出的结果。
深度是特征图的厚度,一个filter产生一层特征图,因而特征图深度与filter的个数保持一致。
池化:保留主要特征的同时,减少参数的计算量,防止过拟合,提高模型泛化能力。运算类似于卷积。
全连接:两层之间所有神经元都有权重连接。一般来说是参数量最大的层。其每一层是由许多神经元组成的的平铺结构。
卷积神经网络的典型结构
AlexNet:大数据 + ReLU + Dropout + Data augmentation
ZFNet:修改卷积层的感受野,步长和卷积核个数
VGG:更深层次的卷积神经网络
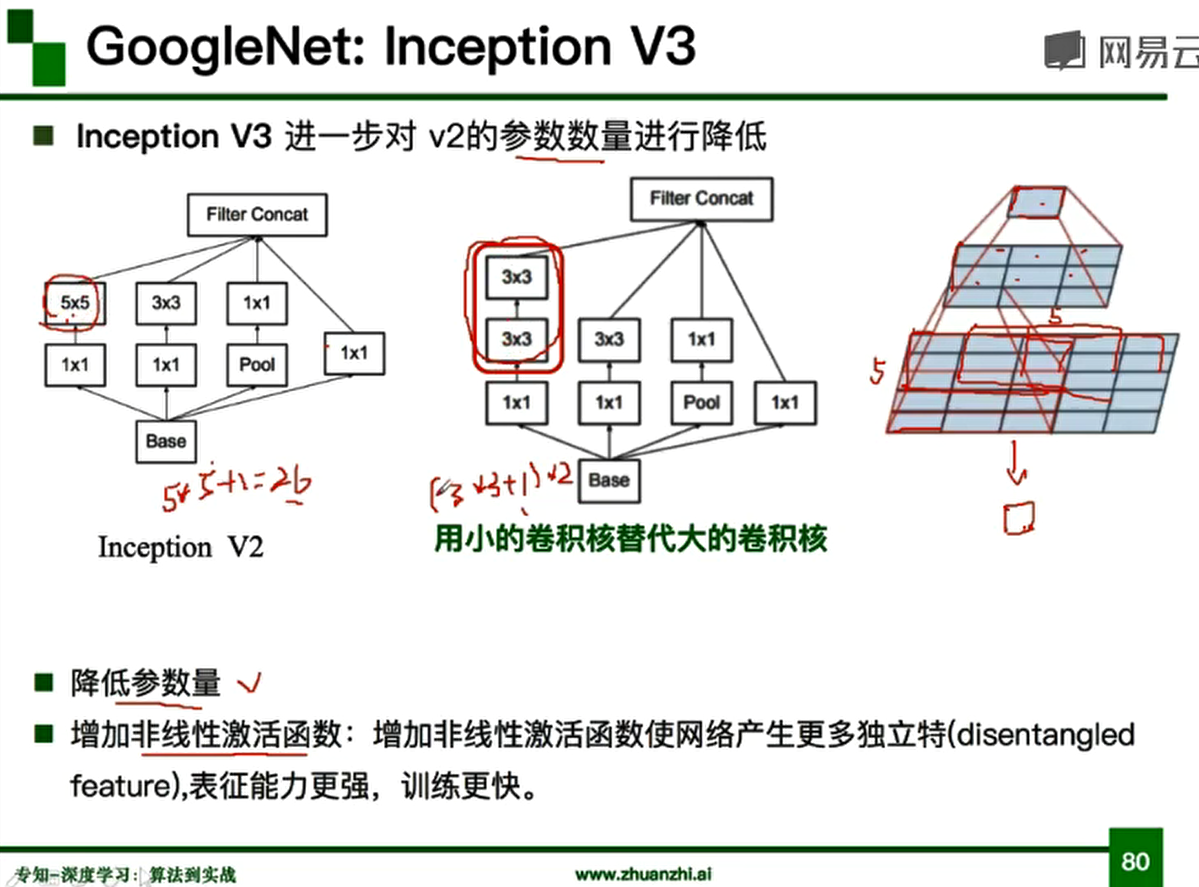
GoogleNet:采用了Inception模块,降低参数量
ResNet:利用残差,训练更深的网络
问题
- 更高维卷积的运算过程有些不太明白。
- 如何确定卷积的相关参数使效果更明显,以及卷积运算中设置偏置项bias的作用。
- 对一些卷积神经网络结构的理解还是有些模糊,例如不太清楚深度串联 和 ResNet中残差块的原理。
闫向前
视频学习心得:
学习心得:
此次视频学习主要介绍了卷积神经网络以及一些典型模型。
首先我们回顾了深度学习的三大步骤:
深度学习三部曲:
1、搭建神经网络
2、找到合适的损失函数:交叉熵损失、均方误差
3、找到合适的优化函数,更新参数:反向传播、随机梯度下降
之后我们了解了传统神经网络和卷积神经网络的不同,传统神经网络中,神经元与隐层输出以全连接的方式连接,参数过多,导致过拟合,过拟合的表现就是模型在训练集中的误差很小,但是在测试机中的误差却很大,导致过拟合的原因有训练集和测试集上的特征分布不一致、模型过于复杂(噪声数据也会被拟合)等。而卷积神经网络则是通过局部关联、参数共享来降低参数的数量。
卷积神经网络中主要有卷积层、池化层和全连接层。
卷积层的任务是通过卷积核/滤波器计算出特征图(y = wx + b w:卷积核/滤波器 x:卷积区域 b:偏置项),特征图的大小计算公式是:无padding:{(输入大小 - 卷积核大小)/步长 + 1},有padding:{(输入大小 + padding * 2 - 卷积核大小)/步长 + 1}
卷积核也可以称为权重矩阵,其值的大小就是该位置的权重。
池化就是在保留主要特征的同时减少参数量和计算量,也就是输入压缩,主要的两种池化方法是最大值池化和平均值池化。
虽然全连接不适合用于特征提取但是其可以将“分布式特征表示”映射到样本标记空间,起到“分类器”的作用。
之后我们了解了卷积神经网络的典型结构,如AlexNet,该模型使用了ReLU函数在一定程度上解决了传统Sigmoid函数梯度下降的问题、VGG,其使用了更多模型层数、GoogleNet模型以及ResNet。
ResNet中的残差思想:消除相同部分,突出微小差别。
问题:
什么情况下需要全连接层?尾部全连接层的作用是什么?
刘明晖
视频学习心得:
卷积神经网络可以处理图像以及一切可以转化成类似图像结构的数据。相比传统算法和其它神经网络,卷积神经网络能够高效处理图片的二维局部信息,提取图片特征,进行图像分类。通过海量带标签数据输入,用梯度下降和误差反向传播的方法训练模型。
问题:
卷积神经网络中的卷积核大小和卷积层数如何确定
李浩然
学习总结
传统神经网络,由于采用的是全连接的模式,所以在处理图片的问题是,由于参数太多,可能会存在过拟合的情况,卷积神经网络采用的是局部关联,参数共享,通过卷积核来提取图片的局部特征。如果当卷积核比较小,图像数据又很大的时候,卷积处理之后图像仍然很大,所以采用下采样,通过池化层来降低数据维度,能大大降低数据运算量。最后,经过卷积层和池化层的数据进入全连接层,用来输出想要的结果。实际操作中,卷积网络时常是这三种层堆叠而形成的。
对于几个经典的卷积神经网络模型,传统的神经网络普遍使用Sigmoid或者tanh等非线性函数作为激励函数,然而它们容易出现梯度弥散或梯度饱和的情况。在AlexNet中,使用了ReLU (Rectified Linear Units)激励函数替代Sigmoid/tanh,由于ReLU是线性的,且导数始终为1,计算量大大减少,收敛速度会比Sigmoid/tanh快很多。VGG相较于AlexNet而言,构建的是更深的神经网络,性能大幅提升。以当下视角来看,VGG并没有解决梯度过深导致反向传播消失这一现象,且当时GPU性能有限,所以深度网络不易于训练。再后来,为了训练更强大的神经网络,需要更深,更宽,但同时需要尽可能减少参数,所以GoogleNet提出了Inception方法,Inception就是把多个卷积或池化操作,放在一起组装成一个网络模块,设计神经网络时以模块为单位去组装整个网络结构。对于ResNet,是通过残差学习的方法,很好的解决了由于网络层数过深导致的网络退化问题。可以用来训练很深的神经网络。
刘玉龙
心得
了解到了什么是卷积、池化。卷积是通过不同的卷积核将图片的各个特征强化。在视频学习的前期对这个过程有些懵,不过随着后面给出了图片案例,我对卷积操作的目的和过程就清晰了不少。池化是在保留主要特征的同时减少参数和计算量,苍之过拟合以及提高模型泛化能力。但总体而言在学习过程中还是摸不到头脑。
问题
卷积核是怎么进行选择的?



 浙公网安备 33010602011771号
浙公网安备 33010602011771号