优化建图技巧
前言
优化建图指的是针对大规模边数,利用数据结构或其他技巧建出边数较少的等效图,或直接维护连通性,实现优化复杂度的目的。
有关题目的题单
线段树优化建图
CF786B Legacy
题意
有 \(n\) 个结点的图,有 \(m\) 次操作,每次操作有如下三种加边方法:
- $u \rightarrow v $,边权为 \(w\)
- \(u \rightarrow [l,r]\) 所有点,边权为 \(w\)。
- \([l,r]\) 所有点 \(\rightarrow u\),边权为 \(w\)。
求所有操作后点 \(s\) 到所有点的最短路。
solution
直接暴力建图边数是 \(n^2\) 的,考虑优化建图。
由于每次加边是对于一个区间加边,那么考虑用能高效解决区间问题的线段树来优化建图,具体地,我们可以构建如下模型:
例如,我们要让 \(8\) 号结点向 \([3,5]\) 内所有结点连边。
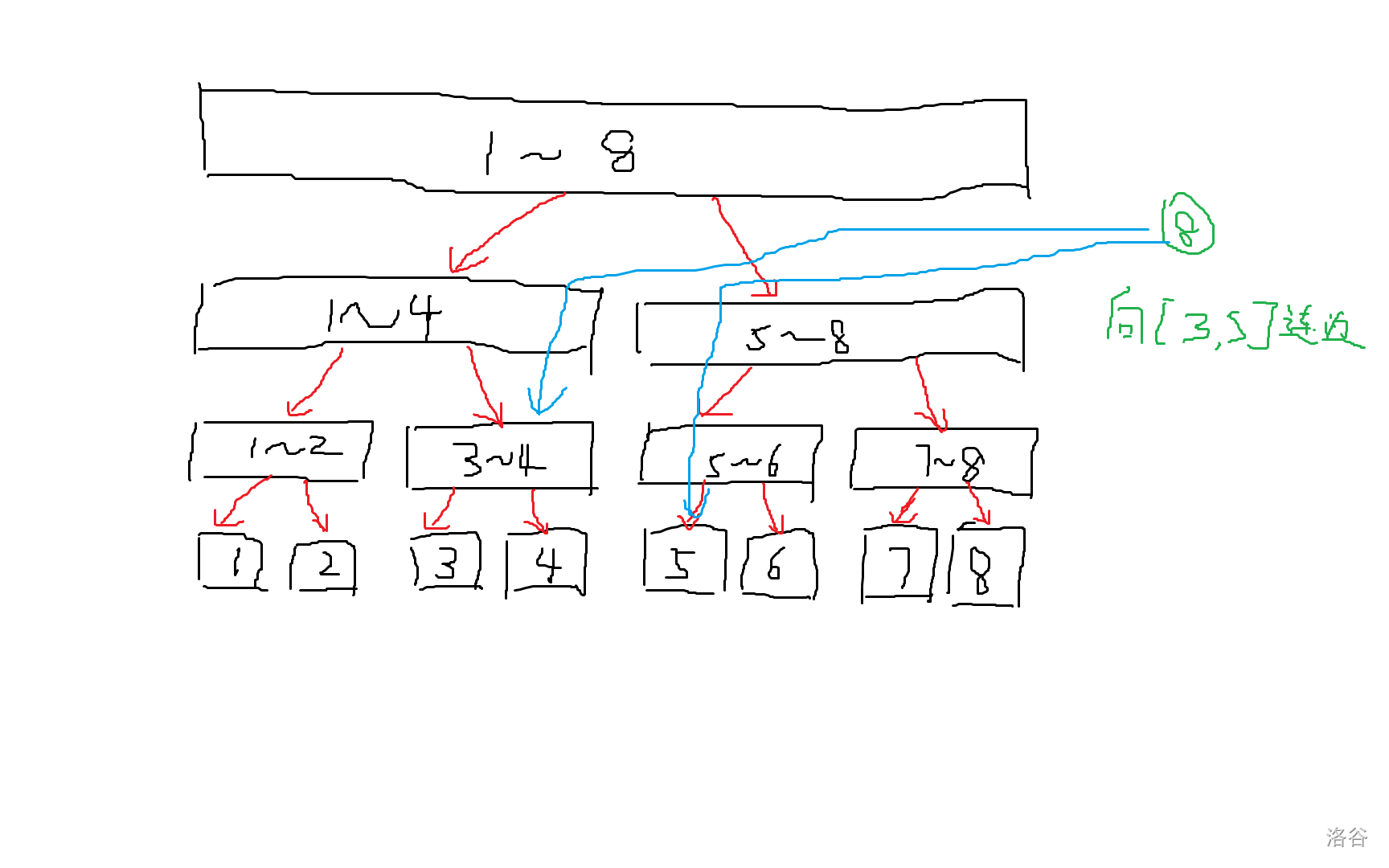
建一棵线段树,所有结点向它的左右儿子连一条边权为 \(0\) 的边(图中红色的边),类似于区间查询,令加边区间为 \([x,y]\),线段树当前节点管辖区间 \([l,r]\),若 \([x,y]\) 完全包含 \([l,r]\),那么直接对当前结点连边并退出,否则递归处理左右儿子,不难发现这样每次加边最多是 \(O(\operatorname{log}n)\) 条的,且完全等效于向区间每个点加边。
区间向点连边同理,我们只需要把线段树上的边反过来,即左右儿子父亲连边即可。
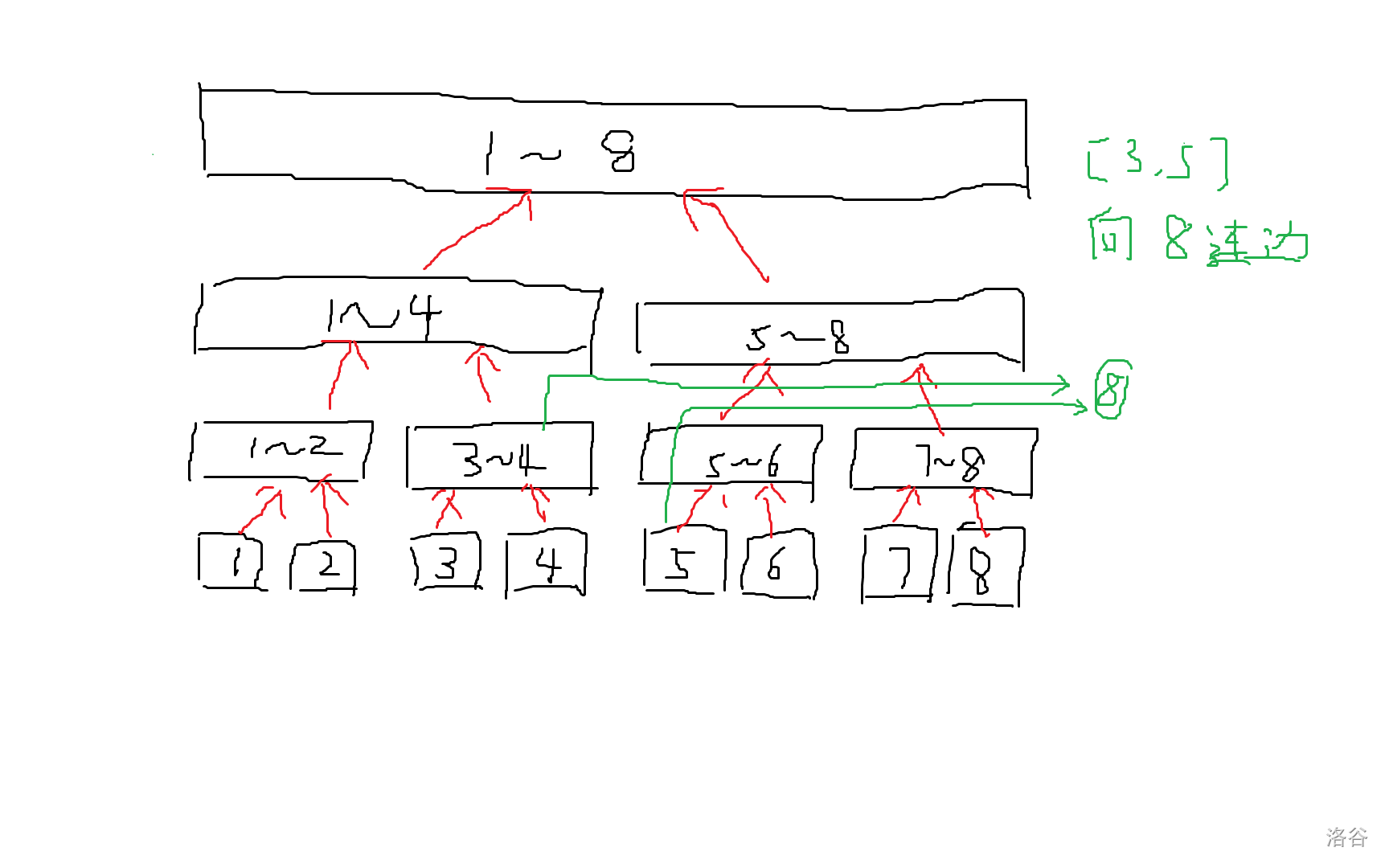
这样边数 \(O(m \operatorname{log}n)\),总复杂度 \(O(n \operatorname{log}^2n)\),满足题目要求。
P6348 [PA 2011] Journeys
题意
有 \(n\) 个点,\(m\) 次操作,每次操作给定 \(l_1,r_1,l_2,r_2\),对 \([l_1,r_1] \rightarrow [l_2,r_2]\) 连边,边权为 \(1\)。
求所有操作后点 \(s\) 到所有点的最短路。
\(n \le 5 \times 10^5\),\(m \le 10^5\)。
solution
与上题类似,我们可以建两棵线段树,每次操作建一个虚点,\([l_1,r_1]\) 所有点向这个虚点连边,虚点向 \([l_2,r_2]\) 连边即可。
由于边权为 \(0\) 和 \(1\),建出图后 01 bfs 可以做到 \(O(n\operatorname{log}n)\)。
其他的技巧
不止是最短路,线段树优化建图也可以解决差分约束等问题,具体实现就是在建图的基础上拓扑排序。
其他数据结构优化建图也很类似,比如倍增与树剖,就不多讲了。
习题
不建边优化空间
P5471 [NOI2019] 弹跳
题意
给定二位平面上的 \(n\) 个点,\(m\) 次操作,每次操作给定 \(p,l,r,u,d\) 表示 \(p\) 向满足 \(l\le x_v \le r \land u\le y_v \le d\) 的所有点 \(v\) 连边。
求所有操作后点 \(1\) 到所有点的最短路。
\(n \le 7\times 10^4\),\(m\le 1.5 \times 10^5\)。
solution
这个问题其实就是把一维上的加边转到二维了,所以把线段树换成 KDT(或者树套树)就解决了(吗?)。
实际上使用 KDT 边数是 \(O(m \sqrt n)\) 的直接 MLE 了,我们考虑如何解决这个问题。
借用题解区里的一句话:
- 首先你有一棵树
- 你要把这棵树完全变成你的工具
- 你建边的目的是要知道从一个点出发能到达哪些点
就是说,实际上我们根本不用建边,只要知道一个点能到达哪些点就行了(听起来有点神秘但确实是这样)。
建出一棵 KDT,直接跑 Dijkstra,把每次找下一个点的过程放到树上去做(也就是去树上找 \(dis_v > dis_u + w\) 且 \(u\) 可到达的点 \(v\)),然后正常松弛操作即可。
这个过程看似复杂度很高,实际上我们使用 KDT 的时候维护每个点的 \(dis\) 并动态更新,这样每个点松弛次数是可以保证的,因为有一些剪枝所以跑得甚至比直接建边还快,时间复杂度仍然为 \(O(n\sqrt n \operatorname{log} n)\),空间复杂度为 \(O(n)\)。这个思想非常重要,前面的线段树优化建图里有些题也需要应用这个技巧,有些题即使优化建图后边数仍然是不可接受的(或者建虚点会影响答案),关键在于跑对应的算法时(最短路,tarjan 等)复杂度均摊后时正确的,这时候就需要考虑对应的算法,建树出来动态修改才能做到优化复杂度。
P7712 [Ynoi2077] hlcpq
题意
给定 \(n\) 条水平线段和 \(n\) 条竖直线段,第 \(i\) 条水平线段纵坐标为 \(i\),第 \(i\) 条竖直线段横坐标为 \(i\),若两线段有交点则它们连通,将每条线段视为一个点,求哪些线段是割点。
\(n \le 10^5\)。
solution
这题就是上面所说的,直接建图是 \(O(n^2)\) 的,不能线段树直接建边的原因是建出线段树可能会影响原本图的连通性,无法保证正确性。
一条水平线段 \(i\) 对应 \([l_1,r_1]\) 与一条竖直线段 \(j\) 对应 \([l_2,r_2]\) 有交可以转化为 \(l_1 \le j \le r_1 \land l_2 \le i \le r_2\),不难发现这实际上就是扫描线板子,考虑每个点 \(i\) 维护一棵线段树表示满足 \(l_2 \le i \le r_2\) 的所有 \(j\),把 \(j\) 挂到线段树的第 \(j\) 个位置上,这个东西扫描线加可持久化线段树可以做到 \(O(n \operatorname{log} n)\),在此基础上,与 \(i\) 连通的点实际上就是在第 \(i\) 棵线段树上查询 \([l_i,r_i]\) 上的点 \(j\),那么我们就做到了维护连通性。
接下来我们直接对着 tarjan 求割点的板子进行魔改:
inline void tarjan(int now,int fl) {
dfn[now]=low[now]=++cnt;
int son=0;
for (int v:e[now]) {
if (!dfn[v]) {
son++;
tarjan(v,0);
low[now]=min(low[now],low[v]);
if (low[v]>=dfn[now]) ans[now]=1;
}
else low[now]=min(low[now],dfn[v]);
}
if (fl&&son>=2) ans[now]=1;
}
这是一份正常的求割点代码,因为我们没有建边,所以我们来考虑上面代码中 for 循环内的内容。
循环内的意思大致是这样:
- 对于没被遍历过的点,遍历它并令 \(low_u = \operatorname{min}(low_u,low_v)\)
- 对于已经遍历过的点,令 \(low_u = \operatorname{min}(low_u,low_v)\)
把所有连通的点分成以上两类。对于第一类直接暴力去做,从树上找一个没有被遍历过的点,拿出来遍历它,这样每个点最多遍历一次,拿出一个点的复杂度是 \(O(\operatorname{log}n)\) 级别的,那么总复杂度 \(O(n \operatorname{log} n)\)。对于第二类操作,相当于线段树上区间查询连通点 dfn 的最小值,每个点也是 \(O(\operatorname{log}n)\) 级别的,总复杂度 \(O(n \operatorname{log} n)\)。
魔改后代码:
inline void tarjan(int now,int fl) {
// p[x] 表示 线段x 对应 可持久化线段树上的编号
// tr[x].v 表示结点 x 的 dfn 最小值
// tr[x].c 表示未被遍历点数
if (fl) tr[p[now]].v=++tot,tr[p[now]].c=0;
dfn[now]=low[now]=tot;
int son=0;
// query函数用来求未被遍历点并更新 tr[x].v
for (int v;(v=query(L[now],R[now],1,m,rt[now]));son++) {
tarjan(v,0);
low[now]=min(low[now],low[v]);
vis[now]|=(low[v]>=dfn[now]);
}
// qmn函数用来求区间 dfn 最小值
low[now]=min(low[now],qmn(L[now],R[now],1,m,rt[now]));
if (fl) vis[now]=(son>=2);
}
这样我们就实现了不建边跑 tarjan,解决了此问题。
习题
其他优化技巧
其实可以用很多东西配合优化建图比如点分治,根号分治,2-sat 什么的,其实我不会,感兴趣的话可以自己学一学。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号