一些神秘的dp题
AT_agc076_a [AGC076A] Hamming-Distant Arrays
solution:
我们定义第 \(i\) 列的代价为这列出现最多的数的次数减 \(1\),令其为 \(s_i\)。
先给出结论:满足题意的构造方案的充要条件是 \(\sum_{i=1}^{n^2}s_i < n\)。
证明如下。
充分性:
若构造 \(y\) 使的每一行都为出现最多的数,那么总价值一定不会超过 \(n^2+\sum_{i=1}^{n^2}s_i\),即不超过 \(n \times (n+1)\),根据抽屉原理必然找得到一个满足条件的 \(x_i\)。
必要性:
反证,若价值之和大于等于 \(n\),找到 \(s_i\) 前 \(n\) 大的所有列,构造 \(y\) 使得这些列上的值为出现次数最多的值,那么对于会贡献大于等于 \(2n\) 个相似的位置(对于所有排列)。此时每一个排列于 \(y\) 所匹配的位置显然不会超过 \(n\),则不会导致代价的溢出(不会出现一列与 \(y\) 相匹配的位置数大于 \(n+1\)),那么只需要将按顺序对于 \(x_i\),将 \(y\) 中的空位放上与之匹配的数字直到其匹配位置数量正好为 \(n+1\) 即可。总价值最小为 \(2n + n \times (n-1) = n \times (n+1)\),由于不会造成价值溢出,所以构造出来的 \(y\) 一定能使所有 \(x_i\) 都不满足条件。
这个证明太神了!
知道了这个就好做了。令 \(f_{i,j,k}\) 表示将 \(j\) 种数填入 \(i\) 个空里其中出现最多的数的出现次数为 \(k\) 的方案数。那么显然有转移:
\(f_{i,j,k} \leftarrow f_{i-o,j-1,k} \times C(i,o)\) \((o < k)\)
\(f_{i,j,k} \leftarrow \sum_{l=0}^{k} f_{i-o,j-1,l} \times C(i,o)\) \((o=k)\)
做到 \(O(n^4)\) 处理出 \(f\) 数组,但是不知道能不能用多项式科技优化,这部分有个相似的题目 #5600. 最大值的期望(max)。
令 \(g_{i,j}\) 表示填了 \(i\) 列总代价为 \(j\) 的方案数。转移:
\(g_{i,j} \leftarrow \sum_{k=0}^{j}g_{i-1,j-k} \times f_{n,n,k+1}\)
答案即为 \(\sum_{j=0}^{n-1} g_{n \times n,j}\)。
总复杂度 \(O(n^4)\)。
Code
#include<cstdio>
#include<algorithm>
using namespace std;
#define ll long long
#define qwq Ff472130
#define f(i,l,r) for (int i=l;i<=r;i++)
#define F(i,l,r) for (int i=l;i>=r;i--)
const int N=50+10;
const int inf=1e9+10;
const int mod=998244353;
inline void add(int &x,int y){x+=((x+y>=mod)?(y-mod):y);}
inline void read(int &x) {
x=0;
char ch=getchar();
while (ch<48) ch=getchar();
while (ch>=48) x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
}
inline ll qpow(ll a,int b) {
ll res=1;
while (b) {
if (b&1) res=res*a%mod;
a=a*a%mod;
b>>=1;
}
return res;
}
int n,ans;
int f[N][N][N];
int g[N*N][N];
ll fac[N],inv[N];
inline void init(int n) {
fac[0]=inv[0]=1;
f(i,1,n) {
fac[i]=fac[i-1]*i%mod;
inv[i]=qpow(fac[i],mod-2);
}
}
inline int C(int n,int m) {
if (n<0||m<0||m>n) return 0;
return fac[n]*inv[m]%mod*inv[n-m]%mod;
}
int main() {
read(n);init(n);
f(i,0,n) f[0][i][0]=1;g[0][0]=1;
f(i,1,n) f(j,1,n) f(k,1,i) f(o,0,k) {
if (o!=k) add(f[i][j][k],1ll*f[i-o][j-1][k]*C(i,o)%mod);
else f(l,0,k) add(f[i][j][k],1ll*f[i-o][j-1][l]*C(i,o)%mod);
}
f(i,1,n*n) f(j,0,n) f(k,0,j) add(g[i][j],1ll*g[i-1][j-k]*f[n][n][k+1]%mod);
f(i,0,n-1) add(ans,g[n*n][i]);
printf("%d\n",ans);
return 0;
}
CF2003F Turtle and Three Sequences
solution:
神秘算法之 color-coding。
注意到 \(m\) 很小,所以先考虑 \(b_i \le m\) 的时候怎么做。显然可以令 \(dp_{i,j,k}\) 表示选到 \(i\) 已选数的集合为 \(j\) 且最后一个数为 \(k\) 时权值和最大值,可以得到转移:\(dp_{i,j,k} = \operatorname{max} (dp_{i-1,j,k},dp_{i-1,j \oplus b_{i},a_i}[b_i\notin j \land a_i > k])\),压掉一维并利用树状数组优化第三维即可做到 \(O(2^mn \operatorname{log} n)\)。
那么 \(b_i \ge m\) 时能不能映射到小于 \(m\) 的值域去做呢?考虑对于 \(b\) 的每个权值映射一小于 \(m\) 的颜色,使 \(b\) 相同一定对应相同的颜色,那么这样做得到的答案一定不会大于原答案(因为限制增多了)。这样做单次的正确率为 \(\frac{m!}{m^m}\),那么我们进行 \(T\) 次,正确率即为 \(1-(1-\frac{m!}{m^m})^T\),时间复杂度 \(O(T 2^m n \operatorname{log} n)\)。取 \(T=150\) 即可轻松通过。
Code
#include<cstdio>
#include<algorithm>
#include<random>
using namespace std;
#define ll long long
#define qwq Ff472130
#define f(i,l,r) for (int i=l;i<=r;i++)
#define F(i,l,r) for (int i=l;i>=r;i--)
const int N=3e3+10;
const int V=40;
const int S=(1<<5)-1;
const int inf=1e9+10;
inline void read(int &x) {
x=0;
char ch=getchar();
while (ch<48) ch=getchar();
while (ch>=48) x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
}
int n,m,ans=-1;
int a[N],b[N],c[N],mp[N];
mt19937 Ff(472130);
int dp[V];
struct BIT {
int v[N];
inline void clear() {f(i,1,n)v[i]=0;}
inline void add(int p,int k){for(;p<=n;p+=(p&-p))v[p]=max(v[p],k);}
inline int qry(int p){int res=0;for(;p;p-=(p&-p))res=max(res,v[p]);return res;}
}tr[V];
inline void solve() {
f(i,1,n) mp[i]=Ff()%5;
f(i,0,S) tr[i].clear();
f(i,1,n) {
const int d=(1<<mp[b[i]]);
dp[d]=c[i];
f(j,0,S) {
int res=tr[j].qry(a[i]);
if (!(j&d)&&res) dp[j|d]=max(dp[j|d],res+c[i]);
}
f(j,0,S) {
int cnt=0;
f(k,0,4) cnt+=((j>>k)&1);
if (cnt==m&&dp[j]) ans=max(ans,dp[j]);
if (dp[j]) tr[j].add(a[i],dp[j]);
dp[j]=0;
}
}
}
int main() {
read(n);read(m);
f(i,1,n) read(a[i]);
f(i,1,n) read(b[i]);
f(i,1,n) read(c[i]);
f(T,1,150) solve();
printf("%d\n",ans);
return 0;
}
P13795 [SWERC 2023] Flag performance
题意:
给定长度为 \(n\) 的排列 \(p\),你需要进行 \(k\) 次操作,每次操作可以交换其中两个元素,求进行 \(k\) 次操作后使排列满足 \(p_i = i\) 的方案数。
solution:
模拟赛死于不知道30的分拆数才5000多...
典中典 trick : 将 \(i\) 向 \(p_i\) 连边,形成若干个环,每次操作相当于合并两个环或者将一个环分裂为两个环,满足分裂或合并后环的大小之和不变,那么 \(p_i = i\) 可以看作形成了 \(n\) 个自环。
显然只与环的大小集合有关。
令 \(dp_{i,j}\) 为操作了 \(j\) 步形成环大小所构成集合为 \(i\) 的方案数。转移: \(dp_{i,j} \leftarrow dp_{nxt_i,j-1}\),其中 \(nxt_i\) 表示 \(i\) 进行一次操作所能形成的状态,由于可逆性显然从 \(nxt_i\) 进行一次操作变成状态 \(i\)。
\(i\) 的状态数实际上就是 \(n\) 的分拆数,只有 \(5604\) 个。预处理出所有 \(nxt_i\),实际上转移数有约 \(10^5\) 种。
时间复杂度 \(O(m^2+kS)\),其中 \(m\) 为 \(n\) 的分拆数, \(S \approx 10^5\)。
Code
#include<cstdio>
#include<algorithm>
#include<vector>
#include<unordered_map>
using namespace std;
#define ll long long
#define ull unsigned long long
#define qwq Ff472130
#define f(i,l,r) for (int i=l;i<=r;i++)
#define F(i,l,r) for (int i=l;i>=r;i--)
const int N=30+10;
const int V=6e3+10;
const int K=1e3+10;
const int inf=1e9+10;
const int mod=1e9+7;
inline void read(int &x) {
x=0;
char ch=getchar();
while (ch<48) ch=getchar();
while (ch>=48) x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
}
int n,m,cnt,flag;
int p[N],vis[N];
int dp[V][K],tmp[V][V];
vector<int> e[V];
vector<vector<int> > vec;
unordered_map<ull,int> mp;
const int Base=131;
inline ull H(vector<int> v) {
ull res=0;
for (int x:v) res=res*Base+x;
return res;
}
inline void dfs_init(vector<int> v,int mx,int sum) {
if (!sum) {
vec.push_back(v);
mp[H(v)]=++cnt;
return;
}
if (sum<mx) return;
f(i,mx,sum) {
vector<int> nxt=v;
nxt.push_back(i);
dfs_init(nxt,i,sum-i);
}
}
inline void get_nxt(vector<int> v) {
int now=0,Hv=mp[H(v)];
for (int x:v) p[++now]=x;
f(i,1,now) {
int k=p[i],mx=(k-1)/2;
vector<int> nxt;
f(j,1,now) if (i!=j) nxt.push_back(p[j]);
f(j,1,mx) {
vector<int> vnxt=nxt;
vnxt.push_back(j);
vnxt.push_back(k-j);
sort(vnxt.begin(),vnxt.end());
int Hnxt=mp[H(vnxt)];
if (!tmp[Hv][Hnxt]) e[Hv].push_back(Hnxt);
tmp[Hv][Hnxt]+=k;
}
if (!(k&1)) {
nxt.push_back(k/2);
nxt.push_back(k/2);
sort(nxt.begin(),nxt.end());
int Hnxt=mp[H(nxt)];
if (!tmp[Hv][Hnxt]) e[Hv].push_back(Hnxt);
tmp[Hv][Hnxt]+=k/2;
}
}
f(i,1,now) f(j,i+1,now) {
vector<int> nxt;
f(k,1,now) if (k!=i&&k!=j) nxt.push_back(p[k]);
nxt.push_back(p[i]+p[j]);
sort(nxt.begin(),nxt.end());
int Hnxt=mp[H(nxt)];
if (!tmp[Hv][Hnxt]) e[Hv].push_back(Hnxt);
tmp[Hv][Hnxt]+=p[i]*p[j];
}
if (now==n) flag=Hv;
}
inline void init() {
vector<int> cl;
dfs_init(cl,1,n);
for (vector<int> v:vec) get_nxt(v);
f(i,0,V-1) f(j,0,K-1) dp[i][j]=-1;
}
inline int get_v() {
f(i,1,n) vis[i]=0;
vector<int> v;
f(i,1,n) {
if (vis[i]) continue;
int now=i,siz=0;
while (!vis[now]) vis[now]=1,now=p[now],siz++;
v.push_back(siz);
}
sort(v.begin(),v.end());
return mp[H(v)];
}
inline int dfs(int now,int k) {
if (dp[now][k]!=-1) return dp[now][k];
if (!k) return dp[now][k]=(now==flag);
ll res=0;
for (int v:e[now]) res+=1ll*dfs(v,k-1)*tmp[now][v]%mod;
return dp[now][k]=res%mod;
}
inline void solve() {
f(i,1,n) read(p[i]);
printf("%d\n",dfs(get_v(),m));
}
int main() {
int T;
read(n);read(m);read(T);
init();
while (T--) solve();
return 0;
}
模拟赛题目
题意:
给定一个 \(n \times m\) 的网格图,网格有黑白两色,你可以将一些白色网格染成黑色,需要保证最后形成的图满足所有黑色格子形成一个凸连通块,求方案数。
solution:
经典对于凸连通块 dp,令 \(dp_{i,l,r,0/1,0/1}\) 表示已经填完了第 \(i\) 行,且这行染为黑色的左端点为 \(l\),右端点为 \(r\),左边是否存在 \(j \le i\) 满足 \(l_j>l_{j-1}\),右边是否存在 \(j \le i\) 满足 \(r_j<l_{r-1}\),即左边是否收缩,右边是否收缩。
简单推一下式子可以得到 \(O(n^5)\) 的暴力,利用前缀和优化可以做到 \(O(n^3)\),只不过实现可能有点恶心。
类似的题目:
Code
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
#define qwq Ff472130
#define ll long long
#define f(i,l,r) for (int i=l;i<=r;i++)
#define F(i,r,l) for (int i=r;i>=l;i++)
const int N=300+10;
const int inf=1e9+10;
const int mod=998244353;
inline void add(ll &x,ll y) {x+=((x+y>=mod)?(y-mod):y);}
inline void read(int &x) {
x=0;
char ch=getchar();
while (ch<48) ch=getchar();
while (ch>=48) x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
}
int n,m;
char mp[N][N];
int L[N],R[N],vis[N],fl[N];
ll dp[N][N][2][2],s[N][N][2][2],a[N][N][2][2];
ll ans;
inline void init() {
f(i,1,n) {
scanf("%s",mp[i]+1);
f(j,1,m) {
if (mp[i][j]!='#') continue;
if (!L[i]) L[i]=j;
R[i]=j;
}
}
f(i,1,n) {
if (L[i]) continue;
vis[i]=1;L[i]=m,R[i]=1;
}
int now=n,ok=1;
while (ok) {fl[now]=1;ok&=vis[now];now--;}
}
inline void get_sum() {
f(i,1,m) f(j,1,m) f(o1,0,1) f(o2,0,1) {
s[i][j][o1][o2]=(s[i-1][j][o1][o2]+s[i][j-1][o1][o2]-s[i-1][j-1][o1][o2]+a[i][j][o1][o2]+mod+mod+mod)%mod;
a[i][j][o1][o2]=0;
}
}
inline ll qsum(int l1,int r1,int l2,int r2,int o1,int o2,int l,int r) {
r1=min(r1,r);l2=max(l2,l);
return (s[r1][r2][o1][o2]-s[r1][l2-1][o1][o2]-s[l1-1][r2][o1][o2]+s[l1-1][l2-1][o1][o2]+mod+mod+mod+mod)%mod;
}
inline void solve() {
int lst=vis[1];
f(l,1,L[1]) f(r,max(l,R[1]),m) {
dp[l][r][1][1]=1;
a[l][r][1][1]=1;
if (fl[1]) add(ans,dp[l][r][1][1]);
}
f(i,2,n) {
get_sum();
memset(dp,0,sizeof(dp));
f(l,1,L[i]) f(r,max(l,R[i]),m) {
//ll<=r,rr>=l
//l=l'||r=r'
f(o1,0,1) f(o2,0,1) add(dp[l][r][o1][o2],qsum(l,l,r,r,o1,o2,l,r));
f(o,0,1) {
add(dp[l][r][0][o],qsum(1,l-1,r,r,0,o,l,r));
add(dp[l][r][0][o],qsum(1,l-1,r,r,1,o,l,r));
add(dp[l][r][o][0],qsum(l,l,r+1,m,o,0,l,r));
add(dp[l][r][o][0],qsum(l,l,r+1,m,o,1,l,r));
}
f(o,0,1) {
add(dp[l][r][1][o],qsum(l+1,m,r,r,1,o,l,r));
add(dp[l][r][o][1],qsum(l,l,1,r-1,o,1,l,r));
}
//1
add(dp[l][r][0][0],qsum(1,l-1,r+1,m,0,0,l,r));
add(dp[l][r][0][0],qsum(1,l-1,r+1,m,0,1,l,r));
add(dp[l][r][0][0],qsum(1,l-1,r+1,m,1,0,l,r));
add(dp[l][r][0][0],qsum(1,l-1,r+1,m,1,1,l,r));
//2
add(dp[l][r][0][1],qsum(1,l-1,1,r-1,0,1,l,r));
add(dp[l][r][0][1],qsum(1,l-1,1,r-1,1,1,l,r));
//3
add(dp[l][r][1][0],qsum(l+1,m,r+1,m,1,0,l,r));
add(dp[l][r][1][0],qsum(l+1,m,r+1,m,1,1,l,r));
//4
add(dp[l][r][1][1],qsum(l+1,m,1,r-1,1,1,l,r));
add(dp[l][r][1][1],lst);
a[l][r][0][0]=dp[l][r][0][0];
a[l][r][1][0]=dp[l][r][1][0];
a[l][r][0][1]=dp[l][r][0][1];
a[l][r][1][1]=dp[l][r][1][1];
if (fl[i]) add(ans,(dp[l][r][1][1]+dp[l][r][1][0]+dp[l][r][0][1]+dp[l][r][0][0])%mod);
}
lst&=vis[i];
}
}
int main() {
read(n);read(m);
init();
solve();
printf("%lld\n",ans);
return 0;
}
P14364 [CSP-S 2025] 员工招聘
solution:
trick:贡献延后计算
懒得写了,放一篇比较好的题解。
大致就是对于不确定的位置先空着,钦定一个条件,在后面填数的时候考虑贡献。
类似的题目:
AT_arc207_a [ARC207A] Affinity for Artifacts
Code
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
#define ll long long
#define qwq Ff472130
#define f(i,l,r) for (int i=l;i<=r;i++)
#define F(i,l,r) for (int i=l;i>=r;i--)
const int N=500+10;
const int inf=1e9+10;
const int mod=998244353;
inline void add(int &x,int y) {x+=(x+y>=mod)?(y-mod):y;}
inline void read(int &x) {
x=0;
char ch=getchar();
while (ch<48) ch=getchar();
while (ch>=48) x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
}
int n,m,ans;
char s[N];
int a[N],t[N],cnt[N];
int dp[2][N][N];
int fac[N],C[N][N];
inline void init() {
cnt[0]=t[0];fac[0]=1;
f(i,1,n) cnt[i]=cnt[i-1]+t[i];
f(i,1,n) fac[i]=1ll*fac[i-1]*i%mod;
f(i,0,n) {
C[i][0]=1;
f(j,1,i) C[i][j]=(C[i-1][j]+C[i-1][j-1])%mod;
}
}
int main() {
read(n);read(m);
scanf("%s",s+1);
f(i,1,n) read(a[i]),t[a[i]]++;
init();
dp[0][0][0]=1;
f(i,0,n-1) {
const int d0=i&1,d1=d0^1;
f(j,0,i) f(k,0,i) {
if (s[i+1]=='1') {
if (n-cnt[j]>k) add(dp[d1][j][k+1],dp[d0][j][k]);
f(o,0,t[j+1]) {
if (o>k) break;
if (cnt[j]>i-k) add(dp[d1][j+1][k-o],1ll*(cnt[j]-i+k)*dp[d0][j][k]%mod*C[k][o]%mod*C[t[j+1]][o]%mod*fac[o]%mod);
}
}
else {
f(o,0,t[j+1]) {
if (o<=k) add(dp[d1][j+1][k-o+1],1ll*dp[d0][j][k]*C[k][o]%mod*C[t[j+1]][o]%mod*fac[o]%mod);
if (o<=k&&cnt[j+1]>i-k+o) add(dp[d1][j+1][k-o],1ll*(cnt[j+1]-i+k-o)*dp[d0][j][k]%mod*C[k][o]%mod*C[t[j+1]][o]%mod*fac[o]%mod);
}
}
}
memset(dp[d0],0,sizeof(dp[d0]));
}
f(i,0,n-m) add(ans,1ll*dp[n&1][i][n-cnt[i]]*fac[n-cnt[i]]%mod);
printf("%d\n",ans);
return 0;
}
P3336 [ZJOI2013] 话旧
第一道独立做出的黑题。
solution
首先考虑 \(k=0\) 时的方案数。
显然只可能有 \(\frac{n}{2}\) 次上升,最后一次上升后必须选择下降到 \(0\),那么在每次上升后可以选择降到 \(0\) 或者不降到 \(0\),那么对于 \((0,0)\) 到 \((n,0)\) 有 \(2^{\frac{n}{2}-1}\) 种方案。
接下来可以考虑 dp,设 \(dp[i][0/1]\) 表示经过第 \(i\) 个点,前一段斜率为 \(-1/1\) 的方案数,考虑如何在两点间进行转移。
先钦定两点的 \(y\) 坐标都是大于 \(0\) 的,于是对于所有的情况进行分类讨论。
dp[i][1] 可能被转移的情况
- 由 \(dp[i-1][0]\) 转移而来,且触碰到直线 \(y=0\)。
因为上一个点前的斜率为 \(-1\),所以上一个点只能下降到 \(0\) 后再考虑上升,由于当前点前斜率为 \(1\),所以我们从 \(0\) 到当前点这一段方案是唯一的,那么只需要考虑下降到 \(0\) 的点和最后一次碰到 \(0\) 之间的长度的方案即可。
下图中红色线段表示唯一方案,蓝色线段是我们需要考虑的方案。
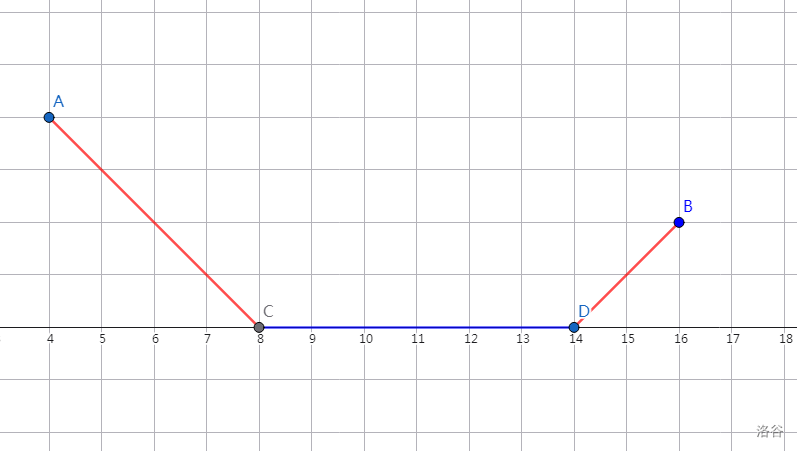
只需要点 \(C\) 和点 \(D\) 之间的方案数即可。
那么这个问题本质上和 \(k=0\) 的时候没有区别,设长度为 \(len\),答案即为 \(2^{\frac{len}{2}-1}\),注意特判 \(len=0\) 是方案数为 \(1\)。
- 由 \(dp[i-1][1]\) 转移而来,且触碰到直线 \(y=0\)。
由于上一个点可以选择继续上升,那么可以转化为若干个上面的情况。
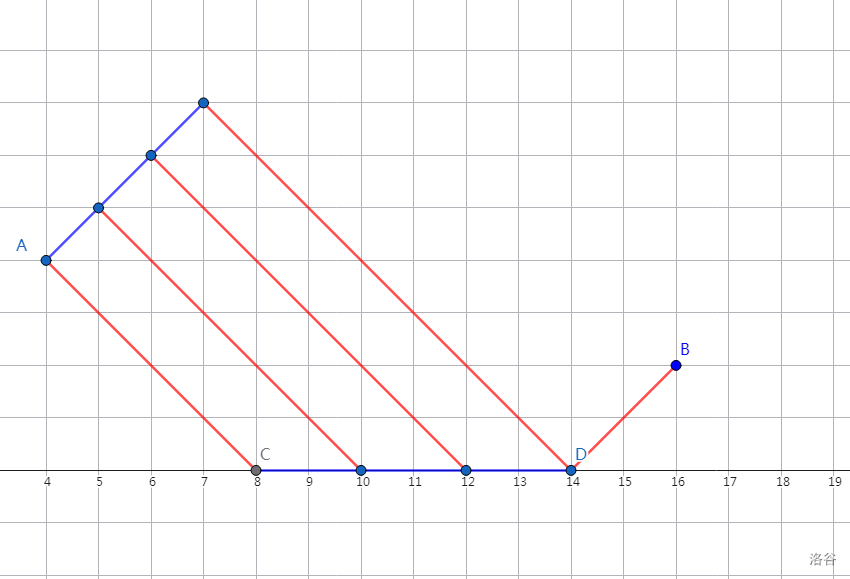
设 \(CD\) 长度为 \(len\)。
比如,\(len=6\),可以向上走的情况转化为 \(len'=6\),\(len'=4\),\(len'=2\),\(len'=0\) 只向下走的情况。方案数即为这几种向下走情况方案数的和。
即为:
\(\begin{aligned}
(\sum^\frac{len}2_{i=1} 2^{i-1})+1 = 2^{\frac{len}2}
\end{aligned}\)
,加 \(1\) 是因为要考虑 \(len'=0\) 的情况。
- 由 \(dp[i-1][1]\) 转移而来,且不触碰到直线 \(y=0\)。
此时需满足条件 \(x_i-x_{i-1}=y_i-y_{i-1}\) 即可,显然方案数只有一种。
dp[i][0] 可能被转移的情况
- 由 \(dp[i-1][0]\) 转移而来,且不触碰到直线 \(y=0\)。
只需满足 \(x_i-x_{i-1}=y_{i-1}-y_i\) 即可,显然方案数只有一种。
- 由 \(dp[i-1][0]\) 转移而来,且触碰到直线 \(y=0\)。
类似于之前 \(dp[i][1]\) 的情况,这时候需要考虑在哪里最后一次碰到 \(0\) 即可。
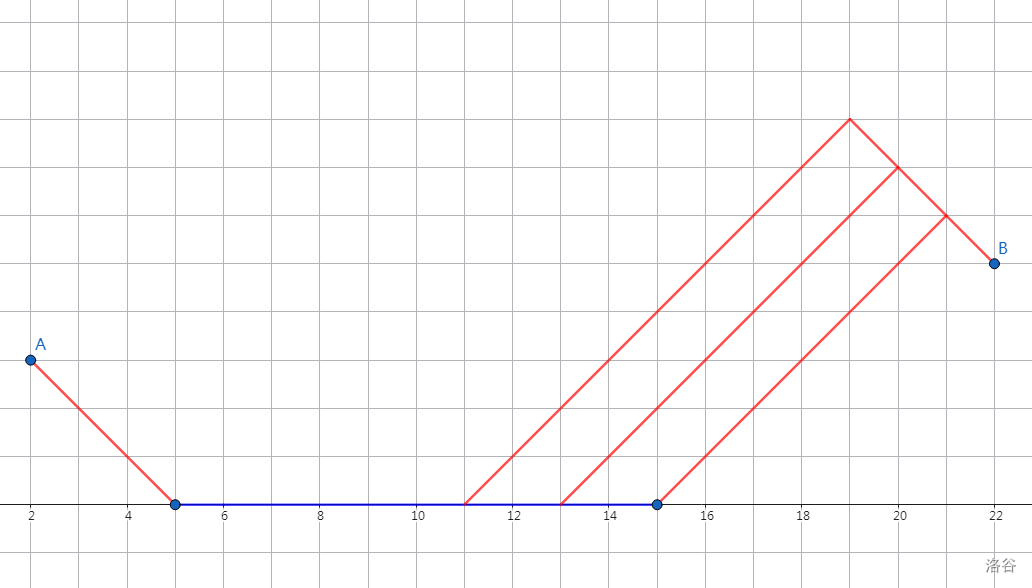
设 \(len=x_i-x_{i-1}-y_i-y_{i-1}-2\),即
图中蓝色线段长度,与 \(dp[i][1]\) 转移时的区别是此处减了 \(2\)。
翻转一下其实和之前的第二种情况类似,需要注意的是这里不可以在 \(len+2\) 时才上升,因为这样只能做到斜率为 \(1\)。
和上面第二种情况同理,方案数为 \(2^{\frac{len}2}\)。
- 由 \(dp[i-1][1]\) 转移而来,且触碰到直线 \(y=0\)。
可以向上走,那么和之前一样,也可以转化为若干种只往下走的情况。
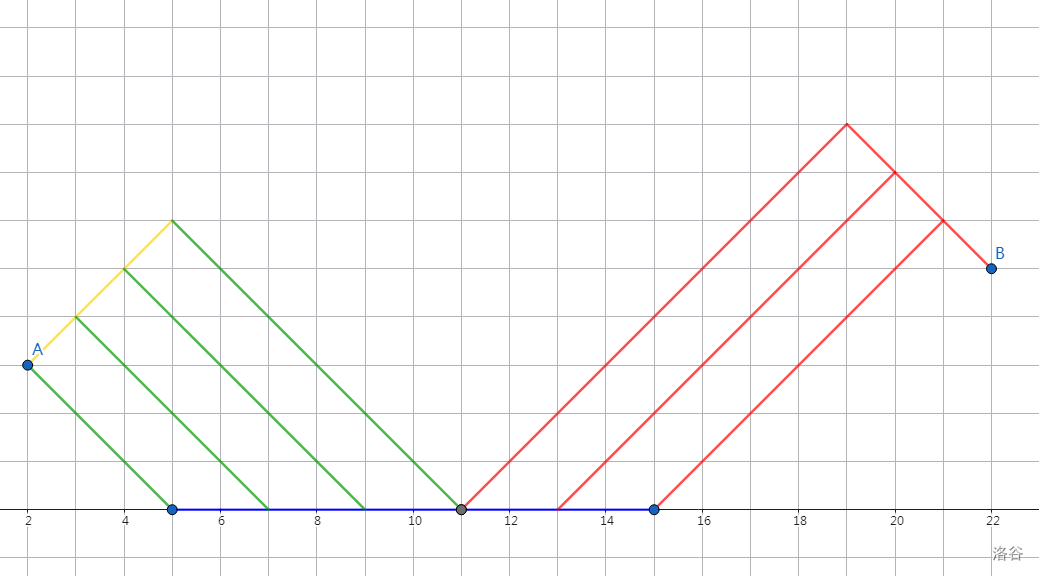
设 \(len=x_i-x_{i-1}-y_i-y_{i-1}-2\)。
方案数为
\(\begin{aligned}
(\sum^\frac{len}2_{i=1} 2^{i-1}) = 2^{\frac{len}2}-1
\end{aligned}\)。
- 由 \(dp[i-1][1]\) 转移而来,且不触碰到直线 \(y=0\)。
只需满足 \(y_i+x_i-x_{i-1}>y_{i-1}\) 即可,显然方案数只有一种。
以上就是所有的转移情况啊呀累死我了,注意当 \(y=0\) 是需要特殊处理,至此第一问结束。
第二问贪心即可,由于由斜率为 \(1\) 经过一个点后必然存在合法方案,所以只需倒着枚举,记录如果斜率为 \(-1\) 经过下一个点有没有合法方案,根据上面的讨论计算相应的最大值即可。
时间复杂度 \(O(k \log n)\)。
Code
#include<cstdio>
#include<algorithm>
using namespace std;
#define ll long long
#define qwq Ff472130
#define f(i,l,r) for (int i=l;i<=r;i++)
#define F(i,l,r) for (int i=l;i>=r;i--)
const int N=1e6+10;
const int inf=1e9+10;
const int mod=19940417;
inline void add(ll &x,int y) {x+=(x+y>=mod)?y-mod:y;}
inline void read(int &x) {
x=0;
char ch=getchar();
while (ch<48) ch=getchar();
while (ch>=48) x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
}
inline ll qpow(ll a,ll b) {
ll res=1;
while (b) {
if (b&1) res=res*a%mod;
a=a*a%mod;
b>>=1;
}
return res;
}
int n,m,ans;
ll dp[N][2];
struct Node{int x,y;}a[N];
inline bool cmp(Node a,Node b) {return a.x<b.x;}
//从(0,0)到(n,0)的方案数
inline ll work0(int n) {
if (n==0) return 1;
if (n<0) return 0;
return qpow(2,n/2-1);
}
inline void solve(int i) {
int len=a[i].x-a[i-1].x-a[i].y-a[i-1].y;
//update:dp[i][1]
if (len>=0) add(dp[i][1],dp[i-1][0]*work0(len)%mod); //1st
if (len>=0) add(dp[i][1],dp[i-1][1]*qpow(2,len/2)%mod); //2nd
if (a[i].x-a[i-1].x==a[i].y-a[i-1].y) add(dp[i][1],dp[i-1][1]); //3rd
//update:dp[i][0]
if (a[i].x-a[i-1].x==a[i-1].y-a[i].y) add(dp[i][0],dp[i-1][0]); //1st
if (len>=2) add(dp[i][0],dp[i-1][0]*qpow(2,(len-2)/2)%mod); //2nd
if (len>=2) add(dp[i][0],dp[i-1][1]*(qpow(2,len/2)-1)%mod); //3rd
if (a[i].x-a[i-1].x!=a[i].y-a[i-1].y) add(dp[i][0],dp[i-1][1]); //4th
}
//从y1=0到y2=0
inline void From_0_to_0(int i) {
int len=a[i].x-a[i-1].x;
add(dp[i][0],dp[i-1][0]*work0(len)%mod);
}
//从y=0的点到y>0的点
inline void From_0(int i) {
int len=a[i].x-a[i-1].x-a[i].y;
//update:dp[i][1]
add(dp[i][1],dp[i-1][0]*work0(len)%mod);
//update:dp[i][0]
if (len>=2) add(dp[i][0],dp[i-1][0]*qpow(2,(len-2)/2)%mod);
}
//从y>0的点到y=0的点,注意此时dp[i][1]不应该有值
inline void To_0(int i) {
int len=a[i].x-a[i-1].x-a[i-1].y;
//update:dp[i][0]
add(dp[i][0],dp[i-1][0]*work0(len)%mod);
add(dp[i][0],dp[i-1][1]*qpow(2,len/2)%mod);
}
inline void solve_1() {
dp[1][0]=1;
f(i,2,m) {
if (a[i-1].y==0&&a[i].y==0) From_0_to_0(i);
else if (a[i-1].y==0) From_0(i);
else if (a[i].y==0) To_0(i);
else solve(i);
}
printf("%d ",dp[m][0]);
}
//斜率为1可行
inline void work_1(int i,bool lst) {
if (lst) {
//下一个点斜率为-1可行
int dx=a[i+1].x-a[i].x,dy=a[i+1].y-a[i].y;
if (dy<0) dy=-dy;
//一直上升然后下降
ans=max(ans,max(a[i].y,a[i+1].y)+(dx-dy)/2);
}
else {
int len=a[i+1].x-a[i].x-a[i+1].y-a[i].y;
//先直接降到0,然后上升len/2,再下降len/2,以斜率为1经过下一个点
ans=max(ans,a[i].y+len/2);
}
}
//斜率为-1可行
inline void work_2(int i,bool lst) {
int len=a[i+1].x-a[i].x-a[i+1].y-a[i].y;
//下降到0后一直上升,到最大合法高度后下降,以斜率为-1经过下一个点
if (lst) ans=max(ans,a[i+1].y+len/2);
//直接降到0,然后上升len/2,再下降len/2,以斜率为1经过下一个点
else ans=max(ans,len/2);
}
//计算当前斜率为-1是否存在合法方案
inline bool work_3(int i,bool lst) {
if (a[i].y==0) return 1;
int len=a[i+1].x-a[i].x-a[i+1].y-a[i].y;
//可以降到0再由斜率为1通过下一个点,必然合法
if (len>=0) return 1;
//下一个点斜率为-1可行并且当前点斜率为-1可以直接碰到下一个点
if (a[i].y-a[i+1].y==a[i+1].x-a[i].x&&lst) return 1;
//否则不可行
return 0;
}
inline void solve_2() {
bool lst=1;
F(i,m-1,1) {
ans=max(ans,a[i].y);
if (dp[i][1]) work_1(i,lst);
if (dp[i][0]) work_2(i,lst);
lst=work_3(i,lst);
}
printf("%d\n",ans);
}
int main() {
read(n);read(m);
f(i,1,m) read(a[i].x),read(a[i].y);
a[++m]={0,0};a[++m]={n,0};
sort(a+1,a+1+m,cmp);
solve_1();
solve_2();
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号