Leetocde的两道丑数题目：264. 丑数 II➕313. 超级丑数

Q：

A：

用变量记录已经✖2、✖3、✖5的元素下标i2、i3、i5。表示截止到i2的元素都已经乘过2（结果添加到序列尾部的意思），i3、i5同理。这样每次可以循环可以O(1)时间找到下一个最小的丑数，时间O(N)，空间O(N)。

class Solution {
public:
    int nthUglyNumber(int n) {
        if(n<=0){
            return 0;
        }
        int i2=0,i3=0,i5=0;
        vector<int> vec={1};
        while(vec.size()<n){
            int min_mul=vec[i2]*2;
            min_mul=min(min_mul,vec[i3]*3);
            min_mul=min(min_mul,vec[i5]*5);
            if(min_mul==vec[i2]*2){
                i2++;
            }
            if(min_mul==vec[i3]*3){
                i3++;
            }
            if(min_mul==vec[i5]*5){
                i5++;
            }
            vec.push_back(min_mul);
        }
        return vec.back();
    }
};

还有一种利用堆的方法，堆初始只有一个元素1，第一次循环：堆顶元素1分别✖2、3、5，结果加入堆，堆顶元素1就是第一个丑数，pop掉。这样堆还剩2、3、5。第二次循环：堆顶元素2分别✖2、3、5，结果加入堆，堆顶元素2就是第二个丑数。
这样循环n次，最终会找到第n个丑数。时间O(NlogN)，空间O(N)。

Q:

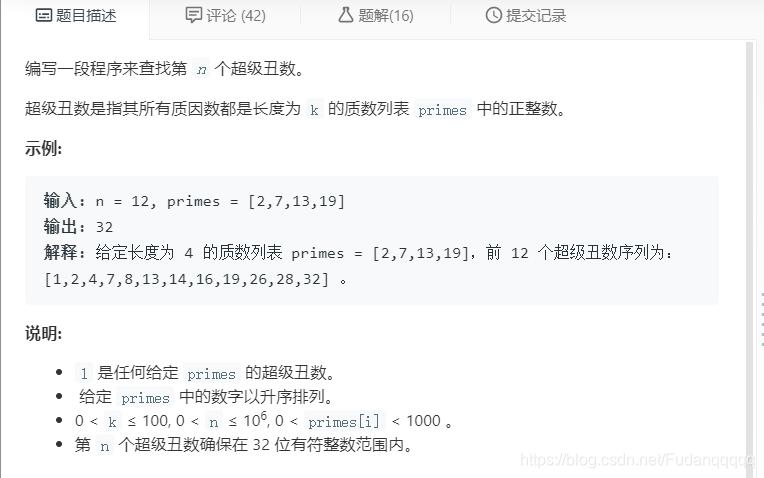
A:

之前是2、3、5，现在是给定了primes.size()个数。那么就建一个数组pos，其中pos[i]指明结果序列中已经乘了primes[i]的最小下标，和上一题类似。

class Solution {
public:
    int nthSuperUglyNumber(int n, vector<int>& primes) {
        if(n<=0){
			return 0;
		}
		vector<int> vec={1};
		vector<int> pos(primes.size(),0);
		while(n>1){
			--n;
			int nex=INT32_MAX;
			for(int i=0;i<primes.size();++i){
				nex=min(nex,vec[pos[i]]*primes[i]);
			}
			for(int i=0;i<primes.size();++i){
				if(nex==vec[pos[i]]*primes[i]){
					pos[i]++;
				}
			}
            vec.push_back(nex);
		}
		return vec.back();
    }
};