<Re:从零开始的算法总结>(2) --并查集
引入--等价类
-
等价关系
设集合A内有n各元素, R是集合 A 上的一个二元关系,若R满足:
自反性:∀ a ∈A, => (a, a) ∈ R
对称性:(a, b) ∈R∧ a ≠ b => (b, a)∈R
传递性:(a, b)∈R,(b, c)∈R =>(a, c)∈R
则称R是定义在A上的一个等价关系。设R是一个等价关系,若(a, b) ∈ R,则称a等价于b,记作 a ~ b
-
等价类
等价类是指相互等价的元素的最大集合,最大意味着不存在类以外的元素与它们等价。且由于每一个元素只能属于一个等价类,所以等价关系把集合A划分为不相交的等价类
-
等价类问题
-
离线等价类问题:已知n和R,确定所有的等价类
-
在线等价类问题(又称为并查集问题):初始有n个元素,每个元素都属于一个独立的等价类,需要执行以下操作:
-
combine(a,b )把包含a和b的等价类合并成一个等价类,其思路如下
classA = find(a); classB = find(b); if(classA!=classB) unite(classA,classB); -
find(theElement),确定元素theElement在哪一个类,目的是确定给定的两个元素是否在同一个等价类
-
-
并查集
-
定义
在一些有N个元素的集合应用问题中,我们通常是在开始时让每个元素构成一个单元素的集合,然后按一定顺序将属于同一组的元素所在的集合合并,其间要反复查找一个元素在哪个集合中。
-
主要操作
- 初始化
把每个点所在集合初始化为其自身。
通常来说,这个步骤在每次使用该数据结构时只需要执行一次,无论何种实现方式,时间复杂度均为O(N)。 - 查找
查找元素所在的集合。 - 合并
将两个元素所在的集合合并为一个集合。
通常来说,合并之前,应先判断两个元素是否属于同一集合,这可用上面的“查找”操作实现。
- 初始化
-
数据结构
并查集算法可以基于数组、链表和森林的方式实现,往往使用森林实现以期获得更好的效率。
在线等价类问题的应用实例
机器调度问题
-
题目信息:某工厂有一台机器能执行n个任务,任务i的开始时间为整数ri ,截止时间为di,在该机器商完成每个任务都需要一个单元的时间,一种可行的调度方案时为每个任务分配相应的时间段,使得分配给任务i的时间正好位于开始时间和截止时间之间。同一个时间段不允许分配给多个任务
-
设计方法
-
- 按开始时间的非递增次序对任务进行排序
-
- 按开始时间的非递增次序考察任务,对于每一个任务,确定一个空闲时间段,这个时间段在截止时间之前,但与截止时间最为接近,如果这个时间段位于任务开始时间之前则分配失败,否则就把这个时间段分配给该任务。
-
-
方法实现:
排序问题不过多解释。2)可进行如下处理
令d为所有任务最后的截止时间,将可用时间段表示为从从 i-1到 i,其中1<=i<=d,称为时间段1到时间段d,对于任意一个时间段a,用near(a)表示空闲时间段i,其中i是在小于等于a范围内最大的i,如果不存在,则定义near(a)=near(0)=0。两个时间段a和b同属于一个等价类,当且仅当near(a)=near(b)。
在任务调度之前,所有时间段都有near(a)=a,即每个时间段哦都是一个独立的等价类,当按步骤2)把时间段a分配给某个任务时,对于所有near(b)=a的时间段b,near(b)的新的near值修改为near(a-1)。
因此,当把时间段a分配给一个任务时,需要对当前包含时间段a和a-1的等价类进行合并。
如果每个等价类e用nearest返回其成员的near值,则near值酱油nearest[find(a)]给出
解决方案
基于数组
使用一个数组equivClass且令equiClass[i]为包含元素i的等价类,在合并两个不同的类时,从两者中人去一个类,然后把该类的所有元素的值修改为另一个类元素的值。
/*
*基于数组实现并查集算法*/
int *equivClass,n;//等价类数组和元素个数
void initialize(int number_of_elements){
n = number_of_elements;
equivClass = new int[n+1];
for (int e = 1; e <= n;e++)
equivClass[e] = e;
}
void unite(int classA,int classB){
//合并类classA和classB
//假设class A!=classB
for (int k = 1; k <= n;k++){
if(equivClass[k]==classB)
equivClass[k] = classA;
}
}
int find(int theElement){
//查找具有元素theElement的类
return equivClass[theElement];
}
基于链表
-
数据结构
结构体equivNode,具有数据成员equivClass、size和next
类型为equivNode的数组node[1:n]用于描述n个元素,每个元素都有一个对应的等价类链表
node[e].equivClass既是find(e)的返回值,也是一个整形指针,指向等价类node[e].equivClass的链表首结点
只有e是链表的首结点才定义node[e].size,这是node[e].size表示从node[e]开始的链表的节点个数
node[e].next给出了包含结点e的链表的下一个节点,因为结点从1到n编号,所以可以用0表示空指针NULL
-
代码实现
typedef struct equivNode{ int equivClass; //元素类标识符 int size; //元素个数 int next; //类中下一个元素的指针 } equivNode; equivNode *node; //节点数组 int n; //元素个数 void initialize(int number_of_elements){ n = number_of_elements; node = new equivNode[n + 1]; for (int e = 1; e <= n;e++){ node[e].equivClass = e; node[e].size = 1; node[e].next = 0; } } void unite(int classA,int classB){ //合并classA和classB //classA和classB是链表首元素 //使classA成为较小的类 if(node[classA].size>node[classB].size) swap(classA,classB); //改变较小的类的equivClass值 int k; for (k = classA; node[k].next != 0;k=node[k].next) node[k].equivClass = classB; //处理最后一个节点 node[classB].equivClass = classB; //在链表classB的首元素后插入链表classA //修改新链表大小 node[classB].size+=node[classA].size; node[k].next = node[classB].next; node[classB].next = classA; } int find(int theElement){ //查找包含元素theElement的类 return node[theElement].equivClass; }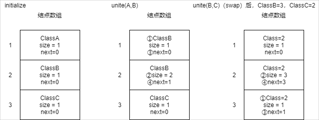
上图表示一个简单的合并过程
算法分析
1次初始化和f次查找的复杂度为O(n+f),对于u此合并,每一次合并的性能为O(较小类的大小),合并过程中,小类移动到打雷,一次合并复杂度为O(移动元素个数),一次合并后心累的大小至少是原来小磊大小的两倍,由于操作结束时没有哪个类的元素数会超过u+1(此为数学结论),所以没有哪个元素元素的移动个数超过u+1,另外最多有2u个元素发生移动(数学结论),因此总移动次数不会超过2ulog2(u+1),综上n次合并复杂度为O(nlogn)
算法优化
按照前述的思路,单次查找的复杂度为O(n),单次合并的平均复杂度为O(logn),但是最坏情况下,复杂度为O(n)。
我们不再通过等价类的方式区分每一项,修改类的方式也不再是修改类标志,而是合并引入一个“祖先”概念模拟并查集。
现在我们假定 f[i] 表示第 i 个人的祖先是谁。
现在我们有甲,乙,丙三个人(分别用 a, b, c 表示)
假设经过考察,乙是甲的祖先。则有 f[a]=b,后来甲又证明是丙的祖先那么有 f[c]=a,
但是如果我们这样表示,丙不能直接知道乙,容易一家人不认一家人
所以,我们必须直接让丙的祖先变成最大的祖先。定义如下find
//优化find
int find(int x){
while(x!=fa[x]) x=fa[x]=fa[fa[x]];
}
再附加额外设定
- 一个人不能有两个祖先。
- 当已经有祖先的人查到更久远的祖先时,祖先也将成为更高祖先的子孙。
例题--洛谷P3367
题目描述
如题,现在有一个并查集,你需要完成合并和查询操作。
输入格式
第一行包含两个整数 N,MN,M ,表示共有 NN 个元素和 MM 个操作。
接下来 MM 行,每行包含三个整数 Zi,Xi,Yi。
当 Zi=1时,将 Xi 与 Yi所在的集合合并。
当 Zi=2时,输出 Xi 与 Yi是否在同一集合内,是的输出 Y ;否则输出 N 。
输出格式
对于每一个 Z_i=2Z**i=2 的操作,都有一行输出,每行包含一个大写字母,为 Y 或者 N 。
代码
//优化前
#include<iostream>
#include<cstdlib>
using namespace std;
int Array[10005];
void unite(int classa,int classb,int n);
void initialize(int n);
int main() {
int m, n,x,y,z;
cin >> n >> m;
initialize(n);
for (int i = 0; i < m; i++) {
cin >>z >> x >> y;
if (z == 1) {
unite(x, y, n);
}
else if(z == 2){
if (find(x) == find(y))
cout << "Y" << endl;
else
cout << "N" << endl;
}
}
}
void initialize(int n) {
for (int i = 1; i <= n; i++) {
Array[i] = i;
}
}
int find(int theElement){
return Array[theElement];
}
void unite(int classA, int classB,int n) {
int a = find(classA);
int b = find(classB);
for (int i = 1; i <= n; i++) {
if (find(i) == b)
Array[i] = a;
}
}
//优化后
#include<iostream>
#include<cstdlib>
using namespace std;
int Array[10005];
int find(int theElement);
void initialize(int n);
int main() {
int m, n,x,y,z;
cin >> n >> m;
initialize(n);
for (int i = 0; i < m; i++) {
cin >>z >> x >> y;
int a = find(x);
int b = find(y);
if (z == 1) {
Array[a]=b;
}
else if(z == 2){
if (a == b)
cout << "Y" << endl;
else
cout << "N" << endl;
}
}
}
void initialize(int n) {
for (int i = 1; i <= n; i++) {
Array[i] = i;
}
}
int find(int theElement) {
while (theElement != Array[theElement]) theElement = Array[theElement] = Array[Array[theElement]];
return theElement;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号