K-D树及其实现
简介
在单个维度的范围搜索场景下,如:搜索创建时间最靠近某个日期的商品信息。可以通过遍历所有的商品信息,计算每个商品的创建日期的差值,得到差值最小的商品即可,这样每次查询的时间复杂度为 \(O(n)\);或者通过构造一个 BST,通过日期进行比较查询,这样查询的时间复杂度为 \(O(log_2n)\)
而对于多个维度的范围搜索,比如在一个二维平面内存在的点集合中查找距离当前点最近的点。同样可以枚举这个集合内的每个点,找到距离最近的点,这样每次查询的时间复杂度依旧为 \(O(n)\);而对于构造的 BST 来讲,则无法通过距离的方式来进行比较构建 BST,因为待查询的点是不确定的
K-D 树是一种支持在多个维度下进行最近距离点搜索的数据结构,在 KNN,以及一些游戏的使用场景中有较多的应用
原理
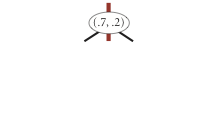
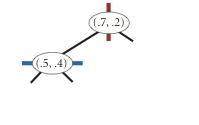
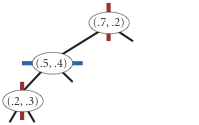
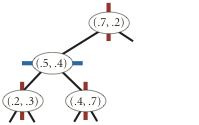
K-D 树的每个非叶子节点都会作为一个空间的超平面的划分点,如,对于二维空间的点,第一层的节点按照 \(x\) 维度进行比较,第二层的节点按照 \(y\) 维度进行比较,第三层再按照 \(x\) 维度……
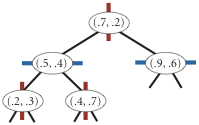
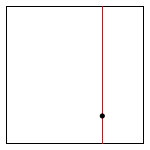
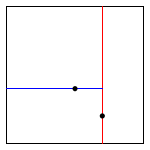
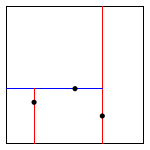
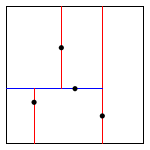
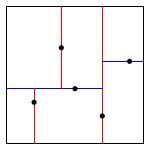
例如,对于一个在二维平面上的一些点:\((0.7,0.2)\),\((0.5,0.4)\),\((0.2,0.3)\),\((0.4,0.7)\),\((0.9,0.6)\),构建 K-D 树的过程如下图所示:
| insert (0.7, 0.2) | insert (0.5, 0.4) | insert (0.2, 0.3) | insert (0.4, 0.7) | insert (0.9, 0.6) |
|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
如果待插入的节点顺序能够很好地均匀地划分每个超平面,那么就会得到一颗类似完全平衡树的树结构。由于 K-D 树的特性,无法通过旋转的方式对树进行重平衡(可以通过类似 AVL 树的旋转方式对节点进行替换)
构造树
如果依次插入的节点能够很均匀地分布在二叉树的节点上,那么得到的树的高度就是 \(log_2N\),这样能够达到很好的查询效率,因此一般在构造 K-D 树的时候会对每个维度选择对应的中位数进行处理,因此构造的时间复杂度主要体现在查找中位数上,通过类似快速排序的思想,可以使得构造整颗树的时间复杂度为 \(O(Nlog_2N)\)
对于插入和删除的操作,由于无法直接通过旋转的方式来达到再平衡的目的,因此一般的处理策略就是在插入或删除一定的节点后,重新构造整颗树,这样使得均摊复杂度为 \(O(log_2N)\)
定义点的类型:
/**
*@author lxh
*/
public abstract class Point
implements Comparable<Point> {
public abstract double distanceSquaredTo(Point point);
}
// 一般情况下的二维平面,我们可以自定义对应的实现
public class Point2D
extends Point {
private final double x; // x coordinate
private final double y; // y coordinate
public Point2D(double x, double y) {
if (Double.isInfinite(x) || Double.isInfinite(y))
throw new IllegalArgumentException("Coordinates must be finite");
if (Double.isNaN(x) || Double.isNaN(y))
throw new IllegalArgumentException("Coordinates cannot be NaN");
if (x == 0.0) this.x = 0.0; // convert -0.0 to +0.0
else this.x = x;
if (y == 0.0) this.y = 0.0; // convert -0.0 to +0.0
else this.y = y;
}
public double x() {
return x;
}
public double y() {
return y;
}
@Override
public double distanceSquaredTo(Point point) {
if (!(point instanceof Point2D)) {
throw new IllegalArgumentException();
}
Point2D that = (Point2D) point;
double dx = this.x - that.x;
double dy = this.y - that.y;
return dx*dx + dy*dy;
}
@Override
public int compareTo(Point point) {
if (!(point instanceof Point2D)) {
throw new IllegalArgumentException();
}
Point2D that = (Point2D) point;
if (this.y < that.y) return -1;
if (this.y > that.y) return +1;
return Double.compare(this.x, that.x);
}
}
由于每次都会划分一个新的超平面,因此我们也需要对应其对应的类型:
/**
* 超平面的类型定义
*
*@author lxh
*/
public abstract class React {
/**
* 根据维度的部分,划分对应的左节点超平面
*
* @param point 当前待处理的点
* @param dimension 当前的划分维度
* @return 经过构造后得到的左超平面
*/
public abstract React buildLeftReact(Point point, int dimension);
/**
* 与 {@link #buildLeftReact(Point, int)} 类似,区别在于构造的是右边的超平面
*
* @param point 当前待处理的点
* @param dimension 当前的划分维度
* @return 经过构造后得到的右超平面
*/
public abstract React buildRightReact(Point point, int dimension);
/**
* 当前超超平面距离点的距离(一般实现可以考虑为 <a href="https://zh.wikipedia.org/wiki/%E6%AC%A7%E5%87%A0%E9%87%8C%E5%BE%97%E8%B7%9D%E7%A6%BB">欧几里得距离</a>)的平方
* 作为返回结果
*
* @param point 当前在查询的点
* @return 当前超超平面距离点的距离
*/
public abstract double distanceSquaredTo(Point point);
/**
* 检查当前的超平面中是否包含当前待查询的点
*
* @param point 待查询的点
* @return 如果当前超平面包含待查询的点,则返回 {@code true}, 否则返回 {@code false}
*/
public abstract boolean contains(Point point);
/**
* 检查当前超平面是否与待查询的超平面相交
*
* @param react 当前待查询的超平面
* @return 如果但那给钱超平面与待查询的超平面相交,则返回 {@code true}, 否则,返回 {@code false}
*/
public abstract boolean intersects(React react);
}
// 对于二位的超平面,我们可以选择如下的实现
/**
*@author lxh
*/
public class React2D
extends React {
private final double xmin, ymin; // minimum x- and y-coordinates
private final double xmax, ymax; // maximum x- and y-coordinates
public React2D(double xmin, double ymin, double xmax, double ymax) {
this.xmin = xmin;
this.ymin = ymin;
this.xmax = xmax;
this.ymax = ymax;
if (Double.isNaN(xmin) || Double.isNaN(xmax)) {
throw new IllegalArgumentException("x-coordinate is NaN: " + toString());
}
if (Double.isNaN(ymin) || Double.isNaN(ymax)) {
throw new IllegalArgumentException("y-coordinate is NaN: " + toString());
}
if (xmax < xmin) {
throw new IllegalArgumentException("xmax < xmin: " + toString());
}
if (ymax < ymin) {
throw new IllegalArgumentException("ymax < ymin: " + toString());
}
}
public double xmin() {
return xmin;
}
public double xmax() {
return xmax;
}
public double ymin() {
return ymin;
}
public double ymax() {
return ymax;
}
@Override
public React buildLeftReact(Point point, int dimension) {
checkParameters(point);
Point2D point2D = (Point2D) point;
if (dimension == KdTree.VERTICAL) {
return new React2D(this.xmin, this.ymin, point2D.x(), this.ymax);
}
return new React2D(this.xmin, this.ymin, this.xmax, point2D.y());
}
@Override
public React buildRightReact(Point point, int dimension) {
checkParameters(point);
Point2D point2D = (Point2D) point;
if (dimension == KdTree.VERTICAL) {
return new React2D(point2D.x(), this.ymin, this.xmax, this.ymax);
}
return new React2D(this.xmin, point2D.y(), this.xmax, this.ymax);
}
@Override
public double distanceSquaredTo(Point point) {
if (!(point instanceof Point2D)) {
throw new IllegalArgumentException("不兼容的点类型: " + (point == null ? null : point.getClass()));
}
Point2D p = (Point2D) point;
double dx = 0.0, dy = 0.0;
if (p.x() < xmin) dx = p.x() - xmin;
else if (p.x() > xmax) dx = p.x() - xmax;
if (p.y() < ymin) dy = p.y() - ymin;
else if (p.y() > ymax) dy = p.y() - ymax;
return dx * dx + dy * dy;
}
@Override
public boolean contains(Point point) {
checkParameters(point);
Point2D p = (Point2D) point;
return (p.x() >= xmin) && (p.x() <= xmax)
&& (p.y() >= ymin) && (p.y() <= ymax);
}
@Override
public boolean intersects(React react) {
checkParameters(react);
React2D that = (React2D) react;
return this.xmax >= that.xmin && this.ymax >= that.ymin
&& that.xmax >= this.xmin && that.ymax >= this.ymin;
}
@Override
public String toString() {
return "[" + xmin + ", " + xmax + "] x [" + ymin + ", " + ymax + "]";
}
private static void checkParameters(React react) {
if (!(react instanceof React2D)) {
throw new IllegalArgumentException("不兼容的矩形类型: " + (react == null ? null : react.getClass()));
}
}
private static void checkParameters(Point point) {
if (!(point instanceof Point2D)) {
throw new IllegalArgumentException("不兼容的点类型: " + (point == null ? null : point.getClass()));
}
}
}
实际的 K-D 树实现:
/**
*@author lxh
*/
public class KdTree {
/*
插入或删除到一定次数后需要重新构建当前 K-D 树
*/
private final static int DEFAULT_BUILD_THRESHOLD = 1000;
public static final int HORIZONTAL = 0; // Y 轴维度(水平方向)
public static final int VERTICAL = 1; // X 轴维度(垂直方向)
public static class Node
implements Comparable<Node> {
public static final Node DEFAULT_DIMESSION_NODE = new Node(null, HORIZONTAL);
private final Point point;
private final int dimension;
private Node left, right;
private Node(Point point, int dimension) {
this.point = point;
this.dimension = dimension;
}
public int nextDimension(int dimension) {
if (dimension == HORIZONTAL) return VERTICAL;
return HORIZONTAL;
}
public double currentDimensionVal(Point point) {
if (!(point instanceof Point2D)) {
throw new IllegalArgumentException();
}
if (this.dimension == VERTICAL) {
return ((Point2D) point).x();
}
return ((Point2D) point).y();
}
@Override
public int compareTo(Node o) {
if (o == null) {
throw new IllegalArgumentException();
}
if (!(this.point instanceof Point2D) || !(o.point instanceof Point2D)) {
throw new IllegalArgumentException();
}
if (this.dimension == VERTICAL) {
return Double.compare(((Point2D) this.point).x(), ((Point2D) o.point).x());
}
return Double.compare(((Point2D) this.point).y(), ((Point2D) o.point).y());
}
}
Node root;
private final List<Point> pointList = new ArrayList<>();
private int modifyCnt = 0;
private int size = 0;
private final int batchSize;
public KdTree() {
this(DEFAULT_BUILD_THRESHOLD);
}
public KdTree(int batchSize) {
this.batchSize = batchSize;
}
public KdTree(double[][] points) {
this(points, DEFAULT_BUILD_THRESHOLD);
}
public KdTree(double[][] points, int batchSize) {
this.batchSize = batchSize;
for (double[] p : points) {
pointList.add(buildPoint(p));
}
this.root = build(null, pointList, 0, points.length - 1);
}
public void insert(double[] point) {
if (point == null) {
throw new IllegalArgumentException();
}
Point buildPoint = buildPoint(point);
this.root = insert(root, buildPoint, defaultDimensionNode().dimension);
modifyCnt++;
size++;
pointList.add(buildPoint);
if (modifyCnt > batchSize) {
modifyCnt = 0;
build(null, pointList, 0, pointList.size() - 1);
}
}
public int size() {
return size;
}
public boolean contains(double[] point) {
return contains(root, buildPoint(point));
}
/**
* 查询在一个矩形区域内所有的点
*
* @param rect 待查询的区间的坐标限制
* @return 矩形区域内的所有的点
*/
public Iterable<Point> range(React rect) {
if (rect == null) {
throw new IllegalArgumentException();
}
List<Point> ans = new ArrayList<>();
range(root, initReact(), rect, ans);
return ans;
}
/**
* 查询在当前的 K-D 树中,距离当前点最近的点
*
* @param point 待查询的点
* @return 当前 K-D 树中距离查询点最近的点
*/
public Point nearest(double[] point) {
if (point == null) {
throw new IllegalArgumentException();
}
return nearest(root, initReact(), buildPoint(point), null, Double.POSITIVE_INFINITY);
}
// 首个节点默认的维度
protected Node defaultDimensionNode() {
return Node.DEFAULT_DIMESSION_NODE;
}
// 从一个 double 数组中转换为节点对应的 Point 对象
protected Point buildPoint(double[] point) {
if (point == null) {
throw new IllegalArgumentException();
}
return new Point2D(point[0], point[1]);
}
// 初始所在的空间,如一个 1 x 1 的正方形,或者更高维度的空间
protected React initReact() {
return new React2D(0, 0, 1, 1);
}
private Node build(Node root, List<Point> points, int left, int right) {
if (points == null) {
throw new IllegalArgumentException();
}
Node dimensionNode = root == null ? defaultDimensionNode() : root;
Node currDimensionNode = new Node(null, dimensionNode.nextDimension(dimensionNode.dimension));
if (left == right) {
return new Node(points.get(left), currDimensionNode.dimension);
}
if (left > right) {
return null;
}
int index = findMidIndex(currDimensionNode, points, left, right);
Node node = new Node(points.get(index), currDimensionNode.dimension);
node.left = build(node, points, left, index - 1);
node.right = build(node, points, index + 1, right);
return node;
}
private void range(Node parent, React baseReact,
React rect, List<Point> list) {
if (parent == null) return;
Point point = parent.point;
if (rect.contains(point)) {
list.add(point);
}
React leftRect = baseReact.buildLeftReact(point, parent.dimension);
React rightRect = baseReact.buildRightReact(point, parent.dimension);
if (rect.intersects(leftRect)) {
range(parent.left, leftRect, rect, list);
}
if (rect.intersects(rightRect)) {
range(parent.right, rightRect, rect, list);
}
}
private Point nearest(Node parent, React react,
Point p, Point closerPoint,
double rawDistance) {
if (parent == null) {
return closerPoint;
}
Point point = parent.point;
double curDistance = p.distanceSquaredTo(point);
if (closerPoint == null || curDistance < rawDistance) {
closerPoint = point;
rawDistance = curDistance;
}
React leftRect = react.buildLeftReact(p, parent.dimension);
React rightRect = react.buildRightReact(p, parent.dimension);
double leftDistance = leftRect.distanceSquaredTo(p);
double rightDistance = rightRect.distanceSquaredTo(p);
/*
如果当前待查询点距离划分的超平面的距离大于当前已经查询到的最近的点的距离,
那么这部分超平面内的点不需要再进行查询
*/
if (leftDistance <= rightDistance) {
if (leftDistance < rawDistance) {
closerPoint = nearest(parent.left, leftRect, p, closerPoint, rawDistance);
rawDistance = closerPoint.distanceSquaredTo(p);
}
if (rightDistance < rawDistance) {
closerPoint = nearest(parent.right, rightRect, p, closerPoint, rawDistance);
}
} else {
if (rightDistance < rawDistance) {
closerPoint = nearest(parent.right, rightRect, p, closerPoint, rawDistance);
rawDistance = closerPoint.distanceSquaredTo(p);
}
if (leftDistance < rawDistance) {
closerPoint = nearest(parent.left, leftRect, p, closerPoint, rawDistance);
}
}
return closerPoint;
}
private boolean contains(Node root, Point point) {
if (root == null) {
return false;
}
Node node = new Node(point, root.dimension);
int comp = root.compareTo(node);
if (comp == 0) return true;
if (comp < 0) {
return contains(root.left, point);
}
return contains(root.right, point);
}
private Node insert(Node root, Point point, int dimension) {
if (root == null) {
return new Node(point, defaultDimensionNode().nextDimension(dimension));
}
Node node = new Node(point, root.dimension);
if (node.compareTo(root) <= 0) {
root.left = insert(root.left, point, root.nextDimension(dimension));
} else {
root.right = insert(root.right, point, root.nextDimension(dimension));
}
return root;
}
private int findMidIndex(Node root, List<Point> points, int left, int right) {
return quickSplit(root, points, left, right);
}
private int quickSplit(Node root, List<Point> points, int left, int right) {
Point cur = points.get(left);
double val = root.currentDimensionVal(cur);
int lo = left + 1, hi = right;
while (true) {
while (lo < right && Double.compare(root.currentDimensionVal(points.get(lo)), val) <= 0) lo++;
while (left < hi && Double.compare(root.currentDimensionVal(points.get(hi)), val) > 0) hi--;
if (lo >= hi) break;
exchange(points, lo, hi);
}
exchange(points, left, hi);
return hi;
}
private void exchange(List<Point> points, int i, int j) {
Point tmp = points.get(i);
points.set(i, points.get(j));
points.set(j, tmp);
}
}
参考:
[1] https://oi-wiki.org/ds/kdt/
[2] https://coursera.cs.princeton.edu/algs4/assignments/kdtree/specification.php


 浙公网安备 33010602011771号
浙公网安备 33010602011771号