动态规划问题（十六）股票买卖问题

问题描述

给你一个数组 price[] 表示一支股票在第 i 天的价格为 price[i]，现在有一些限制条件，要求在这些有限制的条件下求最大的股票收益。

限制条件为以下条件之一：

只允许买卖一次 121. 买卖股票的最佳时机
可以无限制地买卖，在再次购买股票之前必须卖掉手中已有的股票 122. 买卖股票的最佳时机 II
最多买卖两次股票，在再次购买之前必须卖掉手中已有的股票 123. 买卖股票的最佳时机 III
最多买卖 k 次股票，在再次购买之前必须卖掉手中已有的股票 188. 买卖股票的最佳时机 IV
可以无限制的买卖，含有冷冻期（在卖出股票之后的第二天不能再买入股票）309. 最佳买卖股票时机含冷冻期
可以无限制的买卖，买卖股票时包含手续费 714. 买卖股票的最佳时机含手续费

解决思路

参考：https://leetcode.com/problems/best-time-to-buy-and-sell-stock-with-transaction-fee/discuss/108870/Most-consistent-ways-of-dealing-with-the-series-of-stock-problems

使用状态机和动态规划来解决这一类问题

对于当前的股票位置，对于买卖情况来讲，只有三种状态：买入、卖出、不做任何处理。因此，这类问题的状态机形式为：

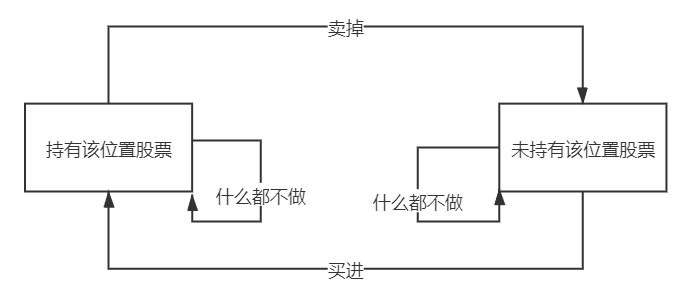
对于当前的某个状态，它能否进行下一步操作取决于两个因素：当前的股票位置、可以进行买卖的次数。因此可以使用一个三维数组来构建一个状态表：fsm[i][k][s] 表示在第 i 天的位置，当可以进行买卖的次数为 k 时，当前股票持有状态为 s 时能够得到的最大收益。由于股票持有状态只能为持有或者没有持有，因此 s=2。

边界情况：

当还没有开始进行股票买卖时，即对第 0 天来讲，当天没有持有股票，当前的收益为 0。即 fsm[0][k][0] = 0
当还没有开始进行股票买卖时，如果持有股票，这是不合理的，因此将它置为最小值。即 fsm[0][k][1] = Integer.MIN_VALUE
当可以买卖的股票次数为 0 时，那么对于任意一天来讲，能够得到的收益都是 0。因此，fsm[i][0][0] = 0
当可以买卖的股票次数为 0，而如果此时持有股票的状态是不可能出现的，因此也需要将它置为最小值。即 fsm[i][0][1] = Integer.MIN_VALUE

转换方程：

对于任意的位置，当前没有持有股票的状态转换方程如下所示：

\[T[i][k][0] = max(T[i - 1][k][0], T[i-1][k][1] + price[i]) \]
解释：当前没有持有股票只能有两种情况：一是之前手上没有股票，今天也不买入这支股票；二是将之前手上持有的股票卖掉，因此需要加上持有的股票的价值。（注意问题描述中将的是一支股票的价格，因此当前股票的价值就是当前位置的股票价值）
在当前位置持有股票的状态转换方程如下：

\[T[i][k][1] = max(T[i - 1][k][1], T[i - 1][k - 1][0] - price[i]) \]
解释：当前位置持有股票只能由两种情况演变而来：一是之前手上持有股票，今天也不卖掉；二是之前手上没有这支股票，现在买入，因此需要减去当前的股票价值。（由于买入会使用一次买票机会，因此这里需要对 k 进行减一操作。当然，在卖出时在进行减一操作也是可以的。

对上文出现的情况进行解释：

只允许买卖一次
- 此时 k=1，执行上文的转换方程即可
可以无限制地买卖，在再次购买股票之前必须卖掉手中已有的股票
- 此时 k=+Infinity，按照无穷大的规则，k = k -1，因此，上面的持有股票的转换方程为：
  \[T[i][k][1] = max(T[i - 1][k][1], T[i - 1][k][0] - price[i]) \]
最多买卖两次股票，在再次购买之前必须卖掉手中已有的股票
- 此时 k=2，执行上文的转换方程即可
最多买卖 k 次股票，在再次购买之前必须卖掉手中已有的股票
- 此时 k 已经给出，直接执行上文的转换方程即可
可以无限制的买卖，含有冷冻期（在卖出股票之后的第二天不能再买入股票）
- 此时 k 的情况与第二种情况一致
- 此时的持有股票来源需要进行一下变换，由于存在一个冷冻期，因此需要从前前一日的状态进行转换，此时持有股票的转换方程为：
  
  \[T[i][k][1] = max(T[i - 1][k][1], T[i - 2][k][0] - price[i]) \]
可以无限制的买卖，买卖股票时包含手续费
- 此时 k 的情况与第二种情况一致
- 以上文的转换方程实现即可，只需要在每次买入时添加额外的手续费即可

实现

只允许买卖一次

public class Solution {
    public int maxProfit(int[] prices) {
        final int N = prices.length;
        final int k = 1;
        int[][][] fsm = new int[N + 1][k + 1][2];

        fsm[0][k][0] = 0;
        fsm[0][k][1] = Integer.MIN_VALUE;

        for (int i = 1; i <= N; ++i) {
            fsm[i][0][0] = 0;
            fsm[i][0][1] = Integer.MIN_VALUE;
        }

        for (int i = 1; i <= N; ++i) {
            fsm[i][k][0] = Math.max(
                fsm[i - 1][k][0], 
                fsm[i - 1][k][1] + prices[i - 1]
            );

            fsm[i][k][1] = Math.max(
                fsm[i - 1][k][1], 
                fsm[i - 1][k - 1][0] - prices[i - 1]
            );
        }

        return fsm[N][k][0];
    }
}

进行空间压缩：

public class Solution {
    public int maxProfit(int[] prices) {
        final int N = prices.length;

        int fsm_i_k_0 = 0, fsm_i_k_1 = Integer.MIN_VALUE;
        for (int price : prices) {
            fsm_i_k_0 = Math.max(fsm_i_k_0, fsm_i_k_1 + price);
            fsm_i_k_1 = Math.max(fsm_i_k_1, -price);
        }

        return fsm_i_k_0;
    }
}

可以无限制地买卖，在再次购买股票之前必须卖掉手中已有的股票

public class Solution {
    public int maxProfit(int[] prices) {
        final int N = prices.length;
        final int k = 1;

        int[][][] fsm = new int[N + 1][k + 1][2];

        fsm[0][k][0] = 0;
        fsm[0][k][1] = Integer.MIN_VALUE;

        for (int i = 1; i <= N; ++i) {
            fsm[i][0][0] = 0;
            fsm[i][0][1] = Integer.MIN_VALUE;
        }

        for (int i = 1; i <= N; ++i) {
            fsm[i][k][0] = Math.max(
                fsm[i - 1][k][0],
                fsm[i - 1][k][1] + prices[i - 1]
            );

            fsm[i][k][1] = Math.max(
                fsm[i - 1][k][1],
                fsm[i - 1][k][0] - prices[i - 1]
            );
        }

        return fsm[N][k][0];
    }
}

进行空间压缩：

public class Solution {
    public int maxProfit(int[] prices) {
        final int N = prices.length;

        int fsm_i_k_0 = 0, fsm_i_k_1 = Integer.MIN_VALUE;
        for (int i = 1; i <= N; ++i) {
            int tmp = fsm_i_k_0;

            fsm_i_k_0 = Math.max(fsm_i_k_0, fsm_i_k_1 + prices[i - 1]);
            fsm_i_k_1 = Math.max(fsm_i_k_1, tmp - prices[i - 1]);
        }

        return fsm_i_k_0;
    }
}

最多买卖两次股票，在再次购买之前必须卖掉手中已有的股票

public class Solution {
    public int maxProfit(int[] prices) {
        final int N = prices.length;
        final int k = 2;
        
        int[][][] fsm = new int[N + 1][k + 1][2];

        fsm[0][1][0] = 0;
        fsm[0][1][1] = Integer.MIN_VALUE;
        fsm[0][2][0] = 0;
        fsm[0][2][1] = Integer.MIN_VALUE;

        for (int i = 1; i <= N; ++i) {
            fsm[i][0][0] = 0;
            fsm[i][0][1] = Integer.MIN_VALUE;
        }

        for (int i = 1; i <= N; ++i) {
            fsm[i][1][0] = Math.max(
                fsm[i - 1][1][0],
                fsm[i - 1][1][1] + prices[i - 1]
            );

            fsm[i][1][1] = Math.max(
                fsm[i - 1][1][1],
                fsm[i - 1][0][0] - prices[i - 1]
            );

            fsm[i][2][0] = Math.max(
                fsm[i - 1][2][0],
                fsm[i - 1][2][1] + prices[i - 1]
            );

            fsm[i][2][1] = Math.max(
                fsm[i - 1][2][1],
                fsm[i - 1][1][0] - prices[i - 1]
            );
        }

        return fsm[N][k][0];
    }
}

进行空间压缩：

public class Solution {
    public int maxProfit(int[] prices) {
        final int N = prices.length;

        int fsm_i_10 = 0, fsm_i_11 = Integer.MIN_VALUE;
        int fsm_i_20 = 0, fsm_i_21 = Integer.MIN_VALUE;
        for (int i = 1; i <= N; ++i) {
            fsm_i_20 = Math.max(fsm_i_20, fsm_i_21 + prices[i - 1]);
            fsm_i_21 = Math.max(fsm_i_21, fsm_i_10 - prices[i - 1]);

            fsm_i_10 = Math.max(fsm_i_10, fsm_i_11 + prices[i - 1]);
            fsm_i_11 = Math.max(fsm_i_11, -prices[i - 1]);
        }

        return fsm_i_20;
    }
}

最多买卖 k 次股票，在再次购买之前必须卖掉手中已有的股票

public class Solution {
    public int maxProfit(int k, int[] prices) {
        final int N = prices.length;

        int[][][] fsm = new int[N + 1][k + 1][2];
        
        for (int i = 1; i <= N; ++i) {
            fsm[i][0][0] = 0;
            fsm[i][0][1] = Integer.MIN_VALUE;
        }

        for (int i = 0; i <= k; ++i) {
            fsm[0][i][0] = 0;
            fsm[0][i][1] = Integer.MIN_VALUE;
        }

        for (int i = 1; i <= N; ++i) {
            for (int j = 1; j <= k; ++j) {
                fsm[i][j][0] = Math.max(
                    fsm[i - 1][j][0],
                    fsm[i - 1][j][1] + prices[i - 1]
                );

                fsm[i][j][1] = Math.max(
                    fsm[i - 1][j][1],
                    fsm[i - 1][j - 1][0] - prices[i - 1]
                );
            }
        }

        return fsm[N][k][0];
    }
}

含有冷冻期（在卖出股票之后的第二天不能再买入股票）

public class Solution {
    public int maxProfit(int[] prices) {
        final int N = prices.length;
        final int k = 2;

        int[][][] fsm = new int[N + 1][k + 1][2];
        fsm[0][k][0] = 0;
        fsm[0][k][1] = Integer.MIN_VALUE;

        for (int i = 1; i <= N; ++i) {
            fsm[i][k][0] = Math.max(
                fsm[i - 1][k][0],
                fsm[i - 1][k][1] + prices[i - 1]
            );

            if (i == 1) {
                fsm[i][k][1] = Math.max(
                    fsm[i - 1][k][1],
                    fsm[i - 1][k][0] - prices[i - 1]
                );

                continue;
            }

            fsm[i][k][1] = Math.max(
                fsm[i - 1][k][1],
                fsm[i - 2][k][0] - prices[i - 1]
            );
        }

        return fsm[N][k][0];
    }
}

进行空间压缩：

public class Solution {
    public int maxProfit(int[] prices) {
        final int N = prices.length;

        int fsm_ik0 = 0, fsm_ik0_pre = 0;
        int fsm_ik1 = Integer.MIN_VALUE;

        for (int i = 1; i <= N; ++i) {
            int fsm_ik0_old = fsm_ik0;

            fsm_ik0 = Math.max(fsm_ik0, fsm_ik1 + prices[i - 1]);
            fsm_ik1 = Math.max(fsm_ik1, fsm_ik0_pre - prices[i - 1]);

            fsm_ik0_pre = fsm_ik0_old;
        }

        return fsm_ik0;
    }
}

买卖股票时包含手续费

public class Solution {
    public int maxProfit(int[] prices, int fee) {
        final int N = prices.length;
        final int k = 2;

        int[][][] fsm = new int[N + 1][k + 1][2];
        fsm[0][k][0] = 0;
        fsm[0][k][1] = Integer.MIN_VALUE;

        for (int i = 1; i <= N; ++i) {
            fsm[i][k][0] = Math.max(
                fsm[i - 1][k][0],
                fsm[i - 1][k][1] + prices[i - 1]
            );

            fsm[i][k][1] = Math.max(
                fsm[i - 1][k][1],
                fsm[i - 1][k][0] - prices[i - 1] - fee
            );
        }

        return fsm[N][k][0];
    }
}

进行空间压缩：

public class Solution {
    public int maxProfit(int[] prices, int fee) {
        final int N = prices.length;

        int fsm_ik0 = 0, fsm_ik1 = Integer.MIN_VALUE;
        for (int i = 1; i <= N; ++i) {
            int fsm_ik0_old = fsm_ik0;
            fsm_ik0 = Math.max(fsm_ik0, fsm_ik1 + prices[i - 1]);
            fsm_ik1 = Math.max(fsm_ik1, fsm_ik0_old - prices[i - 1] - fee);
        }

        return fsm_ik0;
    }
}

posted @ 2021-09-22 16:12 FatalFlower 阅读(99) 评论(0) 收藏举报

刷新页面返回顶部

FatalFlower

动态规划问题（十六）股票买卖问题

问题描述

解决思路

实现

公告