panda复赛押题题解
也是补完了啊,类似我了。
A
第一题就爆炸我写牛魔呢
纯粹数学题,设 \(c = abs(a-b)\),我们继续观察从 \(1\) 开始的连续正整数的和,并且将放在 \(a\) 上设为 \(+i\),将放在 \(b\) 上设为 \(-i\)。(当然这些都是对于 \(c\) 而言)不难发现会有如下的情况:
然后根据奇偶变化的规律,不难发现我们选择这串数字里任何一个数字放在 \(b\) 上都不会影响其原本和的奇偶性,并且我们发现,因为是连续正整数,所以可以有 \(-2 \to -4 \to -6\dots\),可以让原本的和 \(sum_{tot}\) 在 \([0, sum_{tot}]\) 这个区间内到达所有跟和它相同奇偶性的数字。
所以懂了吗,我们只需要提前处理所有连续和,然后二分查找距离 \(c\) 最近的连续和,然后往后找奇偶性相同的就行,不过记得看看当前这个是否符合奇偶性就行。
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define ull unsigned long long
const int N = 5e4+100;
vector <ll> pre(N+1);
void solve () {
int a, b; cin >> a >> b;
int v = abs(a-b);
if (a == b) { cout << "0\n"; return; }
int n = lower_bound(pre.begin()+1, pre.end(), v)-pre.begin();
while ((pre[n]^v)&1) ++n;
cout << n << "\n";
}
int main () {
freopen("equal.in", "r", stdin);
freopen("equal.out", "w", stdout);
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
int _ = 1; cin >> _;
for (int i = 1;i <= N;i++) pre[i] = pre[i-1] + i;
while (_--) solve();
return 0;
}
B
我勒个炸弹啊,原题一字不改啊,直接模拟就完事了。
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int R = 1e3+100;
const int C = 1e3+100;
void read(int &x){
int f=1;x=0;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9') {x=x*10+ch-'0';ch=getchar();}
x*=f;
}
int r, c, maxn;
char s[R][C], mp[R][C];
bool check[R][C];
int main() {
freopen("boom.in", "r", stdin);
freopen("boom.out", "w", stdout);
read(r);read(c);
// cout << r << " " << c << endl;
for (int i = 1;i <= r;i++) scanf("%s", s[i]+1);
for (int i = 1;i <= r;i++)
for (int j = 1;j <= c;j++) {
int num = 0;
if (s[i][j] >= '0' && s[i][j] <= '9') {
num = (int)(s[i][j]-'0');
for (int x = -num;x <= num;x++)
for (int y = abs(x)-num;y <= num-abs(x);y++) {
int tx = i+x;
int ty = j+y;
if (tx <= 0 || ty <= 0 || tx > r || ty > c) continue;
mp[tx][ty] = '.';
check[tx][ty] = true;
}
}
}
for (int i = 1;i <= r;i++) {
for (int j = 1;j <= c;j++) {
if (check[i][j]) cout << mp[i][j];
else cout << s[i][j];
}
cout << endl;
}
return 0;
}
C
其实挺好想的,我们不难发现我们只会让一个物品被买多次,如果有两个物品被买多次,那我把两个物品都只买一次,然后把省下的次数都给那个 \(b_i\) 更大的肯定更优。
所以我们只需要枚举每一数字的 \(b_i\),然后二分出现的比他大的 \(a_i\),然后来算就行了。
可能会问,为什么不直接选择 \(b_i\) 最大的,因为有购买物品数量限制的原因,如果数量足够大这个肯定是可以的,但是我们不难发现因为只能买一个物品多次,所以我们会在多条函数直线中选择,发现这些直线相交的位置都不一样,也会因为购买数量的多少有不同的贡献大小关系,导致答案可能不是最优的。发现数据量较小,所以我们干脆直接枚举一遍。
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define ull unsigned long long
#define pii pair <ll, ll>
void solve () {
ll n, m; cin >> n >> m;
vector <pii> a(m+1);
vector <ll> sum(m+1, 0), b(m+1);
ll ans = 0, maxn = 0;
for (ll i = 1;i <= m;i++)
cin >> a[i].first >> a[i].second;
sort(a.begin()+1, a.end());
for (int i = 1;i <= m;i++) {
// if (!i) sum[i] = a[i].first;
sum[i] = sum[i-1] + a[i].first;
b[i] = a[i].first;
}
for (int i = 1;i <= m;i++) {
int now = a[i].second;
int pos = lower_bound(b.begin()+1, b.end(), now) - b.begin() - 1;
int chose = m-pos;
if (chose >= n) ans = max(ans, sum[m]-sum[m-n]);
else if (pos < i) ans = max(ans, (ll)sum[m]-sum[pos]+(ll)(n-chose)*now);
else ans = max(ans, sum[m]-sum[pos]+a[i].first+(ll)(n-chose-1)*now);
}
cout << ans << "\n";
// sort(b.begin(), b.end());
// for (int i = 1;i < m;i++) {
// if (!i) sum[i] = b[i];
// else sum[i] = sum[i-1] + b[i];
// }
// ll cnt = lower_bound(b.begin(), b.end(), maxn) - b.begin();
// cout << "[+] " << cnt << "\n";
// // ll cnt = 1;
//
// if (!cnt) {
// if (m > n) ans = sum[m-1] - sum[m-n-1];
// else {
// ll tmp = sum[m-1]; ans += tmp;
// n -= m; ans += (ll)n*maxn;
// }
// } else {
// ll tmp = (sum[m-1]-sum[cnt-1]); ans += tmp; n -= ((m-1)-(cnt-1));
// cout << "[----] " << ans << "\n";
// if (fir >= maxn) ans += (ll)n*maxn;
// else n--, ans += fir, ans += (ll)n*maxn;
// }
// cout << ans << "\n";
}
int main () {
freopen("flower.in", "r", stdin);
freopen("flower.out", "w", stdout);
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
ll _ = 1; cin >> _;
while (_--) solve();
return 0;
}
D
很简单的一题,二分加枚举前缀和即可。
不难发现因为位置的大小关系,假设前 \(i\) 个位置小于目标位置,后 \(j\) 个位置大于目标位置,式子可以如下变化:
然后我们用分配律在处理一下式子就不难发现,我们只需要维护两个前缀和,二分与当前目标最近的分割点就行了。
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define ull unsigned long long
#define pii pair <ll, ll>
#define fir first
#define sec second
const ll INF = 1e9+100;
void solve () {
ll n, q; cin >> n >> q;
// cin >> n >> q;
vector <pii> vil(n); vector <ll> p(q);
vector <ll> _1(n+1, 0), _2(n+1, 0), c(n);
for (ll i = 0;i < n;i++) cin >> vil[i].fir >> vil[i].sec;
for (ll i = 0;i < q;i++) cin >> p[i];
sort(vil.begin(), vil.end(), [&](pii x, pii y) -> bool { return x.sec < y.sec; });
// cout << n << "\n";
for (ll i = 0;i < n;i++) {
c[i] = vil[i].sec;
// cout << vil[i].fir << "----" << vil[i].sec << "\n";
_1[i+1] = _1[i] + vil[i].fir, _2[i+1] = _2[i] + vil[i].fir*vil[i].sec;
}
// ll ans = INF;
for (auto tmp : p) {
ll pos = lower_bound(c.begin(), c.end(), tmp)-c.begin();
// cout << "[+] " << pos << "\n";
ll ansl = tmp*_1[pos]-_2[pos], ansr = _2[n]-_2[pos]-tmp*(_1[n]-_1[pos]);
// cout << ansl << "[[[[[]]]]] " << ansr << "\n";
cout << ansl+ansr << "\n";
}
}
int main () {
freopen("distance.in", "r", stdin);
freopen("distance.out", "w", stdout);
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
ll _ = 1;
while (_--) solve();
return 0;
}
E
比较好的一道 \(dp\)。
主观难度大于 \(F\).
这里考虑动态规划(其实这题动态规划还是很好想得),设\(dp_{i, j}\) 表示用 \(j\) 走了 \(i\) 段,那么其实不难想到转移方程:
但是我们还要去记录方案数和字典序最小路径,考虑到这个题它的路径长度都是 \(t\),所以我们的想法就是尽可能地停留,这样子我们在前边到达的节点就是小的,所以可以考虑每次更新状态的之后都尽量的停留。(因为 \(dp\) 在一行中是一个单调不减的序列,所以可以放心更新)
方案数的话我们不难发现,其实就是和最小答案相等的 \(dp_{n, [n, t]}\) 对应的 \(cnt_{n, [n, t]}\) 的 \(\sum\)。
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define ull unsigned long long
#define pll pair <ll, ll>
const ll INF = 2e18+10000;
const int MOD = 123456789;
const int N = 1e3+100;
ll dp[N][N], cnt[N][N], pos[N];
pll pre[N][N];
void solve () {
int n, t; cin >> n >> t;
vector <int> d(n+1), c(t+1);
for (int i = 1;i <= n;i++) cin >> d[i];
for (int i = 1;i <= t;i++) cin >> c[i];
// vector <vector <ll>> dp(n+1, vector <ll>(t+1, INF)),
// cnt(n+1, vector <ll>(t+1));
// vector <vector <pll>> pre(n+1, vector <pll>(t+1));
// vector <int> pos(t+1);
memset(dp, 0x3f, sizeof(dp));
dp[0][0] = 0, cnt[0][0] = 1, pre[0][0] = {0, 0};
for (int j = 1;j <= t;j++) {
for (int i = 0;i <= n;i++) {
if (dp[i][j-1] < dp[i][j]) {
dp[i][j] = dp[i][j-1];
cnt[i][j] = cnt[i][j-1] % MOD;
pre[i][j] = {i, j-1};
} else if (dp[i][j-1] == dp[i][j]) {
cnt[i][j] += cnt[i][j-1];
cnt[i][j] %= MOD;
}
if (i >= 1) {
ll tmp = dp[i-1][j-1] + d[i]*c[j];
if (tmp < dp[i][j]) {
dp[i][j] = tmp;
cnt[i][j] = cnt[i-1][j-1] % MOD;
pre[i][j] = {i-1, j-1};
} else if (tmp == dp[i][j]) {
cnt[i][j] += cnt[i-1][j-1];
cnt[i][j] %= MOD;
pre[i][j] = {i-1, j-1};
}
}
}
}
ll sum = 0, ans = INF, date = n;
for (int j = n;j <= t;j++) {
if (dp[n][j] < ans) ans = dp[n][j], date = j, sum = cnt[n][j];
else if (dp[n][j] == ans) date = j, sum = (sum + cnt[n][j]) % MOD;
}
int i = n, j = date;
while (i && j) {
pos[j] = i;
auto [fi, fj] = pre[i][j];
i = fi, j = fj;
}
cout << ans << "\n" << sum << "\n";
for (int i = date+1;i <= t;i++) pos[i] = n;
for (int i = 1;i <= t;i++) cout << pos[i] << " ";
cout << "\n";
}
int main () {
freopen("move.in", "r", stdin);
freopen("move.out", "w", stdout);
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
int _ = 1;
while (_--) solve();
return 0;
}
F
一道经典的图论。
一开始的确很好想到拓扑,但是这样只能有 80pts,我已经试过了。
首先为什么拓扑不对,如果按照拓扑来想,那么我们就会给每一个点定了一个已经固定的假想的排名,但实际上每一个学生的排名是在一个区间内的,这就会导致我们会遗漏一些人的排名。如图:
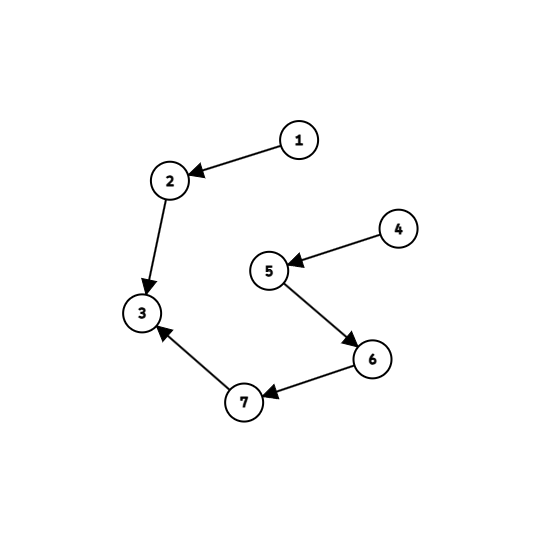
所以我们考虑将提及的点堆起来构成一个新的图,然后正着和反着 \(bfs\) 一遍去得到比它小的点来得到它的排名区间即可。
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define ull unsigned long long
#define pii pair <int, int>
const int N = 1e3+100;
struct R {
int u, v, lst;
}road[N<<1], road2[N<<1];
void solve () {
int n, m, q, tot = 0, tot2 = 0, id = 0; cin >> n >> m >> q;
vector <int> final(n+1), in(n+1), out(n+1), re(n+1), pre(n+2), suf(n+2), f2(n+1);
map <int, int> mp;
auto add = [&](int u, int v) -> void { road[++tot].u = u, road[tot].v = v, road[tot].lst = final[u], final[u] = tot; };
auto add2 = [&](int u, int v) -> void { road2[++tot2].u = u, road2[tot2].v = v, road2[tot2].lst = f2[u], f2[u] = tot2; };
int cnt = 0;
for (int i = 1;i <= m;i++) {
int a, b, c; cin >> a >> b >> c;
cnt += (mp[a] == 0); cnt += (mp[b] == 0);
if (!mp[a]) mp[a] = ++id, re[id] = a;
if (!mp[b]) mp[b] = ++id, re[id] = b;
if (c) add(mp[a], mp[b]), add2(mp[b], mp[a]);
else add(mp[b], mp[a]), add2(mp[a], mp[b]);
}
if (cnt < q) { cout << "NO\n"; return; }
auto bfs = [&](int s) -> void {
vector <bool> vis(n+1, false);
queue <int> q;
q.push(s); vis[s] = true;
while (!q.empty()) {
int fr = q.front(); q.pop();
// vis[fr] = true;
for (int i = final[fr];i;i = road[i].lst) {
int to = road[i].v;
if (!vis[to]) q.push(to), vis[to] = true;
}
}
ll _1 = 0;
for (int i = 1;i <= id;i++) if (vis[i]) ++_1, vis[i] = false;
suf[s] = _1-1; _1 = 0;
q.push(s); vis[s] = true;
while (!q.empty()) {
int fr = q.front(); q.pop();
for (int i = f2[fr];i;i = road2[i].lst) {
int to = road2[i].v;
if (!vis[to]) q.push(to), vis[to] = true;
}
}
for (int i = 1;i <= id;i++) if (vis[i]) _1++, vis[i] = false;
pre[s] = _1-1; _1 = 0;
};
vector <int> ans;
for (int i = 1;i <= id;i++) {
bfs(i);
int l = pre[i] + 1, r = id-suf[i];
if (l <= q && r >= q) ans.push_back(re[i]);
}
if (ans.empty()) { cout << "NO\n"; return; }
sort(ans.begin(), ans.end());
cout << ans.size() << "\n";
for (auto tmp : ans) cout << tmp << " ";
cout << "\n";
}
// vector <vector <int>> ans(n+1, vector <int>(n));
// set <int> ans[N];
// auto topo = [&]() -> void {
// queue <pii> qu;
// vector <bool> vis(n+1);
// vector <int> so(n+1, 0);
// for (int i = 1;i <= n;i++)
// if (!in[i] && out[i]) qu.push({i, 1}), vis[i] = true, so[i] = 1;
// // cout << qu.size() << "\n";
// while (!qu.empty()) {
// auto [fir, sec] = qu.front(); qu.pop();
// ans[sec].insert(fir);
// for (int i = final[fir];i;i = road[i].lst) {
// int to = road[i].v;
// so[to] = max(so[to], sec+1);
// in[to]--;
// if (!in[to]) {
// qu.push({to, so[to]});
// vis[to] = true;
// }
// }
// }
// };
// // topo();
// if (!ans[q].size()) { cout << "NO\n"; return; }
// else {
// cout << ans[q].size() << "\n";
// // sort(ans[q].begin(), ans[q].end());
// for (auto tmp : ans[q]) cout << tmp << " ";
// cout << "\n";
// }
// }
int main () {
freopen("search.in", "r", stdin);
freopen("search.out", "w", stdout);
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
int _ = 1; while (_--) solve();
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号