CF1654G Snowy Mountain 题解

题目链接

点击打开链接

题目解法

很牛的题

显然可以 \(O(n)\) 多源 \(bfs\) 求出 \(h_i\)

考虑从 \(st\) 开始最优的操作是什么？先延最短路径到 \(p\)，然后找到 \(p\) 的相邻点 \(q\)，满足 \(h_p=h_q\)，在 \(p,q\) 之间横跳，耗完所有动能，然后直接滑下去（不经过高度相同的点）
为什么到 \(p\) 之前不会横跳？因为之前横跳会耗费动能，使之后能走到的点集变小，而在 \(p\) 可以横跳无数次，所有只在 \(p\) 横跳不劣（下面称 \(p\) 为平台）
考虑在 \(p\) 横跳的距离是什么？显然为 \(2h_{st}-h_p\)
我们目标是对于每个 \(st\)，找到最小的 \(p\)，使得能从 \(st\) 走到 \(p\)

这咋做？
考虑枚举平台 \(p\)，需要求出 \(d_i\) 表示从 \(i\) 开始能到 \(p\) 的最小动能
转移显然：\(d_j+1\Rightarrow d_i(h_i=h_j),\;d_j-1\Rightarrow d_i(h_i=h_j+1)\)
但这不能直接 \(bfs\)，需要钦定转移顺序
按 \(h_i\) 从小往大转移，不同层之间转移式显然的，现在需要处理的是 \(h\) 相同的点之间的转移，这可以通过树形 \(dp\) 简单求出

考虑如何优化？
考虑对于 \(h_i=h_j\) 的平台，它一定会产生 \(2\) 个长度为 \(h_i\) 的路径
考虑如何说明路径之间不交？
如果路径交，那么只有可能是包含关系，就是下面的情况（满足 \(h_i=h_j,\;h_x=h_y\)）：

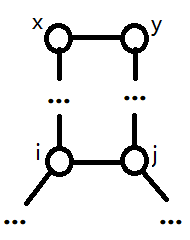
但这样就不是树了，所以不行
这样我们就得到了所有平台的 \(\sum h\) 是 \(O(n)\) 的，所以 \(h\) 的不同个数只有 \(O(\sqrt n)\) 种，对于每一种暴力做即可

时间复杂度 \(O(n\sqrt n)\)

#include <bits/stdc++.h>
#define F(i,x,y) for(int i=(x);i<=(y);i++)
#define DF(i,x,y) for(int i=(x);i>=(y);i--)
#define ms(x,y) memset(x,y,sizeof(x))
#define SZ(x) (int)x.size()-1
#define all(x) x.begin(),x.end()
#define pb push_back
using namespace std;
typedef long long LL;
typedef unsigned long long ull;
typedef pair<int,int> pii;
template<typename T> void chkmax(T &x,T y){ x=max(x,y);}
template<typename T> void chkmin(T &x,T y){ x=min(x,y);}
inline int read(){
    int FF=0,RR=1;
    char ch=getchar();
    for(;!isdigit(ch);ch=getchar()) if(ch=='-') RR=-1;
    for(;isdigit(ch);ch=getchar()) FF=(FF<<1)+(FF<<3)+ch-48;
    return FF*RR;
}
const int N=200100,inf=1e9;
int n,h[N],ans[N],d[N];
bool vis[N];
vector<int> adj[N],buc[N],sto[N];
void dfs1(int u,int fa){
    vis[u]=true;
    for(int v:adj[u]) if(h[u]==h[v]&&v!=fa) dfs1(v,u),chkmin(d[u],d[v]+1);
}
void dfs2(int u,int fa,int D){
    chkmin(d[u],D);
    for(int v:adj[u]) if(h[u]==h[v]&&v!=fa) dfs2(v,u,d[u]+1);
}
queue<int> que;
int main(){
    n=read();
    ms(h,-1);
    F(i,1,n){ int x=read();if(x) h[i]=0,que.push(i);}
    F(i,1,n-1){ int x=read(),y=read();adj[x].pb(y),adj[y].pb(x);}
    while(!que.empty()){
        int u=que.front();que.pop();
        for(int v:adj[u]) if(h[v]==-1) h[v]=h[u]+1,que.push(v);
    }
    F(i,1,n){
        sto[h[i]].pb(i);
        bool rest=false;
        for(int j:adj[i]) if(h[i]==h[j]){ rest=true;break;}
        if(rest) buc[h[i]].pb(i);
    }
    F(i,1,n) ans[i]=h[i];
    DF(i,n,0) if(!buc[i].empty()){
        ms(d,0x3f),ms(vis,0);
        for(int st:buc[i]) d[st]=0;
        F(j,i,n){
            for(int x:sto[j]) if(!vis[x]) dfs1(x,-1),dfs2(x,-1,inf);
            for(int x:sto[j]) for(int y:adj[x]) if(j+1==h[y]) chkmin(d[y],max(0,d[x]-1));
        }
        F(j,1,n) if(!d[j]) chkmin(ans[j],i);
    }
    F(i,1,n) printf("%d ",2*h[i]-ans[i]);puts("");
    return 0;
}