<算法笔记01>ST表
st表
-
需求：输入一个序列\(A[n]\)，进行\(q\)次查询，每次查询求\([l,r]\)区间的最大值。
-
问题：暴力的求法是，每次都遍历一下，求最大值，显然这个非常慢。所以我们需要引入一个高效的数据结构。
-
介绍：st表根据倍增思想实现的数据结构，主要用来求解RMQ问题，\(O(1)\)的时间复杂度求出某个区间的最大值，最小值。
算法介绍
预处理
首先，我们设\(STMax[i][j]\)：从\(i\)开始的区间长度为\(2^j\)的最大值，即区间范围为\([i,2^j-1]\)。
那么很显然，对于原数组\(A[]\)，我们有\(A[i]=STMax[i][0]\)。我们直接读入即可。（不用再建立\(A[]\)数组）
for(int i=1;i<=n;i++){
scanf("%d",&st[i][0]);
}
我们如何去维护好\(STMax[i][j]\)呢，很简单，根据\(max\)最大值的一个性质，\(max(1,2,3,4)=max(max(1,2),max(3,4))\)。是不是看到公式就头晕，让我们来举个例子。
假设已知区间\([1,2][3,4]\)的最大值分别为\(a,b\)，我们要求\([1,4]\)的最大值，只需要求\(max(a,b)\)。
好，我们继续深入，如果要求\([1,8]\)的最大值，我们只需要求出\([1,4],[5,8]\)的最大值，然后在他们之中再取最大值即可。一直递增，我们可以求出更多的最大值，这个便是区间动态规划。
所以我们可以维护好区间长度，不断递推出更多的区间长度。（看不懂没关系，看下文分析）
我们上文说到，我们对所有\(STMax[i][0]\)进行赋值，他们的区间长度都是1，最大值都是原数据\(A[i]\)本身。那么我们是不是得到了所有长度为1的区间的最大值？，因此我们可以去求长度为2的区间的最大值。
接下来我来分析前三步。
- 求长度区间为2的最大值
根据\(max(max([1])，max([2]))\)我们可以得到\([1,2]\)这个长度为2的区间的最大值，同样的，我们能得到\([2,3],[3,4][4,5]...[N-1,N]\)所有长度为2的区间的最大值。
- 求长度区间为4的最大值
根据上面举的例子，求出\([1,4],[2,5],[3,6]....\)所有长度区间为4的
- 求长度区间为8的最大值
求出所有长度区间为8，的最大值
...............................................
我们每一步都可以在上一步的基础上得到更大的区间。区间长度不断翻倍增长(不断乘2)，回到我们上面的定义：我们设\(STMax[i][j]\)：从\(i\)开始的区间长度为\(2^j\)的最大值，所以我们在声明数组的大小的时候，第二维的最大值为整个区间的长度的对数。一般我都设置为21（大概\(2^{21}=2e6\)）
- 声明ST表
int STMax[N][21];
- 维护ST表的代码如下
仔细看代码，别看到符号就觉得难。\((1<<j)\)代表的是\(2^j\)
for(int j=1;j<=log(n);j++){//j代表的是区间长度，n代表原数组的长度，区间长度要<=log(n),原因查看j的实际含义。
for(int i=1;i+(1<<j)-1<=n;i++){//右区间不能越界
STMax[i][j]=max(STMax[i][j-1],STMax[i+(1<<(j-1))][j-1]);
}
}
查询
我们预处理完\(STMax[i][j]\)以后，我们就知道了从任意位置\(i\)开始，区间长度为任意一个2的整数幂的一个区间（\([i,i+2^k-1]\)）的最大值。
不妨问问自己，我们建立这样的数据结构有什么意义呢？
假设，我们现在需要求解[1,4]之间的最大值。
我们可以根据我们的\(STMax[i][j]\)直接求得，其结果为\(STMax[1][2]\)。
但是，如果我们需要求解区间长度为6，\([3,8]\)的最大值，我们该如何是好？
我们不能根据我们建立的\(STMax[i][j]\)直接得到答案。因为我们区间的长度只有2的整数次幂，如果从3开始，让\(j=2,STMax[3][2]\)代表的是\([3,6]\)的最大值，如果我们让\(j=3,STMax[3][3]\)代表的是\([3,10]\)的最大值，明显就超出了我们要求的区间。
我们可以根据上文说到的\(max\)可以相互嵌套的性质。
如果我们求出\([3,6][5,8]\)区间的最大值，然后再取最大值不就是\([3,8]\)区间的最大值了吗?
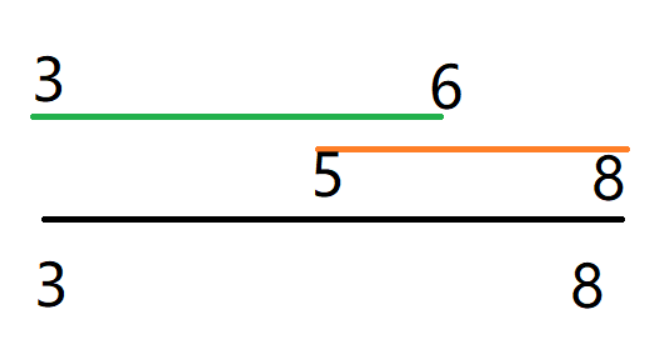
所以我们的策略是这样，对于\([l,r]\)的区间，即次区间长度为\(le=r-l+1\)，我们可以构建两个长度为\(log_2^{le}\)的相交区间。这个值很巧妙，会确保两个区间之并集一定覆盖整个区间，还请读者细细体会。
因此对于一个区间的查询
int query(int l,int r ){
int k=log(r-l+1);
return max(STMax[l][k],STMax[r-(1<<k)+1][k]);
}
我们反复求解\(log(r-l+1)\)也挺浪费时间的，所以我们可以预处理，建立\(log[]\)数组
for(int i=2;i<N;i++){
lg[i]=lg[i/2]+1;
}
算法模板
以洛谷的模板题解完结此篇文章。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+5;
int STMax[N][23];
int lg[N];
int query(int l,int r ){
int k=lg[r-l+1];
return max(STMax[l][k],STMax[r-(1<<k)+1][k]);
}
int main() {
int n,m;
for(int i=2;i<N;i++){
lg[i]=lg[i/2]+1;
}
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
scanf("%d",&STMax[i][0]);
}
for(int j=1;j<=log(n);j++){
for(int i=1;i+(1<<j)-1<=n;i++){
STMax[i][j]=max(STMax[i][j-1],STMax[i+(1<<(j-1))][j-1]);
}
}
while(m--){
int l,r;
scanf("%d%d",&l,&r);
printf("%d\n",query(l,r));
}
}
