<题单>#7题解
写在前面:本题单的思维主要以贪心为主,去训练如何去用结构体排序构造一个最优的策略。部分题不用结构体排序。
前缀知识——结构体排序
STL库的sort想必大家都有用过,经过sort排序之后的int数组,是默认升序的,如果我们想让其变为降序,有没有办法呢? 答案是有的。就是自定义排序规则。降序代码如下
arrary[100];
bool cmp(int a,int b){
return a>b;
}
sort(arrary,arrary+100,cmp);//第三个参数传的是自定义排序规则
sort内部既然会进行排序,就会进行比较,因此改变比较规则就能实现我们想要的排序。
上述代码就是int a,int b,分别代表int数组里面的两个数字,如果a大,就在sort内部返回true,反之就是false,因此经过每一次比较后,整个数组就会自然呈现左边的数字大,有右边的数字小,也就是降序啦。
那么我们如何对结构体进行排序呢?
首先结构体是没有默认的比大小的方式的,比如下列代码。
struct node{
int a;
int b;
}r[100];
node q1,q2;
bool f=q1<q2;//两个结构体进行比较 报错
sort(r,r+100);//报错
肯定会出现报错,因为结构体是没有默认的排序规则的,因此我们对结构体排序的时候,要在sort函数的第三个参数,传入我们自定义的排序规则compare,一般命名为cmp。
接下来 我们对结构体node数组,利用sort函数,进行以a升序的规则进行排序
struct node{
int a;
int b;
}r[100];
bool cmp(node q,node p){
return q.a<p.a;
}
bool cmp(q w, q)
sort(r,r+100,cmp);
这样可以顺利就完成排序了。
勇者斗恶龙
你会获得一个初始攻击力a。在与恶龙作战时,如果你的攻击力大于它的攻击力,你就可以击败这条恶龙并且获得它所提供的攻击力。
解析
首先如果我们全排列去组合所有打龙的顺序,时间复杂度是\(O(n!)\)。
所以我们思考,如何选择一个优秀的策略去打龙呢?
玩过游戏的人都知道,肯定要打经验最高的怪物,所以我们可以对经验值进行降序,对于经验值相同的怪呢?我们肯定先打最好打的怪,每一步选择都是最优的,这就是贪心思维。
所以我们对龙的奖励进行降序,对于奖励相同的龙,攻击力进行升序,不断进行打龙的这个操作,由于我们每一步都是最优的选择(获得的经验是最高的),如果出现所有龙都打不过了,表明我们是打不过这个龙的。
#include<bits/stdc++.h>
using namespace std;
struct el {//恶龙
int x, y;//攻击力 奖励的攻击力
}r[1001];
bool book[1001];//标记数组
bool cmp(el a, el b) {//自定义排序规则
if (a.y== b.y) {
a.x < b.x;//奖励同的情况下,攻击力低的升序
}
else {
return a.y > b.y;//不同的,依据奖励大小降序
}
}
int main() {
//打你能打的范围以内 奖励的攻击力最大的
int a, n;
cin >> a >> n;
for (int i = 0; i < n; i++) {
cin >> r[i].x >> r[i].y;
}
sort(r, r + n, cmp);
int cnt = n;//剩余龙的数目
while(cnt!=0){
int i = 0;
bool flag = 0;//表示本回合是否打龙了
while (i < n) {
if (r[i].x < a) {
a += r[i].y;
flag = 1;
break;
}
i++;
}
if (flag != 1) {//没打龙,表示打不过了。
cout << "NO";
return 0;//return 直接终止程序
}
cnt--;
}
cout << "YES";
return 0;
}
字符串排序
我们先定义两个关于字符串的函数:
1、lower(string s):返回字符串 s 的小写形式,例如lower("AbcD") = "abcd"
2、alpha(string s):返回字符串 s 的字典序
现在给你 n 个字符串,请你对alpha(lower(s))按照从小到大的顺序输出他们,需要注意的是,当alpha(lower(a)) = alpha(lower(b))时,则按照他们出现的先后顺序输出。
前缀知识
- tolower(char x),把x变为小写
- toupper(char x),把x变为大写
- 字典序比较:根据字符串第一个不相同的字符的大小进行比较
- abc>aba
- azb>abz
- baaaa<z
解析
字符串是一个封装好的类,它内部的比较机制就是靠字典序的大小比较,因此两个字符串a,b的字典序比较结果就直接比较即可。
bool res=a<b;
对于lower(string s),我们可以这样,这样s就会变成小写的了
for(int i=0;i<s.length();i++){
s[i]=tolower(s[i]);
}
所以我们这样写就完事了
#include<bits/stdc++.h>
using namespace std;
string r[100005];
string stringLower(string s){//字符串全部变为小写
for (int i = 0; i < s.length(); i++) {
s[i] = tolower(s[i]);
}
return s;
}
bool cmp(string a, string b) {
return stringLower(a) < stringLower(b);
}
int main() {
int n;
cin >> n;
for (int i = 0; i < n; i++) {
cin >> r[i];
}
sort(r, r + n, cmp);
for (int i = 0; i < n; i++) {
cout << r[i] << endl;
}
}
结果当然是超时了,不用多说。
我们来j简单地,粗略地,分析一下时间复杂度
- sort的平均时间\(O(nlogn)\)
- sort内部平均要进行\(O(\frac{logn+n}{2})\)次比较,每次比较都要进行两个字符串转化,字符串最多长度为10,那么最坏时间复杂度就是\(O((logn+n)*10)\),
- 那么时间最最后是\(O(nlogn+10n+10logn)\).... 感觉非常的大了。、
因此,我们要对字符转化进行优化,我们可以一开始就把字符串小写的形式存好,然后排序的时候就用小写的字符串进行排序,最后输出再输出原字符串即可。
#include<bits/stdc++.h>
using namespace std;
struct str {
string a;
string b;
int id;
}r[100005];
string stringLower(string s){//字符串全部变为小写
for (int i = 0; i < s.length(); i++) {
s[i] = tolower(s[i]);
}
return s;
}
bool cmp(str q, str w) {
if (q.a == w.a) {
return q.id < w.id;//越早出的越在前面
}
return q.a < w.a;
}
int main() {
int n;
cin >> n;
for (int i = 0; i < n; i++) {
cin >> r[i].b;
r[i].id=i;
r[i].a=stringLower(r[i].b);
}
sort(r, r + n,cmp);
for (int i = 0; i < n; i++) {
cout << r[i].b << endl;
}
}
积木-3
给你 n 堆积木,第 i 堆积木有 a[i] 个,现在你需要处理以下三种操作:
1 L R x:给区间 [L,R] 内的每堆积木添加 x 个,即对于 L <= i <= R,a[i] += x。
2 L R x:把区间 [L,R] 内的每堆积木拿走 x 个,即对于 L <= i <= R,a[i] -= x。注意,如果拿之前 a[i] 不足 x 个则全部拿完。
3 y:询问第 y 堆积木有多少个,即输出 a[y]。
第一行是一个正整数 n 代表积木的堆数。(1 <= n <= 100000)
然后是 n 个正整数代表每堆积木的个数。(1<= a[i] <= 10000)
第三行是一个正整数 m 代表操作的次数。(1 <= m <= 10000)
接下来 m 行,每行代表一个操作,保证所有的 1 <= L <= R <= n,1 <= x <= 10000,1 <= y <= n。
解析
用暴力铁定超时,我们来分析一下最坏情况下的时间复杂度。
不断地对区间极限做1或2的操作,时间复杂度就是\(O(n*m)\)
- 正解:
因此我们需要改变策略,我们观察题目,我们的输出是可以很快速的通过数组输出,但是主要耗费时间在1和2的操作上面。
因此我们可以把1和2的操作记录下来,每次查询x的时候,的时候调取这些记录的区间,是否x在这些操作的区间之内。
我们分析一下最坏时间复杂度,假设我们查询的操作是x次,并且查询都在最后,都要去遍历之前的所有的操作次数,需要花费\(O(x*(m-x))\)的时间,即\(O(xm-x^2)\),这个最大值取在x=m/2的时候,最后是\(O(\frac{m^2}{4})\),估计一下这个方案勉强可行。
#include<bits/stdc++.h>
using namespace std;
struct make {
int l;
int r;
int num;//表示增加或减少的数字
}arr[10005];
int a[100005];
int cnt = 0;//表示增加和减少的操作数
int main() {
int n,m;
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> a[i];
}
cin >> m;
while (m--) {
int op,x, l, r;
cin >> op;
if (op == 1) {
cin >> l >> r >> x;
arr[cnt++] = { l,r,x };//快速赋值
}
else if (op == 2) {
cin >> l >> r >> x;
arr[cnt++] = { l,r,-x };//快速赋值
}
else {
cin >> x;
int ans = a[x];
for (int i = 0; i < cnt; i++) {
if (arr[i].l <= x && arr[i].r >= x) {//如果在区间之内
ans = max(0, ans + arr[i].num);
}
}
cout << ans << endl;
}
}
}
校门外的树-困难
嘉庚学院大门外长度为L的马路上有一排树,每两棵相邻的树之间的间隔都是1米。我们可以把马路看成一个数轴,马路的一端在数轴0的位置,另一端在L的位置,数轴上的每个整数点(即0,1,2,……,L)都种有一棵树。由于马路上有一些区域要用来建地铁。这些区域用它们在数轴上的起始点和终止点表示。 已知任一区域的起始点和终止点的坐标都是整数,区域之间可能有重合的部分。现在要把这些区域中的树(包括区域端点处的两棵树)移走。你的任务是计算将这些树都移走后,马路上还有多少棵树。
解析
现在剖析一下题目模板,题目可以变为,求多个区间的并集,也就是区间合并。
现在我们看,对于两端区间\([l_1,r_1]\)\([l_2,r_2]\),他们有如下三种情况
-
存在交集
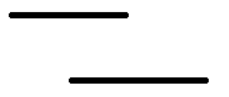
取并集后

-
一个区间被另一个区间包容

取并集后

-
不存在交集
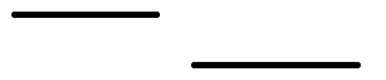
取并集后

因此我们可以对区间进行一个合并操作,但是如果我们不断遍历区间然后合并区间....非常的麻烦,所以我们有一个策略,对每段区间的开始时间进行升序排列。我们从前往后遍历区间的时候,就可以不断维护我们的区间进行合并。所以我们要维护我们上一个大区间的最右边的下标R,不断地和新区间比较,就可以实现我们的区间合并。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
struct tree {
int l, r;
}arr[100001];
bool cmp(tree a, tree b) {
return a.l < b.l;
}
int main() {
ll L, m;
cin >> L >> m;
for (int i = 0; i < m; i++) {
cin >> arr[i].l >> arr[i].r;
}
sort(arr, arr + m, cmp);
ll R = arr[0].r;//上个大区间最右边
for (int i = 1; i < m; i++) {
if (arr[i].r <= R) {//区间被包含 情况3
arr[i].r = arr[i].l - 1;//直接把这个区间作废掉 这步看不懂的话看最后
}
else if (arr[i].l <= R) {//区间存在交集 情况2
arr[i].l = R + 1;
R = arr[i].r;//R变化了 维护R
}
else {//没有相交的部分
R = arr[i].r;
}
}
for (int i = 0; i < m; i++) {
L -= (arr[i].r - arr[i].l + 1);//不断减每个区间的贡献度
}
cout << L+1 << endl;
}
- 另外一种解法,不断维护上一个大区间的L和R
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
struct tree {
int l, r;
}arr[100001];
bool cmp(tree a, tree b) {
return a.l < b.l;
}
int main() {
ll L, m;
cin >> L >> m;
for (int i = 0; i < m; i++) {
cin >> arr[i].l >> arr[i].r;
}
sort(arr, arr + m, cmp);
ll r = arr[0].r;//上个大区间最右边
ll l = arr[0].l;
for (int i = 1; i < m; i++) {
if (arr[i].r <= r) {//区间被包含
arr[i].r = arr[i].l - 1;
}
else if (arr[i].l <= r) {//区间存在交集 1 2 2 2
arr[i].l = r + 1;
r = arr[i].r;//维护R
}
else {//没有相交的部分
//结算区间长度
L -= (r - l + 1);
//维护新的区间
r = arr[i].r;
l = arr[i].l;
}
}
//最后还要结算区间长度
L -= (r - l + 1);
//要注意L+1
cout << L+1 << endl;
}
几何题8-多少全等
给你 n 个三角形,问你能在这些三角形中,最多找出多少个全等三角形
解析
全等三角形的特性SSS,所以我们可以对每一条边长度进行从大到小存储,然后放进结构体排序,就可以迅速的找到全等的三角形。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
struct node {
int a, b, c;
}arr[100001];
bool cmp(node q, node p) {
if (q.a == p.a) {
if (q.b == p.b) {
return q.c < p.c;
}
return q.b < p.b;
}
return q.a < p.a;
}
bool judge(node q, node p) {
if (q.a == p.a && q.b == p.b && q.c == p.c)
return true;
return false;
}
int main() {
int n;
cin >> n;
for (int i = 0; i < n; i++) {
int x1, x2, x3, y1, y2, y3;
cin >> x1 >> y1 >> x2 >> y2 >> x3 >> y3;
int a = (x1 - x2)*(x1 - x2) + (y1 - y2)*(y1 - y2);
int b = (x1 - x3)*(x1 - x3) + (y1 - y3)*(y1 - y3);
int c = (x3 - x2)*(x3 - x2) + (y3 - y2)*(y3 - y2);
if (a < b) {
swap(a, b);
}
if (a < c) {
swap(a, c);
}
if (b < c) {
swap(b, c);
}
arr[i] = { a,b,c };//快速赋值
}
int res = 0;
int cnt = 0;
sort(arr, arr + n,cmp);
for (int i = 1; i < n; i++) {
if (judge(arr[i], arr[i - 1])) {
cnt++;
}
else{
res = max(res, cnt+1);//要多一个
cnt = 0;
}
}
res = max(res, cnt + 1);
if (res == 1) {//没有全等三角形
res = 0;
}
cout << res << endl;
}
LWJ and ARRAY
解析
我们对每个数字进行存储,只需要存储其出现的次数,如果出现的次数最大,就保存其下标
解法一数组存储:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int r[1000005][3];//r[i][0]表示数字出的次数 r[i][1]表示数字最早出现 r[i][2]表示数字最晚出现下标
int main(){
int n;
cin >> n;
int mx = 0;//记录出现最多的数字
int cnt = 0;//记录出现次数最多的次数
for (int i = 1; i <= n; i++) {
int x;
cin >> x;
if (r[x][0] == 0) {
r[x][1] = i;
}
r[x][2] = i;
r[x][0]++;
if (r[x][0] > cnt) {
cnt = r[x][0];
mx = x;
}
}
cout << r[mx][1] << " " << r[mx][2] << endl;
}
解法二 map+pair
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
map<int, pair<int,pair<int, int>>>mp;
int main(){
int n;
cin >> n;
int mx = 0;//记录出现最多的数字
int cnt = 0;//记录出现次数最多的次数
for (int i = 1; i <= n; i++) {
int x;
cin >> x;
if (mp[x].first==0) {
mp[x].second.first = i;
}
mp[x].second.second = i;
mp[x].first++;
if (mp[x].first > cnt) {
cnt = mp[x].first;
mx = x;
}
}
cout << mp[mx].second.first << " " << mp[mx].second.second << endl;
}
解法一的时间要更快一些,解法二的空间要更少一些,大家自行选择。
成绩排序
有一打试卷,总共 n 份,每张试卷上都有一个学号和成绩,现在请你把这 n 个人的成绩进行一个排序,然后输出他们的名次。
解析
难点就在于,我们弄完名次以后还需要按顺序输出他们的名次,我们可以用两次排序或者数组记录。
解法一:
#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
struct student {
ll id, score;
int m;//名
}r[5005];
bool cmp1(student a, student b) {
return a.score > b.score;
}
bool cmp2(student a, student b) {
return a.id < b.id;
}
int main() {
//两次排序 第一次为了排名次, 第二次为了根据学号输出
int n;
cin >> n;
for (int i = 0; i < n; i++) {
cin >> r[i].id >> r[i].score;
}
sort(r, r + n, cmp1);
int cnt = 2;
r[0].m = 1;
for (int i = 1; i < n; i++) {
if (r[i].score == r[i - 1].score) {
r[i].m = r[i - 1].m;
}
else {
r[i].m = i + 1;
}
}
sort(r, r + n, cmp2);
for (int i = 0; i < n; i++) {
cout << r[i].m << endl;
}
}
解法二:
#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
struct student {
ll id, score;
}r[5005];
int res[5005];//记录名次
bool cmp1(student a, student b) {
return a.score > b.score;
}
int main() {
int n;
cin >> n;
for (int i = 0; i < n; i++) {
cin >> r[i].id >> r[i].score;
}
sort(r, r + n, cmp1);
int cnt = 2;
res[r[0].id] = 1;
for (int i = 1; i < n; i++) {
if (r[i].score == r[i - 1].score) {
res[r[i].id] = res[r[i - 1].id];
}
else {
res[r[i].id] = i + 1;
}
}
for (int i = 1; i <= n; i++) {
cout << res[i] << endl;
}
}
班长请客
假设班上有n名同学,网上有m家店铺可以提供送餐服务。每家店铺由于规模大小不同,最多可提供的套餐数量也有所不同,分别为a1、a2、...、am份。每家店铺为套餐定的单价也有所不同,有的店铺卖得贵,有的店铺卖得便宜,分别为每份c1、c2、...、cm元。班长可以任意地从其中的某些店铺点任意份套餐(但在某家店铺点的套餐数量,不能超过该家店铺最多可提供的套餐数量)。每家店铺在提供送餐服务时,除了按份数和单价的乘积收取套餐费用外,还要收取一笔送餐费用t(固定值,不管送多少份都一样,但是如果从多家店铺订餐,则需要收取多笔送餐费)。
解析一(深度优先搜索
-
由于配送费的存在,我们要尽可能在尽量少的商家购买,因此对于每个商家,策略是把商品买断或是买到我们人数足够为止。
-
观察数据量,只有10个商家,每种商家就两种可能——买或不买,因此我们可以用O(n!)的深度优先搜索,全排列出我们购买商家的可能,如果最后这些商家可以使得我们的人数为0,对答案取一个min。
#include<bits/stdc++.h> using namespace std; typedef long long ll; struct node { int a, c;//a 是商品数 c 是价格 }; node r[15]; bool book[15]; int n, m, t; ll res; void dfs(int left, ll sum) {//剩余学生人数 总花费 if (left == 0) { res = min(res, sum); return; } for (int i =0; i < m; i++) { ll j = min(r[i].a, left);//要么买断,要么买够 if (book[i] == 0) { book[i] = 1; dfs(left - j, sum + r[i].c * j + t); book[i] = 0;//回溯 } } } int main() { int T; cin >> T; while (T--) { cin >> n >> m; res = LLONG_MAX; for (int i = 0; i < m; i++) { cin >> r[i].a; } for (int i = 0; i < m; i++) { cin >> r[i].c; } cin >> t; dfs(n, 0); cout << res << endl; } }
- 优化:可以观察到,对于我们要购买的商家是有存在顺序问题的,假设我们排列出要购买的商家为,a,b商家。如果b商家最贵,我们对于b先进行买断操作,然后对a买够剩余的学生数为止,就会出现并不是最优的情况,因此我们要优先对便宜的商家进行购买,
- 思路:对整个结构体数组进行排序,然后在dfs里面维护一个start参数,从而保证每次都从小买到大。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
struct node {
int a, c;
};
node r[15];
int n, m;
ll res;
int t;
bool cmp(node q, node p) {
return q.c < p.c;
}
void dfs(int left, int start, ll sum) {//深度 剩余学生数 开始数 总和
if (left == 0) {
//如果人数剩余为0了
res = min(res, sum);
return;//一定要退出
}
for (int i = start; i < m; i++) {//学生的人数
ll x = min(r[i].a, left);
dfs(left - x, i + 1, sum + x * r[i].c + t);
}
}
int main() {
int T;
cin >> T;
while (T--) {
cin >> n >> m;
res = LLONG_MAX;
for (int i = 0; i < m; i++) {
cin >> r[i].a;
}
for (int i = 0; i < m; i++) {
cin >> r[i].c;
}
sort(r, r + m, cmp);
cin >> t;
dfs(n, 0, 0);
cout << res << endl;
}
}
解析二(二进制枚举
- 我们观察到,对于每个商家只有两种可能,买或者是不买,而且我们对其排序优化以后,购买顺序是固定的,所以我们能用二进制枚举出所有的可能。
- 二进制枚举:如果有10个商家,1代表我们在这个商家进行买断或买够的操作。假设二进制串\(1010100000\)代表我们在1,3,5商家里进行购买
- 范围:从\(0000000000\)到\(1111111111 ((1<<10)-1)\)
基础知识
对二进制串的操作:
对于十进制下的341,二进制下的101010101,如果我们想知道其末尾是否是1,很简单对其取&1即可,但如果我们想知道如何去求出这个二进制1的个数,我们可以不断让这个数字右移,直到这个数字为0。
int a=341;
int cnt=0;
while(a!=0){
if(a&1==1){
cnt++
}
a>>=1;
}
cout<<cnt;//1的个数
-
看来你已经完全懂了,那么练习一下:练习一下吐泡泡
-
本题代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
struct node {
int a, c;
};
node r[15];
int n, m, t;
ll res;
bool cmp(node q, node p) {
return q.c < p.c;
}
int main() {
int T;
cin >> T;
while (T--) {
cin >> n >> m;
res = LLONG_MAX;
for (int i = 0; i < n; i++) {
cin >> r[i].a;
}
for (int i = 0; i < m; i++) {
cin >> r[i].c;
}
cin >> t;
sort(r, r + m, cmp);
for (int i = 1; i < (1 <<m); i++) {
int x = i;//代表这种枚举可能的二进制串
int cnt = 0;//第几个商家
ll sum = 0;//花钱总额
int left = n;//学生人数
while (x!=0) {//不断取末尾
if (x & 1 == 1) {
int numb=min(r[cnt].a, left);//本次购买数量 要么买够,要么买断 取最小
sum += numb * r[cnt].c + t;
left -= numb;
}
if (left == 0)break;//人数够了 就不必要枚举这种可能了。
cnt++;//下一个商家
x >>= 1;//右移
}
if (left == 0) {//如果人数够 就和答案比较
res = min(res, sum);
}
}
cout << res << endl;
}
}
喵星人的共享汽车
在喵星球上,日期的记录方法比较简单,就是从喵王国诞生开始起,记作第1天、第2天、...、第t天、第t+1天、...。有m个喵星人都有自己的租车出行计划,而租车公司只有一辆共享汽车。假定每个喵星人都需要开到很远的地方,以至于还车时,车辆需要有b天的保养时间
解析
- 我们在读取区间长度的时候,对末尾区间长度+一个b 即可。
- 我们对每段区间的末尾进行排序,判断区间之间是否有重合的部分即可。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
struct node {
int l, r;
}arr[10001];
bool cmp(node a, node b) {
return a.r < b.r;
}
int main() {
int T;
cin >> T;
while (T--) {
int m, b;
cin >> m >> b;
for (int i = 0; i < m; i++) {
int l, r;
cin >> l >> r;
arr[i]= { l,r + b };//结构体快速赋值
}
sort(arr, arr + m, cmp);
int R = arr[0].r;
bool flag = 1;
for (int i = 1; i < m; i++) {
if (arr[i].l < R) {
flag = 0;
break;
}
R = arr[i].r;
}
if (flag) {
cout << "Yes";
}
else {
cout << "No";
}
cout << endl;
}
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号