<题单>#1题解
前言
题目链接：http://www.xujcoj.org/Home/Contest/cs/cid/758/ctype/1
第一次写题解，如有错误的地方可以在下面留言，不吝赐教。
一、加法-2
题意
给你两个整数 a 和 b，输出 ( a + b ) % mod 的结果。其中(long long min <= a、b <= long long max，2 <= mod <= long long max)
题解
由于a b mod都非常的大 所以直接运算会爆long long。所以讨论不同情况。
由取模运算的性质可以得到(a+b)%mod=((a%mod)+(b%mod))%mod
-
a<0 && b<0
直接输出0即可 -
a或b 其中一个<=0
根据a b的取值范围可知 两者相加a+b<=long long max -
a>0 && b>0的情况
这种情况有可能会爆long long 所以要进行讨论3.1
a % mod + b % mod <= long long max的时候不会爆long long
这里有一个小细节 如果直接相加 a%mod+b%mod然后再和long long max比较这是有可能会爆 所以我们得简单的处理一下
上面公式等价于a % mod <= mod- b % mod,这样判断比较安全3.2 反之
a % mod + b % mod > long long max(条件一)
这种情况会爆。
先上结论：(a+b)%mod = a%mod - mod + b%mod这样就不会超了推导过程
当mod< a % mod +b % mod < 2mod时 (等式一)
(a+b)%mod 等价于 a%mod - mod + b%mod
为什么呢？ 很简单 (a+b)/mod=1……(a+b-mod)那么我们如何证明等式一成立？
证明如下：
①a%mod<mod
②b%mod<mod
因此①+②<2*mod 再由条件一和题意可得
mod < long long max < a%mod+b%mod
等式一得证
解析二
涂涂：
二、阶乘问题-2
题意
给你一个正整数n，输出 n 的阶乘对 944106571 取模后的结果。
题解
1.n >= mod的时候结果是0。n!=1*2*3*mod*....*n=mod*(1*2*……*n） 那么 n!%mod==0
2.根据数据量，硬算会超时，这个数非质数，所以判断是否在过程中是否出现结果为0的情况。
三、快乐位运算
题意
已知两个正整数 A 和 B，你需要找到一个非负整数 C 使得 (A | C) ^ (B & C) 的值尽可能小，由于这样的 C 可能会有很多，所以你只要输出满足要求的最小的 C 就可以
解析
L^R 众所周知^的运算规律 随着L与R的二进制每一位相同的数字越多,结果越小。
观察原式(A | C) ^ (B & C)
左边的或运算只能增加A二进制的1的个数
右边的与运算只能减少B二进制的1的个数
假设：所以左边和右边要尽可能的相同所以C=A&B的时候 左右等式相同位数最多
验证:
A=1 B=0
A=1 B=1
A=0 B=0
A=0 B=1
代入验证即可得证
四、快乐位运算-2
题意
罗少在做位运算的时候发现了这样一种现象：两个正整数 a、b 在某些情况下满足 a | b = a ^ b
现在罗少想问问大家，在 1 ~ n 之间存在多少个 x 满足 x | n = x ^ n
题解
①1|0=1^0
②0|0=0^0
判断一下a的二进制0的个数,组合一下就好了，但是要注意b的不能全为0。
五、快乐位运算-3
题意
把一个无符号整数的二进制形式的前16位和后16位交换，形成一个新的无符号整数，输出该数。
题解
位运算+或运算
六、异或运算
题解
？？？？？？？？？？？？
七、异或运算-2
题意
给你 n 个数字，你需要删除其中一个数使得剩下的 n - 1 个数字的异或值最大。
题解
数据量1e5,不要想着用冒泡排序啦。
利用异或运算的特性
0和任意一个数字取亦或就是其本身
自身和自身亦或运算为0
定义一个记录总和变量sum=0 然后去异或每一个数字（意义上和累加同理）
再用sum对每个数字分别取亦或取一个最大值即可。
八、异或运算-3
题解
??
九、高次幂运算
题解
涂涂：？？？？？？
十、高次幂运算-2
题意
p = (b ^ c) % d，
q = (a ^ p) % d。
其中 ^ 为次方运算。
四个正整数a、b、c、d。(1 <= a、b、c、d <= 1e18)
题解
a,b,c,d太大会爆long long，要利用慢速乘
在快速幂的取模时，利用慢速乘来代替乘法，可以防止避免爆long long
十一、高次幂运算-3
题意
计算 a 的 b 次方对 1e9+7 取模以后的结果。(1 <= a，b <= 1e100)
题解
a、b字符取模处理，快速幂处理（新生先不写）
十二、数列求和
题意
现在有一个数列：1、4、9、16、25、36…
求这个数列的前n项和%1000000007的结果
解析
利用费马小定理推论式:mod为素数时，(a/b)%mod=a*(b)^(mod-2)%mod
小学二年级就知道的自然数平方级数的求和通项公式为
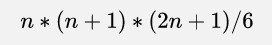
由于mod为质素，所以我们利用上述公式得到
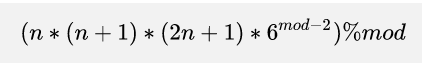
再根据取模运算性质得到
(错误公式 思考一下为什么~)
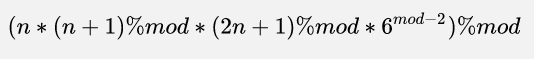
(正确公式)
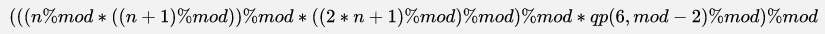
Ps: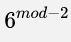
这一块利用快速幂取模~
十三、数列求和-2
题意
现在有一个数列：1、3、6、10、15、21…
求这个数列的前n项和%mod的结果。(1 <= n <= 1e9，1<= mod <= 1e9+7)
题解
利用自然数平方和通项公式加等比数列可推出
对其取模
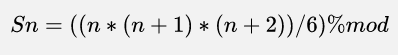
但是
1、分数不能取模
2、mod不一定是质数(无法费马小推论式求逆元）
我们仔细观察，发现n和mod数都不太大（相乘不会爆long long ）。
所以可以用以下公式(重点来了
直接乘法取模就可以了
十四、数列求和-3
题意
现有一个首项为 q ，公比为 q ，项数为 n 的等比数列，求这个数列的和对 mod 取模后的结果。q、n、mod。(1 <= q、n、mod <= 1e9)
题解
通项公式:
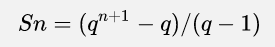
取模:
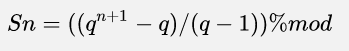
需要用到13题的那个公式，再用到第10题的慢速乘，结果就出来啦！！！
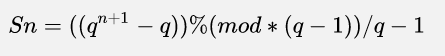
一定要慢速乘，因为模数很大，如上述公式，处理后的模数是mod*(q-1)。
这里还有一个坑，注意看题目的取值范围。
十五、专业代表-2
题意
有一场讲座需要每个专业派出一名代表去参加。现假设有n个专业，第i个专业有ai个人，请问出席这场讲座的代表总共有多少种可能的组合？由于答案可能很大，所以你只需要输出它对p取模后的结果。
题解
慢速乘板子题，直接累乘即可。
十六、专业代表-3
题意
有一项活动需要每个专业派出一些代表去参加，已知现在有n个专业，第i个专业有ai个人，并且每个专业都需要从这ai个人中派出bi个人去参加活动。请问参加这场活动的人有多少种可能的组合。
由于结果可能很大，所以你只需要输出它对1e9+7取模之后的结果，然后换行。(1 <= n <= 1e5) (1 <= ai <= 20000) (1 <= bi <= ai)
题解
根据题意和高中数学知识
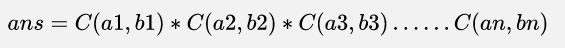
所以对其取模
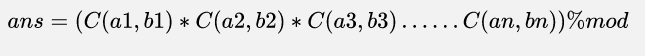
根据我们的知识就知道
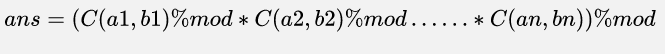
对于第i项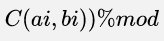
其展开式为 fac[i]=i!
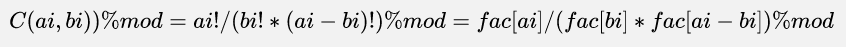
这里有个技巧，如果每次运算都去求fac[i]%mod 非常的浪费时间，因此我们可以用一个非常扎实的技巧————打表
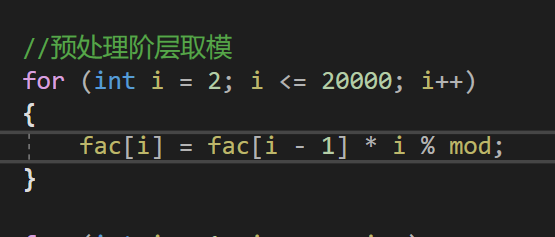
这样每次我们调用fac[i]的时候就能很快地得到阶乘
其次，对于上述公式的除法取模，直接费马小推论式即可，前几题都有类似的方法，在这不多赘述了。
十七、探险小队
题意
有n个人报名参加了探险小队，你作为这个探险小队的负责人，需要从中选取至少1人至多n人去参加任务，并从选取的人中任命一个队长。
题解
从n个人里选i(1n)个，i个人每个人都可以当队长就是i种情况，所以一共是C(n,i)*i，从i=1n累加一下就好了
公式为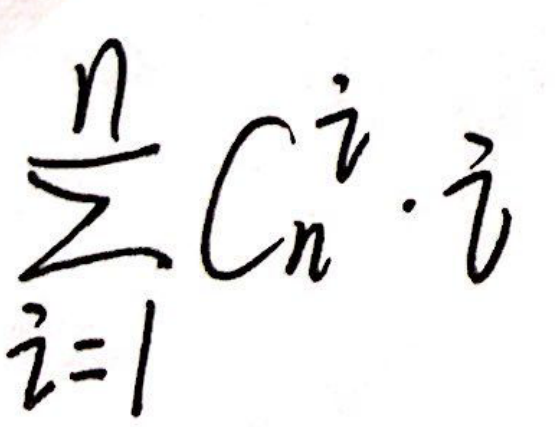
简单的推导后通项公式为：
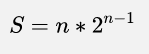
公式都给你了 快速幂闭眼做好吧！！！
推导过程：
推导方式一：
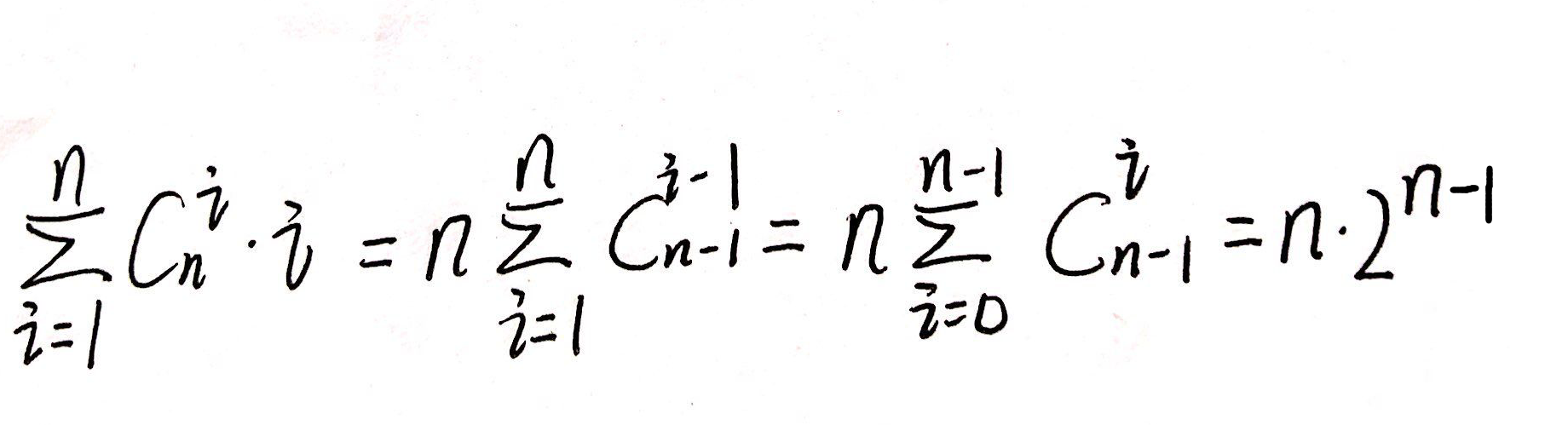
推导方式二：
十八、探险小队-2
十九、探险小队-3
题意
探险者们在外出活动时需要选择两名队员在营地看守，现在总共有 n 名探险者，每个人都有一个能力值，由于某种关系，在营地看守的那两名探险者能力不能相差太多，具体地说，能力较高的探险者的能力值不能超过能力较低的探险者的能力值的两倍，请你帮他们算一下，总共有多少种选择的可能。
对于 100% 的数据，n <= 100000。x <= 1e9。
题解
数据量不大，可以考虑用排序+二分查找，用sort排个序，然后遍历数组，对于a[i],二分查找大于2*a[i]的数字的位置k，然后不断去累加(k-i)之间数字个数就好了。
二十、数列
题意
有一个数列，a[1] = 1，a[2] = 2，当 n >= 3 时：a[n] = 4 * a[n - 1] - 3 * a[n - 2]，你的任务是计算这个数列的第 x 项。x <= 1e10。
题解
由于x太大，不可能用循环遍历去迭代了。所以还是推导一下公式
通项公式：
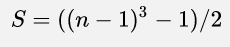
看数据量，快速幂+慢速乘
推导过程
