OI集训 Day27

Content：网络流
Date：2025.8.12

课堂内容

二分图匹配

Hall 定理

假设 \(G = (X,Y,E)\) 是一个二分图，且 \(|X| \le |Y|\)。对于 \(W \subseteq X\)，记 \(N_{G}(W)\) 表示在图 \(G\) 中所有与集合 \(W\) 中的点相邻的点的集合。那么 \(X\) 的完美匹配存在，当且仅当 \(|W| \le |N_G(W)|\) 对于所有 \(W \subseteq X\) 存在。

匈牙利算法

不断搜索增广路，每次考虑一条增广路，看看把一个匹配拆了能否增加一个新的匹配。

模板代码：Link

网络最大流算法

Dinic

Dinic 是求解网络最大流的其中一个算法，也是最常用的算法。其核心思想为：每次用 BFS 寻找增广路，然后用 DFS 统计增广路上的最大流量。但是这样会有一些问题，如果给定的网络是如下情况的话：

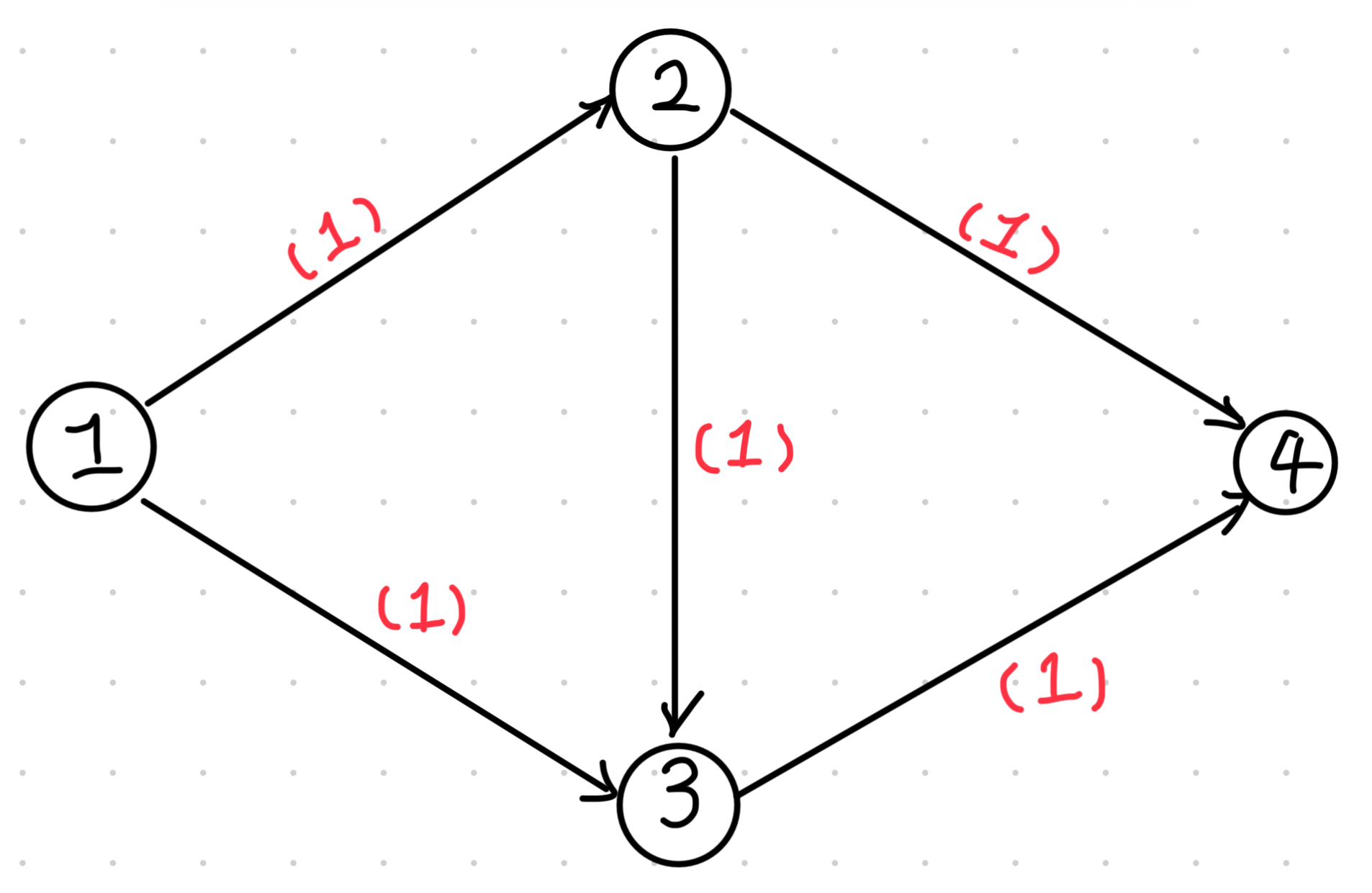
如果直接按照上面说的方法走，第一次增广路可能是 \(1 \to 2 \to 3 \to 4\)，但实际上最优的是 \(1 \to 2 \to 4\) 和 \(1 \to 3 \to 4\)。所以为了解决这个问题，我们需要对原图的所有边建立反向边 \((v,u,0)\)。如果我们选择了这条路，则将其反向边的流量减去我们现在流过这条边的流量，这样可以做到类似反悔贪心的效果。

模版代码：Link

费用流

最小费用最大流 (Min Cost Max Flow, MCMF)

和原来的网络图相比，每一条边新加了一个限制 \(c\) 表示流过 \(1\) 个单位的流量需要花费 \(c\) 的代价。

我们在原来的 Dinic 算法的基础上进行修改，每次沿着最短路径进行增广。由于有带负权的反向边存在，我们不能使用 Dijkstra，而是要使用 SPFA。

模板代码：Link

题目

Luogu-P3254 圆桌问题

题目描述

一共有 \(m\) 个不同国家的代表团来参加国际会议，第 \(i\) 个代表团共有 \(r_i\) 个代表参加会议，会议场地内共有 \(n\) 张桌子，每张桌子最多可以做 \(c_{i}\) 个人。规定一张桌子上不能坐超过一个相同代表团的人。问是否存在一种合法的分配方案。

解题思路

因为一张桌子最多可以做一个同一个代表团的代表，所以我们将每个代表团向每个桌子建一条流量为 1 的边。然后我们把超级源点和每个代表团之间链接一条流量为 \(r_{i}\) 的边，再把所有桌子和超级汇点连接一条流量为 \(c_{i}\) 的边，然后跑最大流即可。

提交记录：Link

模拟题-6.1 子集和

题目大意

给定一个和为 \(m\) 的数组 \(a\)，现在给出一个数组 \(b\)，其中 \(b_{i}\) 表示 \(a\) 的所有 \(2^{n} - 1\) 种不同子集的和中等于 \(i\) 的个数。请根据数组 \(b\) 还原数组 \(a\)。

解题思路

显然，\(b\) 中下标大于 0 第一个非零的位置就是 \(a\) 数组中存在的元素之一。我们考虑重复这个操作得到数组 \(a\)。这里就要考虑这个数 \(x\) 对数组 \(b\) 的影响。其实 \(\displaystyle b_{i} = \sum_{j=1}^{n} b_{i-a_{j}}\)，所以消除 \(x\) 的影响即为：\(\forall i \ge x, b_{i} - b_{i-x} \to b_{i}\)。

具体实现时要注意，由于对于 \(\forall i < x, b_{i-x}\) 不存在，所以直接置为 0 即可，但是对于 \(i=0\) 而言，由于其对 \(b_{x}\) 有贡献，所以要将 \(b_{0}\) 置为 1。然后按照上面对的操作重复下去，直到得出数组 \(a\) 即可。

Code

#include <bits/stdc++.h>

using namespace std;

constexpr int N = 55, M = 10005;
int b[2][M], n, m;

int main() {
    std::ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    
    cin >> n >> m;
    
    for (int i = 0; i <= m; i++) {
        cin >> b[0][i];
    }
    
    int i = 0, t = 0;
    while (i < n) {
        int j = 1;
        while (j <= m && b[t][j] == 0) j++;
        
        for (int k = 1; k < j; k++) b[t][k] = 0;
        b[t][0] = 1;
        
        for (int k = j; k <= m; k++) b[t][k] -= b[t][k - j];
        
        i++;
        cout << j;
        if (i != n) cout << ' ';
    }
    
    return 0;
}