OI集训 Day18

Content：构造
Date：2025.8.3

课堂内容

完全图匹配构造

描述

对于一个 \(n\) （\(n \mid 2\)） 个顶点的完全图，将其分为 \(n-1\) 个匹配。

思路

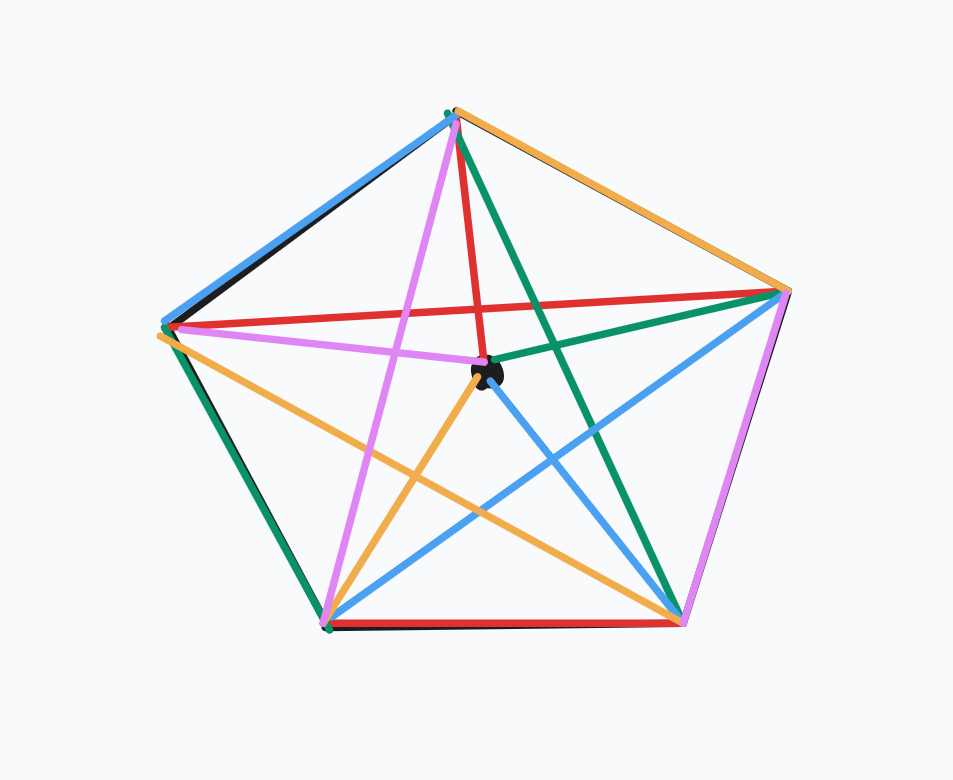
我们将其中一个点提出来，剩下的 \(n-1\) 个点形成一个正多边形，然后将提出的那个点放在中心。

对于每一条 “斜率” 相同的边，我们把他们放在一个方案中，然后对这个方案进行旋转，就构造了 \(n-1\) 个匹配。

完全图曼哈顿路构造

描述

对于一个包含 \(n\) 个点的完全图，要求将其分成 \(\lfloor n / 2 \rfloor\) 条曼哈顿路。

思路

1. 当 \(n \mid 2\) 时
   我们将这些点排成一个正 \(n\) 边形，然后做如下构造：
   
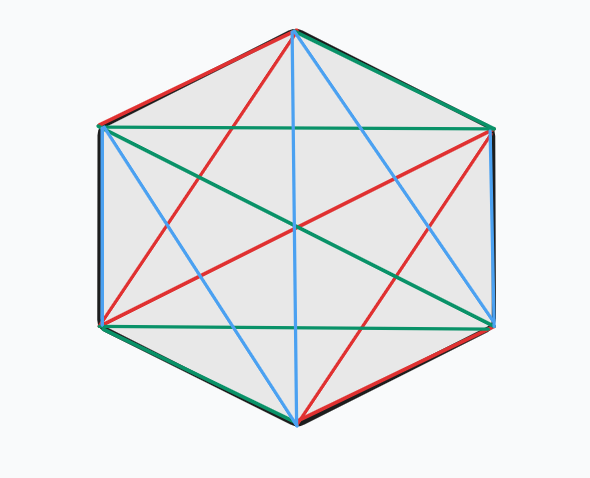
   还是通过第一个构造方案的旋转得出其他的方案。

2. 当 \(n \nmid 2\) 时
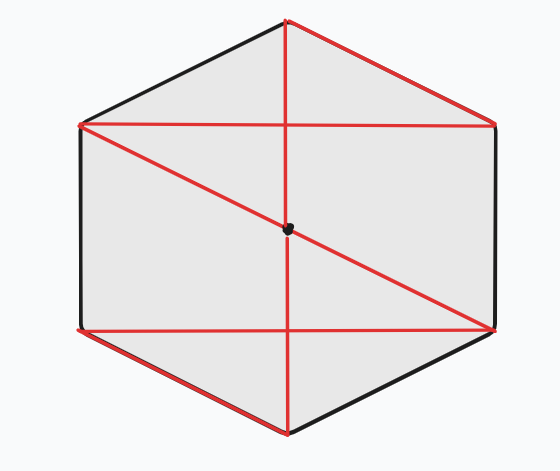
   我们考虑通过上面的构造延伸，构造一个 正 \((n-1)\) 边形，然后在中间加入一个点，把每一条曼哈顿路的起点和中点和这个点相连，就得到了 \(n\) 为奇数时的构造。下面是其中一条曼哈顿回路。
   

后记

今天晚上听了演唱会，所以别问我为什么现在才写。不过演唱会还挺好听的。