并查集原理实现及例题
一.引例
一个班上,同学A和同学B在同一个月出生,同学B和同学C在同一个月出生,同学D和同学E同一个月出生,同学F和同学C在同一个月出生......
问:(1)最多几个人同一个月出生?
(2)任选两个人,他们是否同一个月出生?
要回答这些问题,我们很容易想到,我们只需要把同学都写出来,同一个月份出生的同学相互连接起来,就能很容易得出这个问题的答案。虽然,手写出来耗时耗力气,但是我们有电脑啊!我们所需要做的就是编写代码来完成手动连接的任务,而这个就是所谓的并查集,并查集就是一种用来处理多个不相交集合的合并及查询问题的数据结构。
二.算法原理
我们使用树来表示并查集,我们的操作基于一个int parent[]数组来实现,其中,parent[i]表示i节点的父节点,也就是说parent[i]和i之间是具有相互连通的关系,当我们需要了解两个节点之间是否就有连通性的时候,我们只需要判断两个节点的父节点是否相同即可。
三.初始化init()
一开始所有的点都是独立存在的,相互之间没有联系。

故,我们约定一开始所有的parent[i]均设为-1(为了便于后面合并并查集时比较大小的操作)
四.查询find()
我们先给出一棵树,如下图所示:
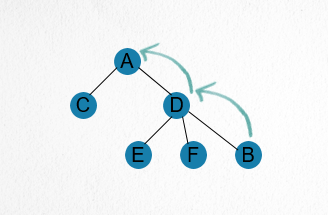
我们查找B的父节点,我们令s = parent[B],之后反复令s = parent[s],直至parent[s]为负数为止(即已经找到根节点)
下面给出find函数的实现:
int find(int x){
int s;
for(s = x; parent[s]>=0; s = parent[s]);
}
但是,这样会出现一个问题,就是如果处理不当,会产生一个退化的树,样子就是一字长龙,如果我们查询最下面的节点,那么我们要逐步往上攀爬直到根节点,复杂度将高达O(N),所以,为了避免这种情况的发生,我们应该要在find的过程中,边进行路径的压缩。
一字长龙:
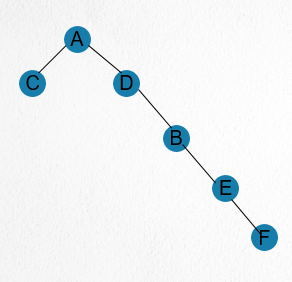
路径压缩:

下面给出完善后的find函数:
int find(int x)
{
int s;
for (s = x; parent[s] >= 0; s = parent[s]);
int tmp;
while (s != x)
{
tmp = parent[x];
parent[x] = s;
x = tmp;
}
return s;
}
五.合并union
为什么要合并呢?因为一开始的时候,所有节点都是独立的,我们需要逐步将节点连接成树。比如我们输入两个节点,这两个节点属于不同的集合,这个时候我们就需要把集合合并,合并的原则是,小集合合并到大集合里面去。即,将小集合的根节点,连接到大集合的根节点上,使得小集合的根节点的父节点为大集合的根节点。那么,如何判断哪个集合更大呢?还记得之前我们约定的所有parent[i]都设为-1,我们在合并的时候,直接比较根节点i的parent[i]大小,大的说明所含元素少,合并时主要要将两个集合的parent[i]相加,即把元素个数加上(用负数表示)。
下面给出实现的union函数:
void union(int R1, int R2)
{
int r1 = find(R1), r2 = find(R2);
if (r1 == r2)
return;
int tmp = parent[r1] + parent[r2];//将根节点数目记录
if (parent[r1] > parent[r2])//如-1和-2比较,-1>-2,故r1所在的集合含有1个元素,小于r2所含的两个元素
{
parent[r1] = r2;//将r1的父节点设为r2
parent[r2] = tmp;//r2的父节点值更新为节点数目(负数)
}
else
{
parent[r2] = r1;
parent[r1] = tmp;
}
}
六.例题,畅通工程
题目链接:https://vjudge.net/problem/HDU-1232
Input:
测试输入包含若干测试用例。每个测试用例的第1行给出两个正整数,分别是城镇数目N ( < 1000 )和道路数目M;随后的M行对应M条道路,每行给出一对正整数,分别是该条道路直接连通的两个城镇的编号。为简单起见,城镇从1到N编号。
注意:两个城市之间可以有多条道路相通,也就是说
3 3
1 2
1 2
2 1
这种输入也是合法的
当N为0时,输入结束,该用例不被处理。
Output:
对每个测试用例,在1行里输出最少还需要建设的道路数目。
这个是一个很典型的并查集的题目,我们可以直接使用板子来答题,我们所需要做的就是,在脑海中建立一个模型,以城镇为节点,以是否有道路相互连接。要找最少还需建设的道路,只需要看还有多少个独立的集合,我们只需要把独立的集合连接起来,那么所有都畅通了。
#include <iostream>
#include <cmath>
#include <cstdio>
#include <cstring>
using namespace std;
int parent[1010] = { 0 }, n, m;
void inint()
{
for (int i1 = 1; i1 <= n; i1++)
parent[i1] = -1;
}
int find(int x)
{
int s;
for (s = x; parent[s] >= 0; s = parent[s]);
int tmp;
while (s != x)
{
tmp = parent[x];
parent[x] = s;
x = tmp;
}
return s;
}
void union1(int R1, int R2)
{
int r1 = find(R1), r2 = find(R2);
if (r1 == r2)
return;
int tmp = parent[r1] + parent[r2];
if (parent[r1] > parent[r2])
{
parent[r1] = r2;
parent[r2] = tmp;
}
else
{
parent[r2] = r1;
parent[r1] = tmp;
}
}
int main()
{
int i, j, count = 0;
while (scanf("%d", &n) != EOF)
{
count = 0;
inint();
if (n == 0)
break;
scanf("%d", &m);
for (int x = 0; x < m; x++)
{
scanf("%d %d", &i, &j);
union1(i, j);
}
for (int x = 1; x <= n; x++)//看还有多少独立的集合
{
if (parent[x] < 0)
{
count++;//若是独立的集合,则count++
}
}
cout << count - 1 << endl;//最后输出count-1为所需的道路数目
}
return 0;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号