《机器学习》第一次作业——第一至三章学习记录和心得
第一章
1、什么是模式识别
-
定义:
根据已有的知识表达,针对待识别模式,判别决策其所述的类别或者预测其对应的回归值。 -
划分:
分为分类与回归两种。分类:输出量为离散的类别表达;回归:输出量为连续的信号表达。
回归是分类的基础,由回归值做判别决策可得到类别值。
如逻辑回归中使用 sigmoid 函数来预测决策概率,其输出是0-1之间的回归值,若再使用 sign 函数,取大于0.5为1,小于0.5为0则得到离散的类别值。 -
应用:
字符、交通标志、动作、语音、应用程序(基于TCP/IP)、银行信贷识别、股票价格预测、目标抓取、无人驾驶...可以说模式识别相较于NLP、CV等是一个范畴更大的概念
2、 模式识别数学表达
-
数学解释:
模式识别可以看作一种函数映射f(x),将待识别模式x从输入空间映射到输出空间。函数f(x)是关于已有知识的表达。
比如猫狗图片分类任务中,一张图片x(3维数组),经过网络f的计算,其结果将是0(猫)或者1(狗) -
模型的概念:
model,关于已有知识的一种表达方式,即函数f(x)
通常记录了函数的权重,如 f=wx+b 里的w。再通常,f会写成矩阵乘积形式,并且w将合并偏置b,即 f=WX -
广义:特征提取+回归器+判别函数
-
狭义:特征提取+回归器
-
分类器:回归器+判别函数
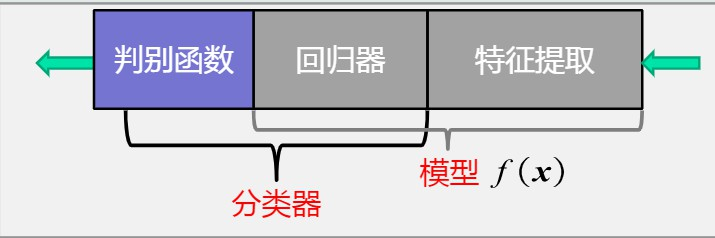
-
判别函数:
特定的非线性函数,记作g。二分类:sign函数;多分类:max函数(取回归值最大的作为结果) -
特征:
用于区分不同类别模式的、可测量的量。
如对于甜橙来说,甜度、颜色、形状、气味、触感...都可以作为特征 -
特征向量:

3、 特征向量的相关性
-
意义:
每个特征向量代表一个模式,计算向量间的相关性,是度量所识别模式是否相似的基础 -
点积:
两个向量 a(a0, a1, ..., an),b(b0, b1, ..., bn) 的点积定义为:a·b = a0b0+a1b1+……+anbn=|a||b|cos<a,b>
使用矩阵乘法并把(纵列)向量当作n×1 矩阵,点积还可以写为:a·b = a.Tb,a.T为矩阵a的转置
点积计算结果为标量,有正有负,数值越大,说明两个向量间越相似 -
投影:
将向量a垂直投射到向量b方向上的长度(标量) a0 = |a|cos<a,b>
在b方向上分解得越多,说明ab方向上越相似当cos<a,b>=0时完全等同
点积ab = 投影a0向量b模长|b| -
残差向量:
向量a分解到向量y方向上得到的投影向量a0与原向量a的误差
ra = a-a0=a-|a|cos<a,b>/|b|b -
欧氏距离:
两个特征向量间的欧式距离可以表征二者之间的相似程度,与投影不同,综合考虑了方向和模长
d(a, b) = sqrt(∑(ai-bi)**2), i=1,2,…,n
4、 机器学习的基本概念
-
线性模型:
模型结构为线性(直线、面、超平面):y=W.T*X
仅适用数据线性可分时,如鸢尾花数据集 -
非线性模型:
模型结构为非线性(曲线、曲面、超曲面):y=g(X)
适合数据线性不可分,如异或问题
常见非线性模型:多项式、神经网络、决策树 -
样本量vs模型参数量:
样本个数与模型参数个数相同:W有唯一解
样本个数大于模型参数个数:W无准确解,往目标函数中额外添加一个标准,通过优化这个标准得到近似解
样本个数小于模型参数个数:W无解/无数个解,还需要在目标函数中加入体现对于参数解的约束条件,据此选出一个最优的解
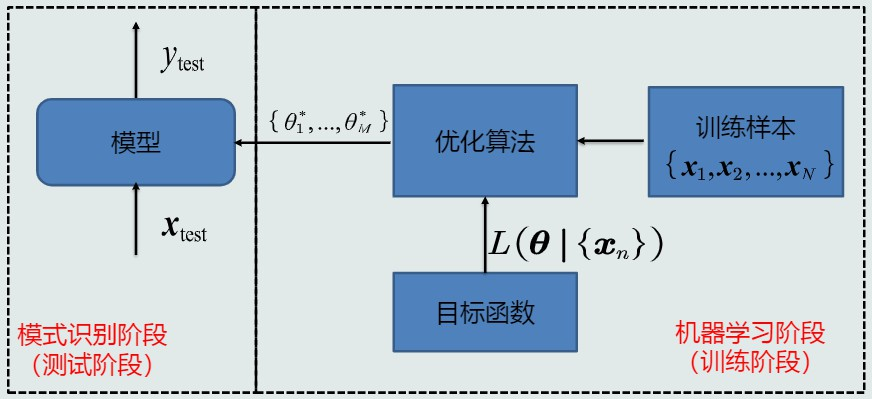
-
监督式学习:
定义:训练样本及其输出真值都给定的学习
即每个样本的正确输出都已知的情况,可以通过最小化模型预测与真值之间的误差来优化模型 -
无监督式学习:
定义:只给定训练样本的学习
难度大于监督式,典型应用为聚类问题、图像分割 -
半监督式学习:
定义:部分训练样本标注,其余未标注的学习
可看作有约束条件的无监督式学习问题:标注过的训练样本用作约束条件,典型应用为网络流数据 -
强化学习:
定义:及其自行探索决策、真值滞后反馈
有些任务需要累积多次决策行动才能知道最终结果。
5、 模型的泛化能力
-
泛化能力
-
定义:训练好的模型不仅能用于训练样本,也要能用于没见过的新样本
泛化能力低:过拟合 -
提高泛化能力
选择复杂模型
往目标函数中添加正则项(如权重的范数|W|,限制模型参数尽量小) -
超参数
如选取的多项式阶数、一组训练样本个数、学习率、正则系数
调参:从训练集划分出验证集,基于验证集调整选择超参数
6、 评估方法与性能指标
-
留出法
随机划分,将数据集分为训练集和测试集,测试集用于评估模型
取统计值,随机进行上述划分若干次,取量化指标平均值作为最终结果 -
k折交叉验证
数据集分为k个子集,取其中一个为训练集,其余作为训练集
重复以不同方式划分k次,使得每个子集都有作为测试集,这k次评估值取平均作为最终结果 -
留一验证
k折交叉验证中k=样本总数n的情况 -
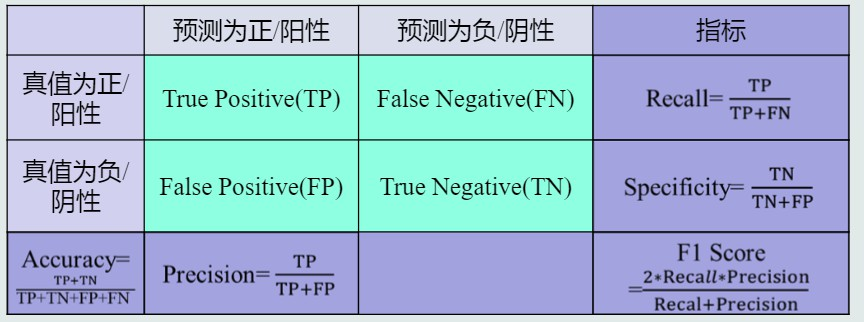
基本概念
真阳性TP、假阳性FP、真阴性TN、假阴性FN
准确度Accuracy,综合阳性与阴性度量识别正确程度,但阳/阴性样本数失衡则难以度量
精度Precision,预测为阳性样本的准确程度,或称查准率
召回率Recall,也作敏感度Sensitivity,全部阳性样本中被预测为阳性的比例,或称查全率
F-Score,通过加权平均综合Precision和Recall,F = (a2 + 1)pr / (a2*p + r)
F1-Score,取F-Score中a=1可得
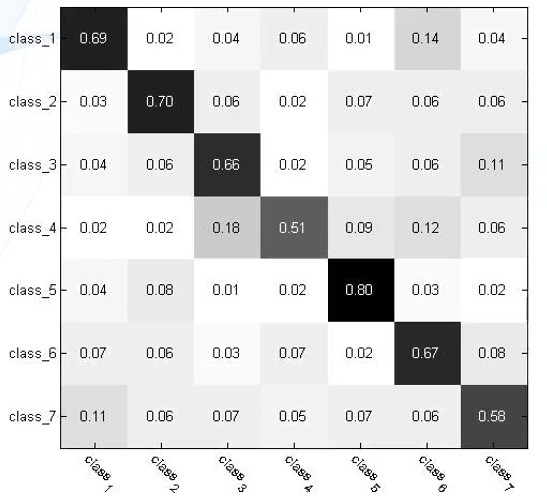
混淆矩阵ConfusionMatrix,总结分类模型预测结果的一个分析表,行代表预测值,列代表真值。每个元素根据每个测试样本预测值与真值的计数统计值得来。对角线值越大,表示模型性能越好。(大概因为对角线处预测值等于真值,元素越大,说明预测正确的情况越多)
- PR曲线
横轴召回率,纵轴精度
精度高且召回率高说明模型性能好,但二者时常矛盾,无法同时很高
理想情况能取到右上角点(1, 1)。曲线越往右上凸,模型性能越好。
第二章
1、 MED分类器
-
类的原型
定义:代表这个类的一个模式或一组量,便于计算该类和测试样本之间的距离
均值作为原型:类中所有训练样本代表误差最小的一种表达方式
最近邻作为原型:表达误差大,对噪声与异常样本敏感 -
距离度量
标准:同一性、非负性、对称性、三角不等式
欧氏距离sqrt(∑(xi-zi)2) = sqrt((X-Z).T * (X-Z))
曼哈顿距离∑|xi-zi| = |X-Z|
加权欧氏距离sqrt(∑wi*(xi-zi)2) = sqrt((X-Z).T * Iw * (X-Z)), Iw为对角元素是wi的对角矩阵 -
概念
采用欧式距离作为距离度量,没有考虑特征变化的不同及特征之间的相关性
计算待分类样本到各个类均值的距离,分类到距离近的类
计算所有类别各自的协方差矩阵,若某cov矩阵对角线元素不相等:该类每维特征的变化不同;非对角元素不为0:该类特征之间存在相关性
2、特征白化
-
目的
通过将原始特征映射到一个新的特征空间,使得在新空间中特征的协方差矩阵为单位矩阵,从而去除特征变化的不同及特征之间的相关性。 -
步骤
解耦,去除特征之间的相关性,即使对角元素为0,矩阵对角化
白化,对特征进行尺度变换,使每维特征的方差相等
解耦转换矩阵W1,白化转换矩阵W2。由W=W2W1
转换后的特征y = Wx
转换后的协方差矩阵∑y = W∑xW.T
求解
对样本x计算其协方差矩阵 ∑x=np.cov(x)
解∑x的特征值与特征向量 λ, ν = np.linalg.eig(∑x)
单位化特征向量 Φ = ν/|v|
所有单位化特征向量组成矩阵 Φ = [...φ...]
所有特征值组成对角矩阵 ∧ = [...λ...] # 实际np.linalg.eig返回的λ就是∧
由Φ∧ = ∑xΦ 得到 ∧ = Φ.T∑xΦ
可见通过Φ将∑x成功对角化,故 W1 = Φ.T
W2 = ∧**(-1/2)
W = W2W1 = ∧**(-1/2) * Φ.T
W1特性:W1转换前后欧氏距离保持一致,故W1只是起到旋转作用
3、MICD分类器
-
最小类内距离分类器,基于马氏距离
马氏距离 sqrt((X-Z).T * ∑i.inv * (X-Z)),∑i.inv为样本i协方差的逆 -
概念
为克服MED缺点:没有考虑特征变化的不同及特征之间的相关性 而提出
采用马氏距离作为距离度量,没有考虑特征变化的不同及特征之间的相关性
计算待分类样本到各个类均值的距离,分类到距离近的类
MICD缺陷:倾向于选择方差大的类
第三章
1、 贝叶斯决策与MAP分类器
引言
MICD倾向于选择方差大的类
像MED、MICD这种基于距离的决策没有考虑类的分布等先验知识
引入概率P(Ci|x),表示样本x属于类别Ci的概率,即后验概率
-
贝叶斯规则
基于先验概率P(Ci)、观测似然概率P(x|Ci)计算后验概率
P(Ci|x) = P(x|Ci)*P(Ci)/P(x),其中P(x)由P(x|Ci)、P(Ci)根据全概率公式可得 -
MAP分类器
最大化后验概率分类器,将测试样本分给后验概率最大的那个类,决策边界是两个后验概率相等的地方。
单维空间通常有两条决策边界,高维空间是复杂的非线性的边界。 -
MAP决策误差
概率误差等于未选择的类所对应的后验概率
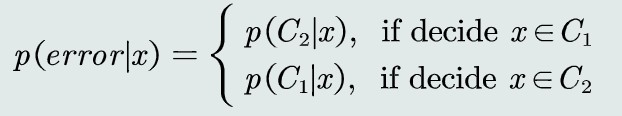
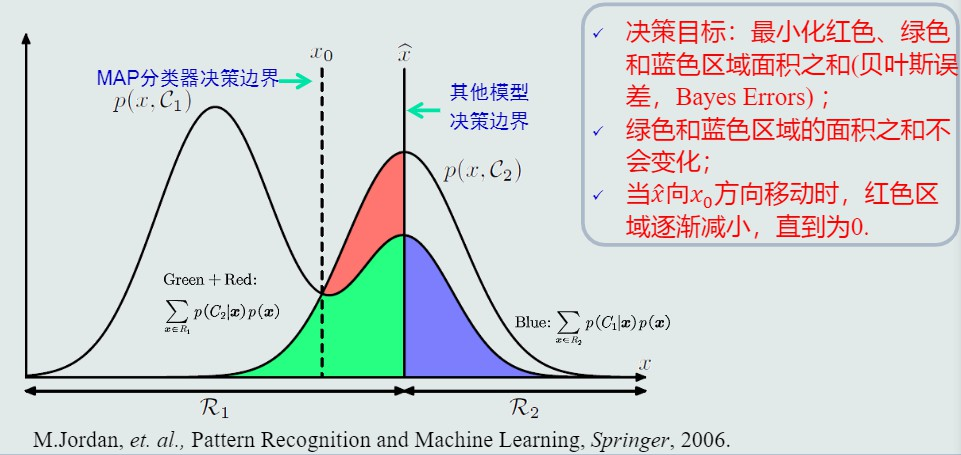
- MAP目标
最小化概率误差,当选用其他模型决策边界为下图中实线,此时若为R1类,则红色与绿色均是误差,若为R2类则蓝色部分是误差。MAP的决策边界下不存在红色区域,故误差最小。
2、 MAP分类器:高斯观测概率
先验和观测概率表达方式
常数表达(P(Ci)=0.2)
参数化解析表达(高斯分布等)
非参数化表达(直方图、核密度、蒙特卡洛等)
观测概率:单维高斯分布
取观测似然概率为一维高斯分布
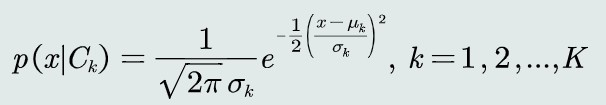
将高斯分布带入MAP分类器,取对数化简MAP的判别公式
若两个类的标准差σ相等,决策边界是线性的,只有一条
当两个类先验概率不同,因为决策边界会偏向(即靠近)先验概率小的类(该类在x轴上区域减小了),即更可能决策为先验概率高的类
若两个类的标准差σ不等,决策边界是非线性的,有两条
此时MAP分类器会倾向于选择方差较小(紧致)的类。
可以看到,MAP倾向于先验概率大、分布集中的类,同时解决了MED与MICD存在的问题。
观测概率:高维高斯分布
取观测似然概率为多维高斯分布
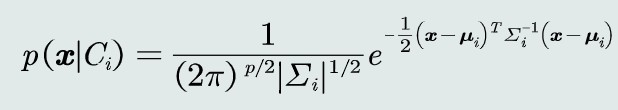
将高维高斯分布带入MAP分类器,取对数化简MAP的判别公式
其决策边界是一个超二次型,始终偏离MICD决策边界一定距离
3、 决策风险与贝叶斯分类器
-
决策风险
贝叶斯决策错误会带来风险,不同的错误决策风险程度也不一致
可定义损失表征当前决策动作相对于其他候选类别的风险程度 -
损失:λ(αi|Cj),简写为λij,其中αi为决策动作,Cj是αi对应的决策类别
λ可以手动设置也可以通过学习训练而来
决策风险R(αi|x) = ∑λij*P(Cj|x) -
贝叶斯分类器
在MAP分类器基础上,加入决策风险因素,就得到贝叶斯分类器
给定一个测试样本x,贝叶斯分类器选择决策风险最小的类 -
贝叶斯决策的期望损失
给定单个测试样本,贝叶斯决策的损失就是决策风险R
对于所有样本,期望损失为所有样本决策损失之和 -
朴素贝叶斯分类器
贝叶斯分类器:决策目标:最小化期望损失
如果特征是多维的,那么特征之间的相关性会导致学习困难
因此通过假设特征之间符合独立同分布简化计算,此即朴素贝叶斯分类器 -
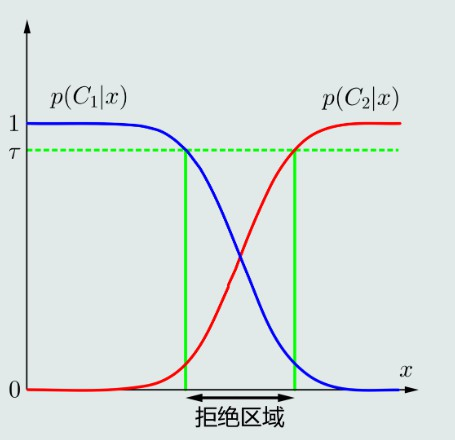
拒绝选项
MAP虽然是选择最大后验概率所属的类,但可能没比另一个类的概率高多少,例如在两个类别决策边界附近,这种决策并不确定
为了避免出现错误决策,就引入了拒绝选项,将这种情况划定为拒绝区域,拒绝分类
4、 最大似然估计
-
引言
在前述的贝叶斯决策中,求取后验概率需要事先知道每个类的先验概率和似然概率,这两个概率分布需要通过机器学习算法得到 -
监督式学习方法
参数化方法:给定概率分布的解析表达,学习这些解析表达函数中的参数。比如假定分布服从高斯分布,就可以通过学习确定高斯分布的均值与方差,从而确定该分布。常用方法为最大似然估计和贝叶斯估计 -
费参数化方法:概率密度函数形式未知,基于概率密度估计技术,估计非参数化的概率密度表达
-
最大似然估计
待学习的概率密度函数记作p(x|θ),θ是待学习的参数,代表在θ下取到x的概率,是样本数据x的分布
从p(x|θ)采样N个符合iid条件(独立同分布)的训练样本,则所有样本联合概率密度为 L = p(x1, x2, ..., xn|θ) = ∏p(xi|θ),此即似然函数
极大似然估计就是在θ所有取值中试图找到一个能使数据出现概率最大的值,即 θ^ML=\argmaxθ∏Nn=1p(xn∣θ),表示参数θ能最大化拟合样本数据x
观测概率估计:高斯分布
假定观测似然概率(p(x|θ))服从高斯分布,即 p(x|μ,Σ)=12π√Σe−(x−μ)22Σ2,此时θ为高斯分布的μ,Σ
则Ci类(!注意,仅表示其中一个类)的似然函数就变为p(x1,x2,…,xNi∣μ,Σ)=∏Nin=11(2π)p2|Σ|1/2e−12(xn−μ)TΣ−1(xn−μ)
对上述Ci类的似然函数取对数,这可以防止概率连乘造成的下溢。再分别对μ与∑求偏导,并令导数为0...(经过复杂的运算)...最后可解出:
μ^ML=1N∑N1n=1xn
,即高斯分布的均值的最大似然估计等于所有样本的均值
ΣML=1N∑N1n=1(xn−μ)(xn−μ^)T,高斯分布的协方差的最大似然估计等于所有所有样本的协方差
5、 最大似然的估计偏差
-
无偏估计
参数的估计量的数学期望是该参数的真值,则该股计量称作无偏估计,它意味着只要训练样本足够多,该估计值就是参数的真实值 -
高斯均值/协方差
求取E[μ^ML]=…=μ,故均值的最大似然估计是无偏估计
同理求取E[Σ^ML]=…!=Σ,故协方差的最大似然估计是有偏估计 -
高斯协方差估计偏差
协方差估计偏差为1NΣ,是一个较小的数,实际计算可以将训练样本的协方差乘以NN−1来修正协方差的估计值
3.6 贝叶斯估计(1) -估计θ的后验概率
- 定义
贝叶斯估计:给定参数θ分布的先验概率p(θ)和训练样本,估计参数θ分布的后验概率
与最大似然估计MLP还是MAP不同,贝叶斯估计不直接估计参数θ的值,而是允许参数θ服从一定概率分布,然后求出θ的期望值作为其最终值
先验概率反映了关于θ的最初猜测及其不确定信息
- 参数的后验概率
给定单个Ci类的训练样本集合Di,针对θ应用贝叶斯理论,由于p(Di)是与θ无关的数,可记作1/α,根据iid条件得到其后验概率:
p(θ∣Di)=p(θ∣{xn})=α∏Nin=1p(xn∣θ)p(θ)∗1
假设Ci类观测似然概率是单维高斯分布,且方差σ**2已知,则θ只是高斯分布的均值
p(xn∣θ)=N(θ, σ2)∗2
假设θ的先验概率分布也服从单维高斯分布,且该分布的均值和方差(因为单维所以这里是方差而非协方差)已知
p(θ)=N(μ0, σ20)∗3
带入上述2、3到1,可得p(θ∣{xn})表达式,记作4,(太复杂不想写了)
*4展开,省略与θ无关项后可改写成高斯分布的形式(均值和方差记作μθ和σθ)
p(θ∣{xn})=12π√σθe−(θ−μθ)22σ2θ∗5
对比4与5,主要看θ的平方和一次方项的系数,于是可以解出参数μθ和σ2θ,记作*6,这样就得到了θ的后验概率,它是一个高斯分布,均值和方差为μθ和σθ
观察*6,若先验方差σ0=0,意味先验确定性大,先验均值影响大,后续训练样本的进入对参数估计没有太多改变
若σ0≫θ,意味先验确定性非常小。刚开始由于样本小估计不准,但随着样本增加,后验均值回避金样本均值
- 总结
当训练样本个数Ni非常大时,limμθ=m,limσ2θ=0,样本均值m就是θ的无偏估计
贝叶斯估计具有不断学习的能力,它允许最初的、基于少量训练样本的、不太准确的估计,随着样本个数的增加,可以串行地不断修正参数估计值,从而达到该参数的期望真值
7、 贝叶斯估计(2) -估计观测似然关于θ的边缘概率
- 利用θ的后验概率
给定单个Ci类的训练样本集合Di,由于θ取值很多,这里求θ的边缘概率(对θ求积分),进一步表达出P(x|Di):
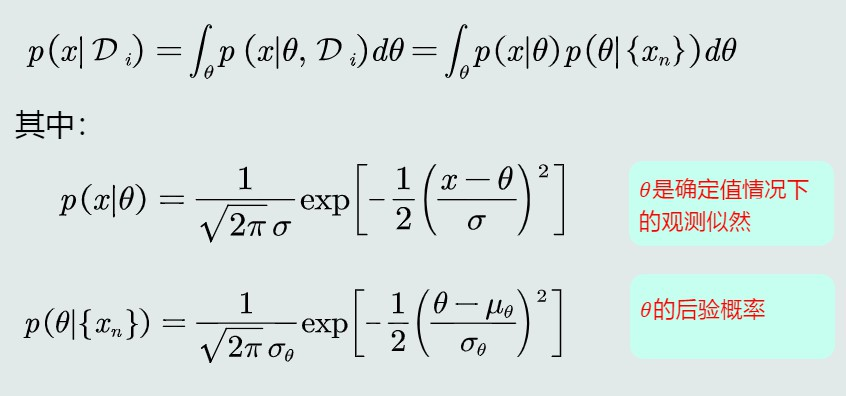
带入后分成与θ相关或不相关的两部分,整理后发现观测似然概率可以看做是关于x的高斯分布:
p(x∣Di)=N(μθ, σ2+σ2θ)
- 贝叶斯估计vs
把参数看作参数空间的一个概率分布
贝叶斯估计依赖训练样本来估计参数的后验概率,从而得到观测似然函数的边缘概率: p(x∣Di)
这个边缘概率就是分类器最后要用到的观测似然概率
观察其表达式,σ2θ代表了对于未知均值μ的不确定性,随着样本个数增大,μθ趋近真实均值m。此时p(x∣Di)→N(μ, σ2),趋近于假设的真实的观测似然的分布
vs最大似然估计
把观测似然的参数θ看作确定值,即参数空间一个固定的点
最大似然估计有明确的目标函数,通过优化技术可以直接求取θML,即求偏导就可得到估计值
而在贝叶斯估计里θ有多种取值的可能性,要先求θ的边缘概率才能得到观测似然,计算复杂度更高
8、 KNN估计
-
引言
之前讲的贝叶斯估计等都是假设概率分布为高斯分布,但如果分布未知,就需要使用无参数估计技术来实现概率密度估计
常用的无参数估计技术:KNN、直方图、核密度,皆基于p(x)=kNV去估计概率密度 -
KNN估计概念
K近邻估计,给定N个训练样本和k值,以待分类的样本x为中心,由内向外找到区域R,R里面包含k个训练样本,第k个样本与x距离记作dk(x),则区域R的体积V=2dk(x)
概率密度估计表达为:p(x)≈k2Ndk(x)
当训练样本个数N越大,k取值越大,概率估计越准确 -
KNN估计特点
优点:
根据训练样本分布的疏密情况,自适应确定区域R的范围
缺点:
KNN估计不是连续函数
也不是真正的概率密度表达,概率密度函数积分为∞而非1
推理测试阶段(训练完投入使用后)仍需要存储所有测试样本
易受噪声影响
- KNN分类器
基于MAP分类器,假设每个类的观测似然函数基于KNN估计
(利用先验后验概率、观测似然等进行理论推导...)
=>
以测试样本x为中心出发找到与其距离最近的k个样本,这k个里占比最大的类别就作为x的类别
9、 直方图与核密度估计
引言
KNN需要存储所有测试样本,且易受噪声影响
=>使用其他方法
-
直方图估计概念
将特征空间划分为m个格子(bins),每个格子就是一个区域R,即区域的位置固定、大小固定,而k值不需要给定,与KNN相反。
概率密度估计表达为:p(x)=kmNh, if x∈bm
其中bm是第m个格子的名字,km是第m个格子里的样本数
可见直方图估计也不是连续的 -
直方图估计特点
优点:
固定区域R:减少噪声污染造成的估计误差
不需要存储训练样本
缺点:
固定R的位置:若x在相邻格子交界处,则当前格子不是以x为中心,导致统计和概率估计不准确
固定R的大小:缺乏概率估计的自适应能力,导致过于尖锐或平滑
直方图统计阶段:双线性插值
针对手动确定R导致R的位置固定,自适应能力不强的问题而提出
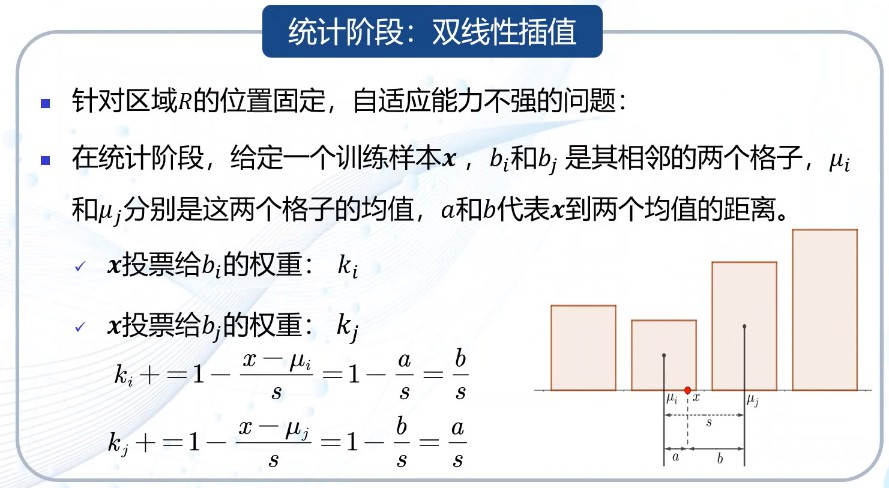
此时x并不是固定属于某个格子,而是按权重分属这两个格子,这两个格子的统计值ki、kj相应增加一定比例的x
虽然应用了双线性插值,但自适应能力仍然缺乏
- 核密度估计概念
为了解决knn已被噪声污染、直方图估计缺乏自适应能努力的问题
自适应R:以任意带估计样本x为中心,固定带宽h,依次确定一个区域R
定义一个窗口函数,以u=x−xnh 为中心的单位超立方体
窗口函数可写成一个核函数:K(x∣xn, h)=K(x−xnh)
训练样本落入R则核函数输出为1,否则为0
落入区域R的训练样本总数:k=∑Nn=1K(x∣xn, h)
概率密度估计表达为:p(x)=1NV∑Nn=1K(x∣xn, h)
核函数
核函数必须是对称函数
核函数可以是高斯分布、均匀分布、三角分布等
如果基于高斯核函数,则估计的概率密度是连续的
- 核密度估计特点
优点:
以x为中心,自适应确定R的位置(类似KNN)
使用所有训练样本,不是基于第k个近邻点来估计概率密度,没有KNN的噪声问题
若选取连续的核函数,则估计的概率密度也是连续的
缺点:
和直方图估计相比,核密度估计不提前根据训练样本估计每个格子统计值,仍然需要存储所有训练样本
带宽选择
原则:泛化能力
带宽h决定了估计概率的平滑程度,根据训练样本估计出来的概率分布要具有泛化能力
vs直方图
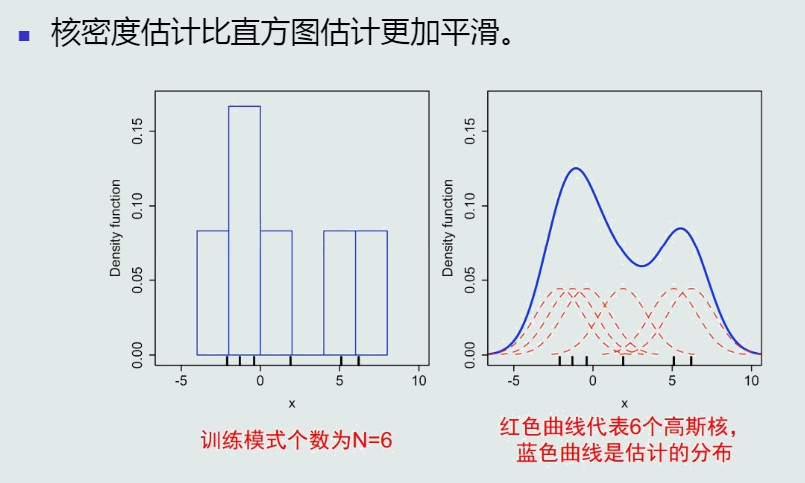
核密度估计比直方图估计更加平滑


 浙公网安备 33010602011771号
浙公网安备 33010602011771号