嫁不嫁问题让你通俗易懂的了解朴素贝叶斯分类
概述
贝叶斯分类算法是统计学的一种概率分类方法,朴素贝叶斯分类是贝叶斯分类中最简单的一种。其分类原理就是利 用贝叶斯公式根据某特征的先验概率计算出其后验概率,然后选择具有最大后验概率的类作为该特征所属的类。之 所以称之为”朴素”,是因为贝叶斯分类只做最原始、最简单的假设:所有的特征之间是统计独立的。
1.条件概率公式
条件概率(Condittional probability),就是指在事件B发生的情况下,事件A发生的概率,用P(A|B)来表示。
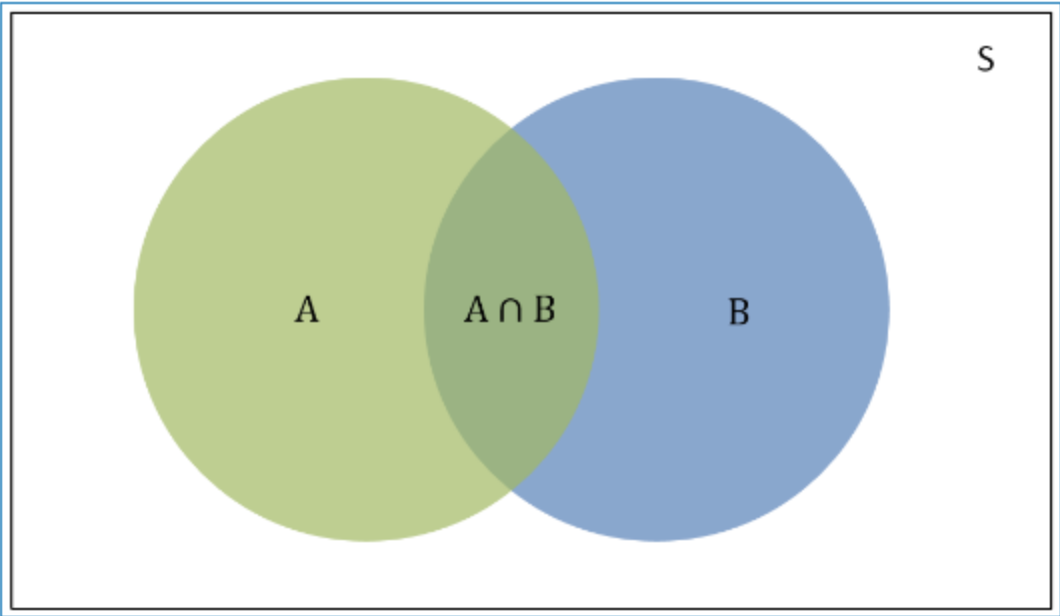
根据文氏图可知:在事件B发生的情况下,事件A发生的概率就是P(A∩B)除以P(B)。
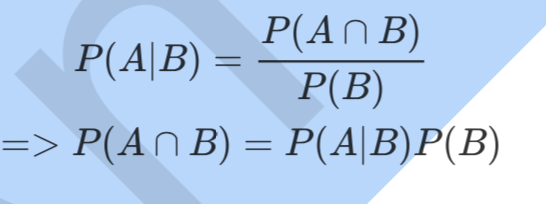

同理可得:

所以

全概率公式:如果事件 构成一个完备事件且都有正概率,那么对于任意一个事件B则 有:
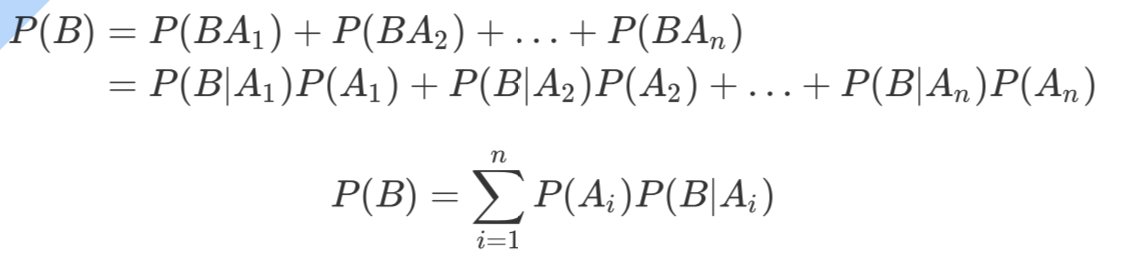
2.贝叶斯推断
根据条件概率和全概率公式,可以得到贝叶斯公式如下 :
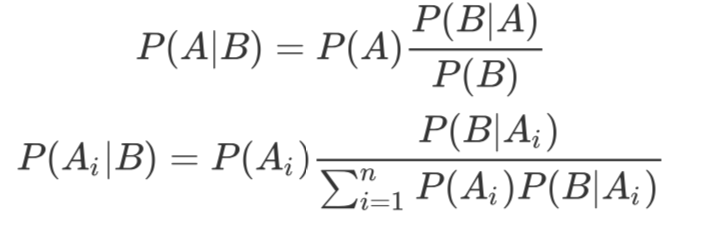
P(A)称为"先验概率”(Prior probability),即在B事件发生之前,我们对A事件概率的一个判断。
P(A| B)称为"后验概率" (Posterior probability),即在B事件发生之后,我们对A事件概率的重新评估。
P(B |A)/P(B)称为"可能性函数”(Likely hood), 这是一个调整因子,使得预估概率更接近真实概率。
所以条件概率可以理解为:后验概率=先验概率*调整因子
如果”可能性函数">1,意味着"先验概率"被增强,事件A的发生的可能性变大;
如果"可能性函数"=1,意味着B事件无助于判断事件A的可能性;
如果”可能性函数"<1,意味着"先验概率"被削弱,事件A的可能性变小。

3.案例分析(帅,高,上进,性格好,嫁不嫁问题?。。。)
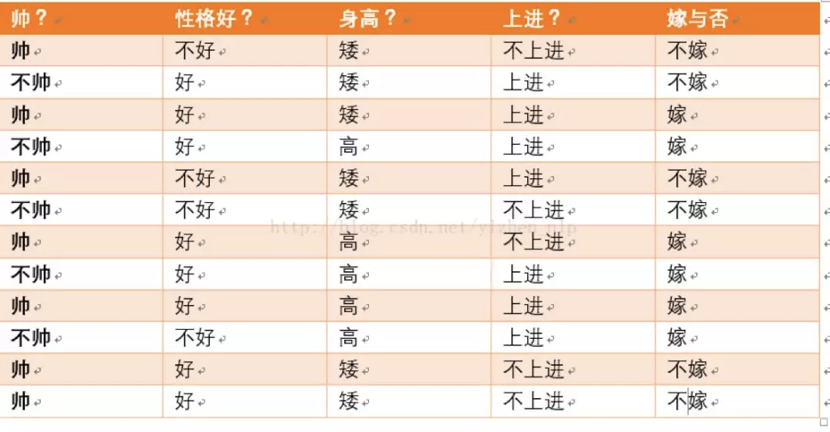
假如:不帅,性格不好,个子矮,不上进的男生,女生选择嫁的概率是多少?
即求出:
P(嫁|不帅, 性格不好,不高,不上进)
根据贝叶斯定理,拆成了三个概率的问题
1.P1=P(不帅,性格不好,不高,不上进|嫁)=P(嫁)*P(不帅|嫁)*P(性格不好|嫁)*P(不高|
嫁)*P(不上进|嫁)
2.P(嫁)
3.P2=P (不帅,性格不好,不高,不上进) =P(不帅)*P(性格不好)*P(矮)*P(不上进)
结果: P(嫁|不帅, 性格不好,不高,不上进)=P1*P(嫁)/P2
5.案例代码实现
生成样本(两个方法:随机生成,静态手动插入,选其一即可)
1 # 方法1,随机生成样本 2 import random 3 def create_Data1(): 4 looks=['帅','不帅'] 5 characters=['好','不好'] #性格 6 heights=['高','矮'] 7 progress=['上进','不上进'] 8 marriages=['嫁','不嫁'] 9 datasets=[] 10 for i in range(0,20): 11 dataset = []#创建样本 12 dataset.append(random.choice(looks)) #每个样本随机选择长相 13 dataset.append(random.choice(characters))#每个样本随机选择性格 14 dataset.append(random.choice(heights)) #每个样本随机选择高矮 15 dataset.append(random.choice(progress))#每个样本随机选择上不上进 16 dataset.append(random.choice(marriages))#每个样本随机选择嫁不嫁 17 print(dataset) 18 datasets.append(dataset)#将每一组样本加入到样本集中 19 print(datasets) 20 return datasets
1 # 方法2 指定数据样本 2 import random 3 def create_Data(): 4 datasets=[ 5 ['帅','不好','矮','不上进','不嫁'], 6 ['不帅','好','矮','上进','不嫁'], 7 ['帅','好','矮','上进','嫁'], 8 ['不帅','好','高','上进','嫁'], 9 ['帅','不好','矮','上进','不嫁'], 10 ['不帅','不好','矮','不上进','不嫁'], 11 ['帅','好','高','不上进','嫁'], 12 ['不帅','好','高','上进','嫁'], 13 ['帅','好','高','上进','嫁'], 14 ['不帅','不好','高','上进','嫁'], 15 ['帅','好','矮','不上进','不嫁'], 16 ['帅','好','矮','不上进','不嫁'] 17 ] 18 return datasets
1 # 计算函数 2 def compute_threeProb(datasets,c1,c2,c3,c4,c5):# 传入训练数据集,需要判断的数据(帅不帅,性格好不好,高还是矮,上不上进,嫁不嫁) 3 C5_count=0 #满足c5条件的数据条数 4 Result_count=0 #满足c5条件下且满足需要判断的四个特征的个数 5 p3_count=0 #计算样本中符合要判断的四个特征的个数 6 Allcount=len(datasets) #数据样本条数 7 for dataset in datasets: 8 #满足c5条件的数据条数 9 if dataset[4]==c5: 10 C5_count+=1 11 #该类别下满足需要判断的四个特征的个数 12 if dataset[0]==c1 and dataset[1]== c2 and dataset[2]==c3 and dataset[3]==c4: 13 Result_count+=1 14 #计算样本中符合要判断的四个特征的个数 15 if dataset[0] == c1 and dataset[1] == c2 and dataset[2] == c3 and dataset[3] == c4: 16 p3_count+=1 17 18 p1=(C5_count/Allcount)*(Result_count/C5_count) #类似 P(不帅,性格不好,不高,不上进|嫁) 19 p2=C5_count/Allcount #类似 P(嫁) 20 p3=p3_count/Allcount #类似 P(不帅,性格不好,不高,不上进) 21 if p3!=0: 22 prob_marriage=p1*p2/p3 23 print(prob_marriage) 24 return prob_marriage 25 else: 26 print("不存在!") 27 return 0
1 # 调用 2 datasets=create_Data() 3 rel=compute_threeProb(datasets,c1='帅',c2='好',c3='矮',c4='上进',c5='嫁') 4 print(f'此情况嫁的概率为:{rel}')
运行结果:

6.优缺点:
优点:
(1) 算法逻辑简单,易于实现(算法思路很简单,只要使用贝叶斯公式转化即可!)
(2)分类过程中时空开销小(假设特征相互独立,只会涉及到二维存储)
缺点:
(1)理论上,朴素贝叶斯模型与其他分类方法相比具有最小的误差率,但是实际上并非总是如此,
这是因为朴素贝叶斯模型假设属性之间相互独立,这个假设在实际应用中往往是不成立的,在
属性个数比较多或者属性之间相关性较大时,分类效果不好。
(2)在属性相关性较小时,朴素贝叶斯性能最为良好,对于这一点,有半朴素贝叶斯之类的算法
通过考虑部分关联性适度改进。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号