软件工程基础 第3次个人作业

一点说明

这篇博客是软件工程基础（罗杰、任建）的第三次课程作业（个人项目作业）

项目 内容
这个作业属于哪个课程 软件工程基础（罗杰，任建）
这个作业的要求在哪里 作业要求的链接
我在这个课程的目标是 提升对软件工程的宏观和微观的全面认识，并加以实践
作业在哪些方面帮我实现目标 亲身实践个人项目开发的完整流程
我的教学班级 006
我的GitHub项目地址 https://github.com/SnowOnVolcano/IntersectProject.git

PSP表格

在开始实现程序之前，在下述 PSP 表格记录下你估计将在程序的各个模块的开发上耗费的时间。（0.5'）

在你实现完程序之后，在下述 PSP 表格记录下你在程序的各个模块上实际花费的时间。（0.5'）

PSP2.1 Personal Software Process Stages 预估耗时（分钟） 实际耗时（分钟）
Planning 计划 15 20
· Estimate · 估计这个任务需要多少时间 15 20
Development 开发 330 470
· Analysis · 需求分析 (包括学习新技术) 60 80
· Design Spec · 生成设计文档 30 20
· Design Review · 设计复审 (和同事审核设计文档) 0 0
· Coding Standard · 代码规范 (为目前的开发制定合适的规范) 10 10
· Design · 具体设计 40 60
· Coding · 具体编码 100 120
· Test · 测试（自我测试，修改代码，提交修改 90 180
Reporting 报告 75 110
· Test Report · 测试报告 45 60
· Size Measurement · 计算工作量 10 10
· Postmortem & Process Improvement Plan · 事后总结, 并提出过程改进计划 20 40
Total 合计 420 600

基本需求

1. 解题思路

解题思路描述。即刚开始拿到题目后，如何思考，如何找资料的过程。（3'）

  • 思路一

    读完问题的第一思路，是利用高中学到的 一般方程法 进行交点的求解：

    \[设直线方程为\ ax+by+c=0，\ 已知直线过两点(x_1,y_1)和(x_2,y_2)，则有\\ \begin{cases}ax_1+by_1+c=0\\ax_2+by_2+c=0\end{cases}\implies \begin{cases}a=y_1-y_2\\b=x_2-x_1\\c=x_1y_2-x_2y_1\end{cases}\\ 设两直线分别为\ a_1x+b_1y+c_1=0\ 和\ a_2x+b_2y+c_2=0，联立两直线方程，得\\ \begin{cases}a_1x+b_1y+c_1=0\\a_2x+b_2y+c_2=0\end{cases}\implies \begin{cases}x=\frac{b_1c_2-b_2c_1}{a_1b_2-a_2b_1}\\y=\frac{a_2c_1-a_1c_2}{a_1b_2-a_2b_1}\end{cases}\implies \begin{cases}x=\frac{b_1c_2-b_2c_1}{D}\\y=\frac{a_2c_1-a_1c_2}{D}\end{cases}，其中\ D=a_1b_2-a_2b_1 \]

    这样的解法有几个好处：

    • 可以较好地处理特殊情况，比如，可以通过判断 D 是否为 0，直接判断两直线是否平行；
    • 这种方法直接计算出交点的坐标，这样可以设置一个 set 用来存放已得到的交点，直接在存入时进行除重，最终结果输出 set 的大小即可；

    当然，其缺点也很明显：

    • 计算简单粗暴，对于具有 N 条直线的样本，需要进行 \(C_N^2\) 次计算，时间复杂度为 \(O(n^2)\)；
    • 如果简单地使用 set<(x,y)> 进行的方式进行存储，则需要进行浮点运算，这既会带来精度的损失，也会加长运行时间。
  • 思路二

    如果不采用直接计算的方法，如何得出交点个数呢？我想到的另一个方法是，做减法。

    如果任意的两条直线都相交且任意的三条直线不交于同一点，那么对于具有 N 条直线的样本，交点的个数为 \(C_N^2\)，对一般情况就有，

    \[总交点数=C_N^2-平行直线对的数目-\sum_{所有的交点}{(同一交点的直线数目-2)} \]

    但是，仔细想想，这种方法似乎并不比思路简单，因为我没有想到好的算法去计算同一交点的直线数目……

  • 思路三

    想不到好的算法，我最后只能决定使用直接计算的方法，但是我想其实思路一的方法还可以简单地优化一下细节，减小精度损失，有两个方法，

    • 在存放交点时，交点的纵横坐标的分子分母分开存储，这样可以规避浮点运算，从而保证精度；
    • 对 set 的排序函数进行重载，设置一定的精度范围，这样可以一定程度地减小精度损失，但是无法从根本上避免。

    我最终选择了后者，以平衡精度和时间复杂度。

2. 实现过程

设计实现过程。设计包括代码如何组织，比如会有几个类，几个函数，他们之间关系如何，关键函数是否需要画出流程图？单元测试是怎么设计的？（4'）

  • 结构设计（2个结构体）
    • Point：表示点 \((x,y)\)，其中 Point.x、Point.y 分别表示点的纵横坐标；
    • Line：表示直线 \(ax+by+c=0\)，其中 Line.a、Line.b、Line.c 分别对应直线的三个参数；
  • 函数实现（2+1+1个函数）

    • Point 和 Line 的构造函数，计算两直线交点的函数 calLineLineIst(...) ，主函数；

    • 各函数关系如下，

      img
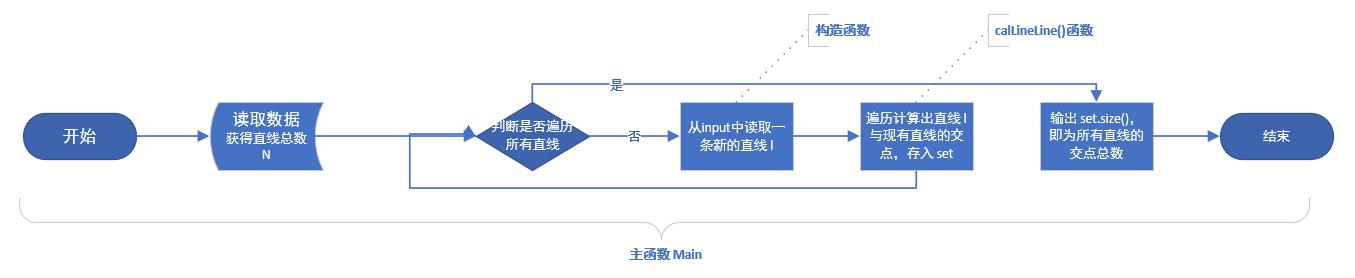
  • 单元测试

    我主要进行了三个方面的单元测试：

    • 构造函数是否能正确初始化：包括参数的传递和计算；
    • 交点计算函数是否能覆盖所有情况：包括多线一点、平行的情况，以及直线与坐标轴平行等情况；
    • 交点集合的精确度是否能保证：重点测试了以下两种情况，1）在交点相差较小的情况下，是否能够区分开不同的交点；2）在交点的小数点位数较多时，是否能保证交点不重复。

    以下是我的一些单元测试的测试点的图形示意：

3. 性能改进

记录在改进程序性能上所花费的时间，描述你改进的思路，并展示一张性能分析图（由 VS 2019 的性能分析工具自动生成），并展示你程序中消耗最大的函数。（3'）

  • 在改进之前，我进行了一次程序性能的测试，我发现，最费时的操作是 set 的插入时，遍历红黑树的过程。反而计算交点的函数没有花费太多的时间。
  • 但是，在尝试了非红黑树的集合之后，我发现有时候正确性得不到保证，所以我最后还是选择了保持原有的 set。
  • 其他的优化都是小修小补了，比如，
    • 优化了代码结构，将点和直线的初始化函数放入了结构体内；
    • 除了最后的计算，中间过程使用整型，而非浮点型
  • 优化后的图如下
img
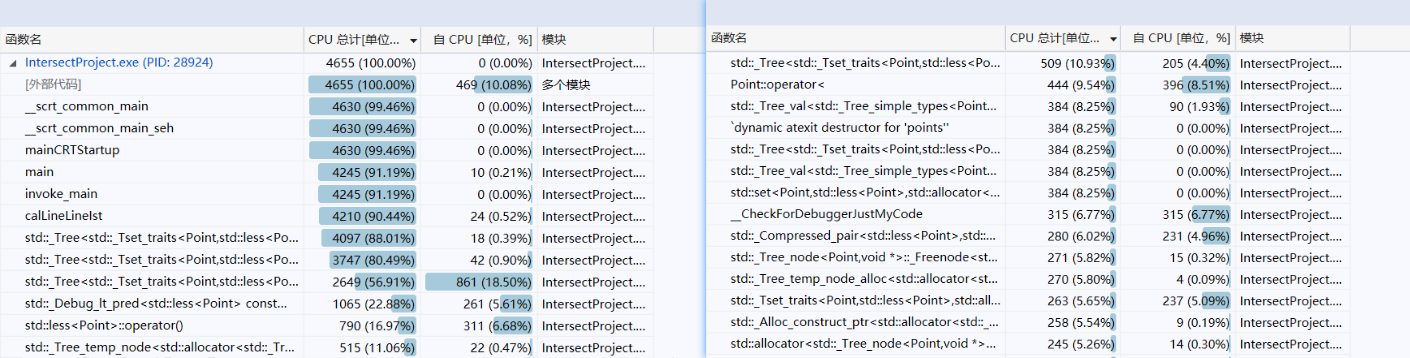
  • 程序中消耗最大的函数如下
img

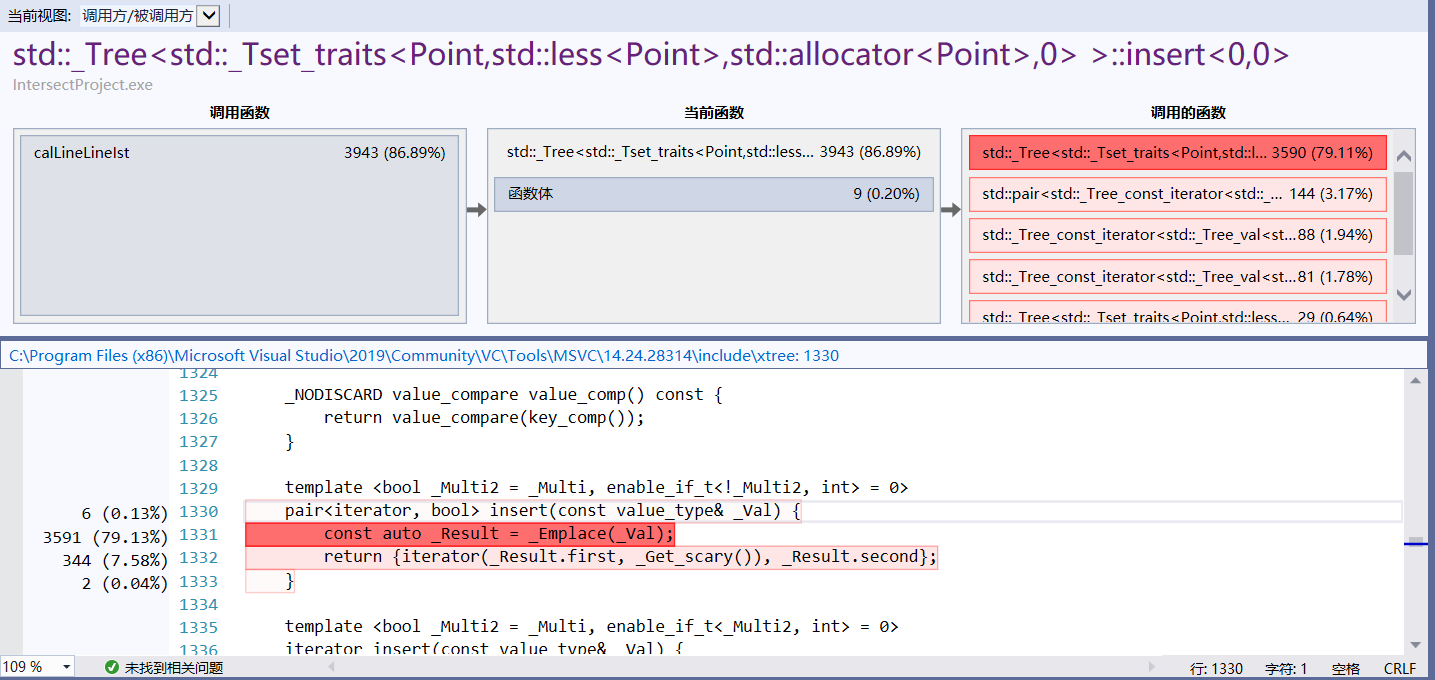
4. 代码说明

代码说明。展示出项目关键代码，并解释思路与注释说明。（3'）

  • 计算直线与直线交点（思路请见代码注释）
    // calculate the intersections of two lines
static void calLineLineIst(Line& line1, Line& line2) {
	int D；
    D = line1.a * line2.b - line2.a * line1.b;
	switch (D)
	{
	case 0:	// parallel
		break;
	default:
		//	line1: a1*x+b1*x+c1=0, line2: a2*x+b2*x+c2=0
		//	==> x=(b1*c2-b2*c1)/(a1*b2-a2*b1),
		//		y=(a2*c1-a1*c2)/(a1*b2-a2*b1)
		//	let D=a1*b2-a2*b1
		//	==> x=(b1*c2-b2*c1)/D, y=(a2*c1-a1*c2)/D
		Point point = { 
			(line1.b * line2.c - line2.b * line1.c) / (float)D, 
			(line2.a * line1.c - line1.a * line2.c) / (float)D 
		};
		points.insert(point);
		break;
	}
}

  • 集合的排序和精度的确定

    bool operator == (const Point& other) const {
	return fabs(x - other.x) < 0.00000001 && fabs(y - other.y) < 0.00000001;
	}
bool operator < (const Point& other) const {
	if (x != other.x) {
		return x < other.x;
	}
	else {
		return y < other.y;
	}
}

附加题

1. 解题思路

\[已知两圆\ (x-x_1)^2+(y-y_1)^2=(r_1)^2\ 和\ (x-x_2)^2+(y-y_2)^2=(r_2)^2\ ，\\设圆心距为\ d，则有\ \ \ \begin{cases}两圆内含或相离， &d<|r_1-r_2|\ 或\ d>r_1+r_2\\两圆相交或相切，&|r_1-r_2|\leq d\leq r_1+r_2\end{cases}\\\begin{cases}(x-x_1)^2+(y-y_1)^2=(r_1)^2\\(x-x_2)^2+(y-y_2)^2=(r_2)^2\end{cases}\implies 2(x_2-x_1)x+2(y_2-y_1)y+x_1^2-x_2^2+y_1^2-y_2^2+r_2^2-r_1^2\\\implies \begin{cases}(x-x_1)^2+(y-y_1)^2=(r_1)^2\\ 2(x_2-x_1)x+2(y_2-y_1)y+x_1^2-x_2^2+y_1^2-y_2^2+r_2^2-r_1^2\end{cases}\implies 求出交点坐标 \]

2. 代码说明

  • 计算直线与圆交点（思路请见代码注释）
    // calculate the intersections of line and Circle
static void calLineCircleIst(Line& line, Circle& circle) {
	int intercept;
	// intercept=r^2-d^2=r^2-(ax+by+c)^2/(a^2+b^2)
	intercept = (int)(pow(circle.r, 2) - pow(line.a * circle.x + line.b * circle.y + line.c, 2) / (pow(line.a, 2) + pow(line.b, 2)));
	// not intersect
	if (intercept < 0) { return; }
	// tLine is perpendicular to line
	Line tLine = { line.b, -line.a, line.a * circle.y - line.b * circle.x };
	int D;
	D = tLine.a * line.b - line.a * tLine.b;
	// tPoint is the intersection of line and tLine
	Point tPoint = {
		(tLine.b * line.c - line.b * tLine.c) / (float)D,
		(line.a * tLine.c - tLine.a* + line.c) / (float)D
	};
	switch (intercept) 
	{
	case 0:	// line is tangent to circle
		points.insert(tPoint);
		break;
	default:// line passes through circle
		float vecX;
		float vecY;
		float offset;
		// (vecX, vecY) is a unit vector
		vecX = (float)(line.b / sqrt(pow(line.a, 2) + pow(line.b, 2)));
		vecY = (float)(-line.a / sqrt(pow(line.a, 2) + pow(line.b, 2)));	
		// Offset is half of the intercept
		offset = (float)sqrt(intercept / (pow(line.a, 2) + pow(line.b, 2)));
		// intersection = tPoint +/- vec*offset
		Point ist1 = { tPoint.x + vecX * offset, tPoint.y + vecY * offset };
		Point ist2 = { tPoint.x - vecX * offset, tPoint.y - vecY * offset };
		points.insert(ist1);
		points.insert(ist2);
		break;
	}
}
  • 计算圆与圆交点（思路请见代码注释）
    // calculate intersections of two circles
static void calCircleCircleIst(Circle& circle1, Circle& circle2) {
	int radiusSum;
	int radiusDiff;
	int centerDis;
	radiusSum = (int)pow(circle1.r + circle2.r, 2);
	radiusDiff = (int)pow(circle1.r - circle2.r, 2);
	centerDis = (int)(pow(circle1.x - circle2.x, 2) + pow(circle1.y - circle2.y, 2));
	// not intersect
	if (centerDis > radiusSum || centerDis < radiusDiff) {
		return;
	}
	// line passes both two intersections of circles
	Line line = {
		circle1.d - circle2.d, 
		circle1.e - circle2.e,
		circle1.f - circle2.f
	};
	// the intersections of two circles are also the intersections of line and circle
	calLineCircleIst(line, circle1);
}

截图 - 测试与度量

1. 单元测试覆盖率

img

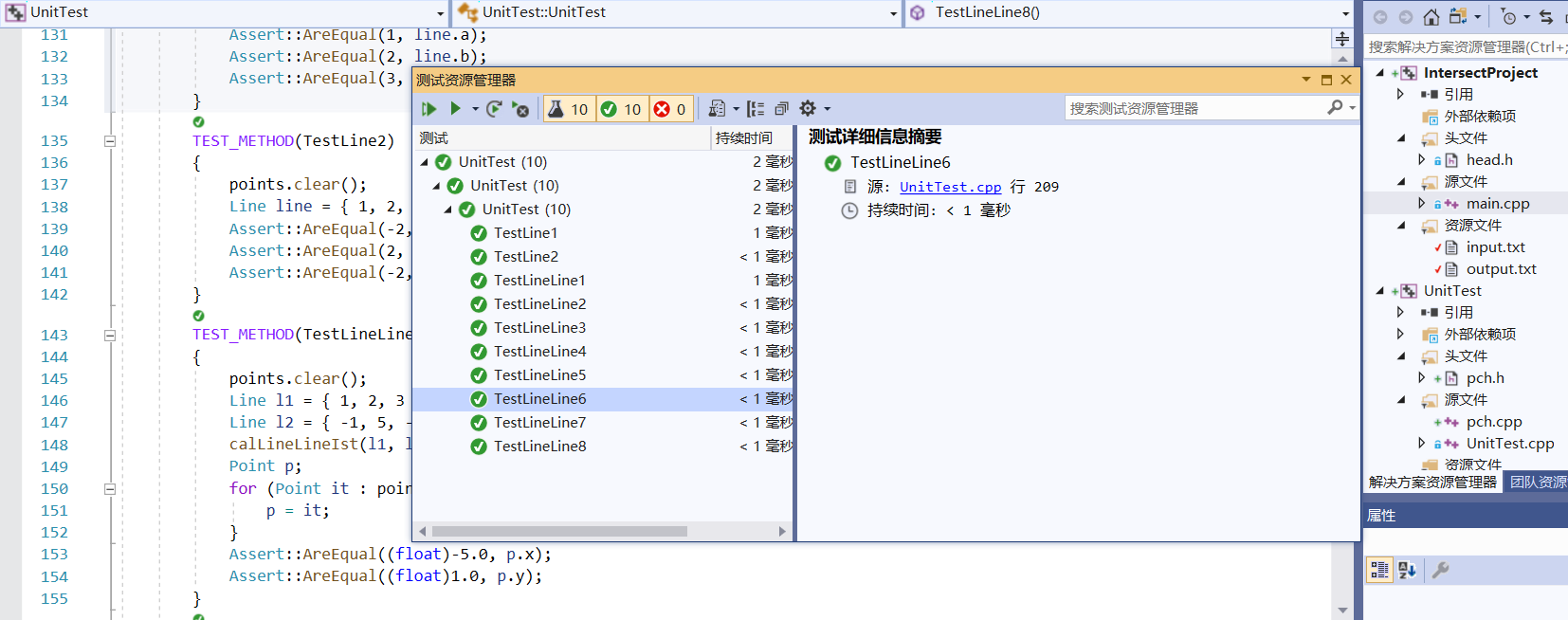
2. Code Quality Analysis 警告消除

img
posted @ 2020-03-10 16:07  FUJI_W  阅读(197)  评论(2)  编辑  收藏  举报